Tam giác ABC có: \(\widehat{BAC}=105\) độ, \(\widehat{ACB}=45\) độ, BC= 4cm. Tính AB, AC
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NH
Những câu hỏi liên quan
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE,AC = DF,\widehat {BAC} = \widehat {EDF} = {60^\circ },BC = 6\;{\rm{cm}},\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
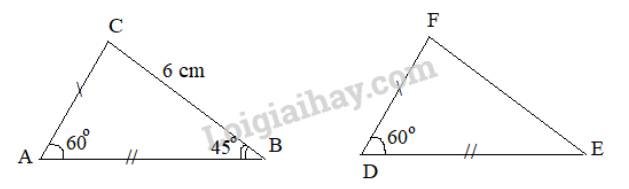
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(BC=EF = 6cm\) ( 2 cạnh tương ứng)
\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)
Đúng 0
Bình luận (0)
Tam giác ABC có \(\widehat{A}=105^0;\widehat{B}=45^0;CB=4cm\). Tính độ dài các cạnh AB, AC ?
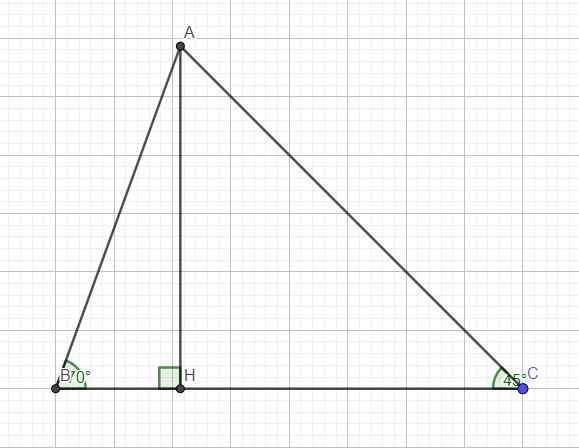
Cho tam giác ABC có BC = 4cm, \(\widehat{B}=70^o\), \(\widehat{C}=45^o\). Tính độ dài AC và diện tích tam giác ABC?
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Cho △ABC có \(\widehat{A}\)=45 độ, \(\widehat{B}\)=75 độ thì:
a. BC<AB<AC
b. BC<AC<AB
c. AB<AC<BC
d. AC<BC<AB
Xem thêm câu trả lời
\(\Delta ABC\) có \(\widehat{A}=105^0,\widehat{B}=45^0,BC=4cm\) . Tính độ dài cạnh AB, AC.
Cho tam giác ABC có AB = 4cm; AC = 5cm; BC = 6cm. Trên tia đối tia AB lấy D sao cho AD = 5cm.
a. Tam giác ABC đồng dạng với tam giác nào?
b. Tính CD.
c. CMR: \(\widehat{BAC}=2\widehat{ACB}\)
\(BD=AB+AD=4+5=9\left(cm\right)\)
\(\Delta ABC\) và \(\Delta CBD\) có:
\(\frac{AB}{BC}=\frac{BC}{BD}\left(=\frac{2}{3}\right)\)
Góc B chung
\(\Rightarrow\Delta ABC\infty\Delta CBD\left(c.g.c\right)\Rightarrow\hept{\begin{cases}\widehat{ACB}=\widehat{D}\\\frac{AB}{CB}=\frac{AC}{CD}\left(1\right)\end{cases}}\)
b, Từ (1) thay số vào: \(\frac{4}{6}=\frac{5}{CD}\Rightarrow CD=7,5\left(cm\right)\)
c, \(\widehat{BAC}=\widehat{D}+\widehat{ACD}=2\widehat{D}=2\widehat{ACB}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(AC=\sqrt{2};\widehat{BAC}=105^0;\widehat{ACB}=30^0\). Tính độ dài cạnh BC.
1.Cho tam giác ABC vuông tại A.Kẻ đường cao AH,biết AB=4cm,HC=6cm.Tính \(\widehat{B},\widehat{C}\) và AC
2.Cho tam giác ABC có \(\widehat{A}=105^o,\widehat{B}=45^o,BC=4cm\).Tính độ dài AB,AC
Câu 1:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+6\right)=16\)
=>BH=2(cm)
BC=BH+CH=8cm
\(AC=\sqrt{8^2-4^2}=4\sqrt{3}\left(cm\right)\)
sin B=AC/BC=căn 3/2
nên góc B=60 độ
=>góc C=30 độ
Đúng 0
Bình luận (0)
một cái thang xếp dạng hình tam giác ABC có chiều cao AH ;\(\widehat{ABC=60}\)độ ;\(\widehat{ACB}\)=45 độ. tính AB;AC;AH
biết khoảng cách 2 chân thang là 120cm