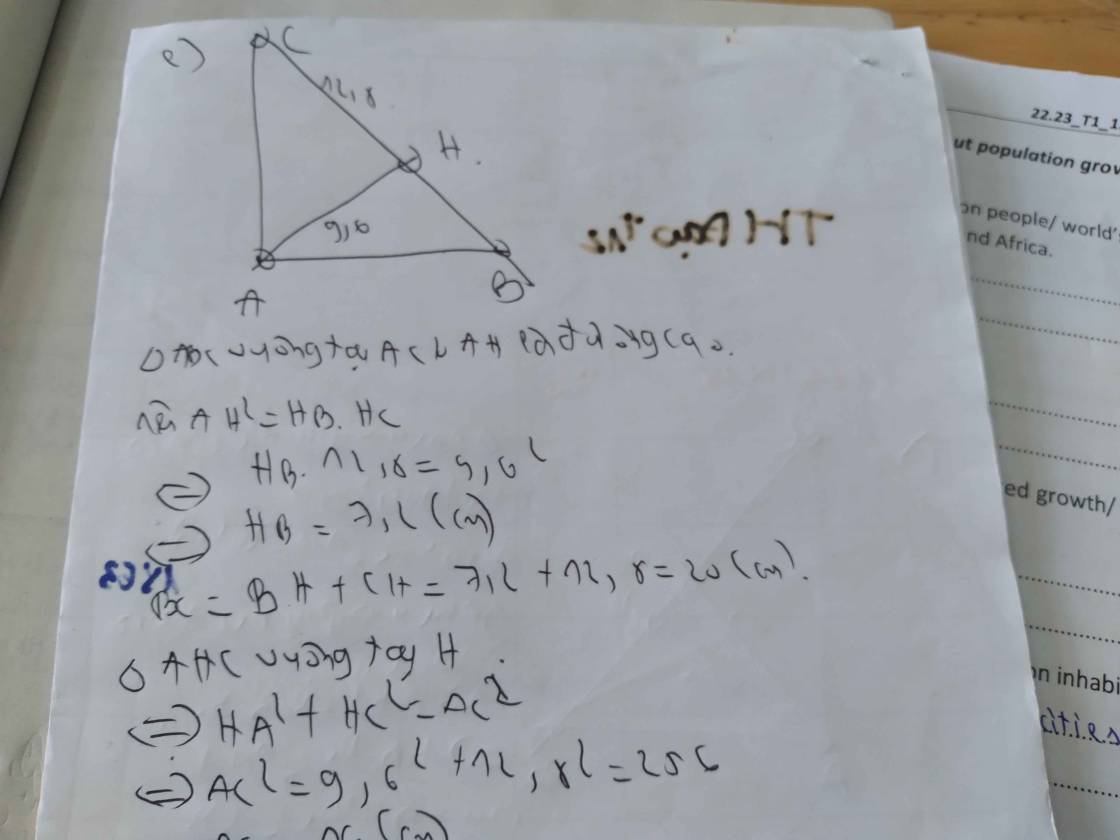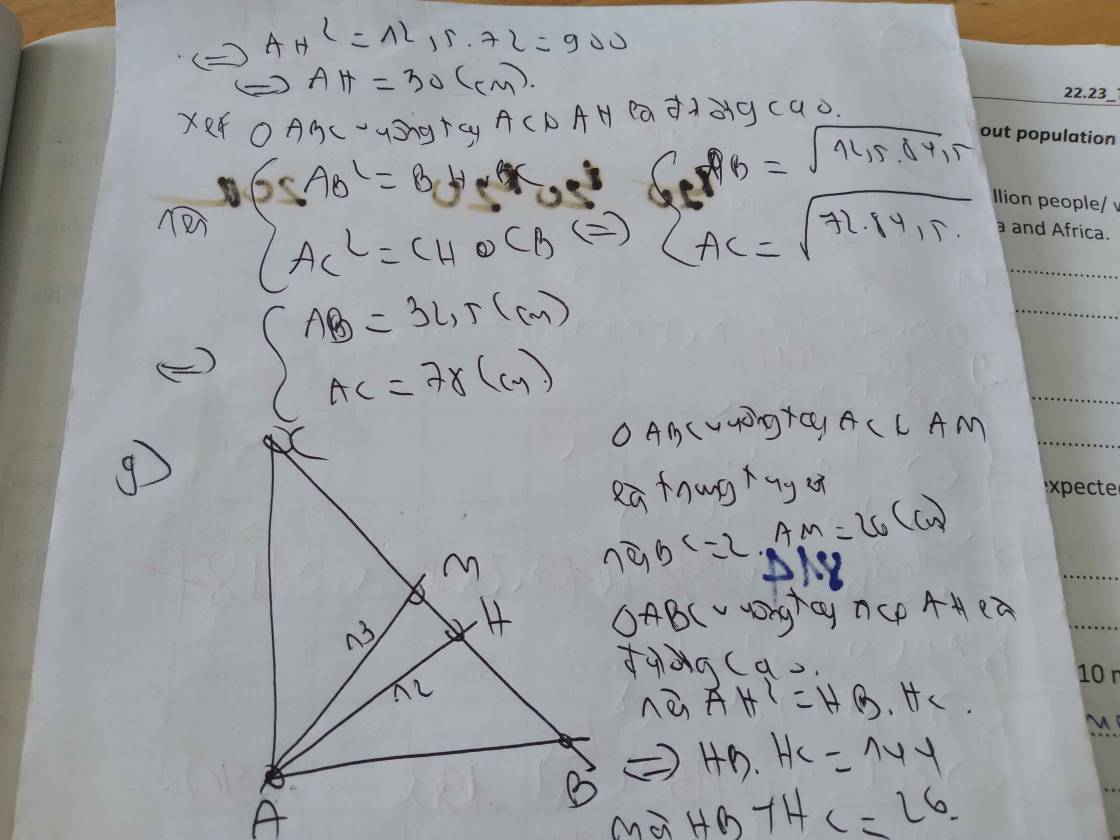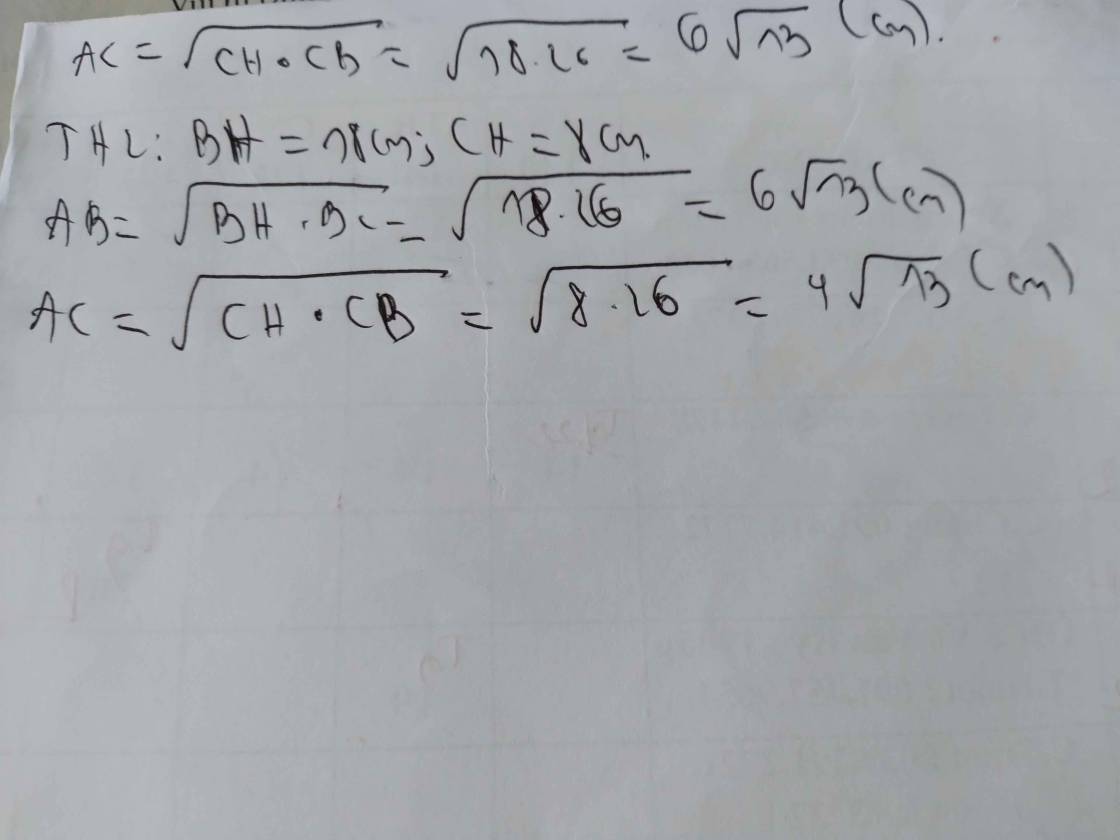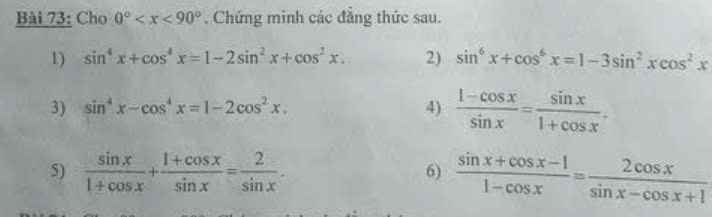
Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
1: \(sin^4x+cos^4x\)
\(=\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\)
\(=1-2\cdot sin^2x\cdot cos^2x\)
2: \(sin^6x+cos^6x\)
\(=\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)\)
\(=1-3\cdot sin^2x\cdot cos^2x\)
3: \(sin^4x-cos^4x\)
\(=\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)\)
\(=sin^2x-cos^2x\)
\(=1-cos^2x-cos^2x=1-2\cdot cos^2x\)
4: \(\left(1-cosx\right)\left(1+cosx\right)-sin^2x\)
\(=1-cos^2x-sin^2x\)
=1-1
=0
=>\(\left(1-cosx\right)\left(1+cosx\right)=sin^2x\)
=>\(\dfrac{1-cosx}{sinx}=\dfrac{sinx}{1+cosx}\)
5: \(\dfrac{sinx}{1+cosx}+\dfrac{1+cosx}{sinx}\)
\(=\dfrac{sin^2x+\left(1+cosx\right)^2}{sinx\left(1+cosx\right)}\)
\(=\dfrac{sin^2x+cos^2x+2\cdot cosx+1}{sinx\left(1+cosx\right)}\)
\(=\dfrac{2\cdot cosx+2}{sinx\left(1+cosx\right)}=\dfrac{2}{sinx}\)
6: \(\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)-2\cdot cosx\left(1-cosx\right)\)
\(=sin^2x-\left(cosx-1\right)^2-2cosx+2\cdot cos^2x\)
\(=sin^2x-\left(cos^2x-2\cdot cosx+1\right)-2\cdot cosx+2\cdot cos^2x\)
\(=sin^2x-cos^2x+2\cdot cosx-1-2\cdot cosx+2\cdot cos^2x\)
\(=sin^2x+cos^2x-1=1-1=0\)
=>\(\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)=2\cdot cosx\left(1-cosx\right)\)
=>\(\dfrac{sinx+cosx-1}{1-cosx}=\dfrac{2cosx}{sinx-cosx+1}\)
Đúng 1
Bình luận (0)
1) Ta có: \(sin^2x+cos^2x=1\Leftrightarrow\left(sin^2x+cos^2x\right)^2=1\)
\(\Leftrightarrow sin^4x+2sin^2x\cdot cos^2x+cos^4x=1\)
\(\Leftrightarrow sin^4x+cos^4x=1-2sin^2x\cdot cos^2x\)
P/s: Chắc là thừa mất dấu (+) ở vế phải chứ nếu nó có (+) thì ko đúng
2) Ta có: \(sin^2x+cos^2x=1\Leftrightarrow\left(sin^2x+cos^2x\right)^3=1\)
\(\Leftrightarrow sin^6x+cos^6x+3sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)=1\)
\(\Leftrightarrow sin^6x+cos^6x=1-3sin^2x\cdot cos^2x\)
3) Ta có: \(sin^4-cos^4x=sin^4x+cos^4x-2cos^4x\)
\(=1-2sin^2x\cdot cos^2x-2cos^4x\) (theo p1)
\(=1-2cos^2x\left(sin^2x+cos^2x\right)\)
\(=1-2cos^2x\)
4) Ta có: \(\dfrac{1-cosx}{sinx}=\dfrac{\left(1-cosx\right)\left(1+cosx\right)}{sinx\left(1+cosx\right)}=\dfrac{1-cos^2x}{sinx\left(1+cosx\right)}=\dfrac{sin^2x}{sinx\left(1+cosx\right)}=\dfrac{sinx}{1+cosx}\)5) Ta có:
\(\dfrac{sinx}{1+cosx}+\dfrac{1+cosx}{sinx}=\dfrac{sin^2x+\left(1+cosx\right)^2}{sinx\left(1+cosx\right)}\)
\(=\dfrac{sin^2x+cos^2x+1+2cosx}{sinx\left(1+cosx\right)}\)
\(=\dfrac{2\left(1+cosx\right)}{sinx\left(1+cosx\right)}=\dfrac{2}{sinx}\)
6) \(\dfrac{sinx+cosx-1}{1-cosx}=\dfrac{\left(sinx+cosx-1\right)\left(sinx+cosx+1\right)}{\left(1-cosx\right)\left(sinx+cosx+1\right)}\)
\(=\dfrac{\left(sinx+cosx\right)^2-1}{sinx+cosx+1-sinx\cdot cosx-cos^2x-cosx}\)
\(=\dfrac{sin^2x+cos^2x+2sinx\cdot cosx-1}{sinx+sin^2x+cos^2x-sinx\cdot cosx-cos^2x}\)
\(=\dfrac{2sinx\cdot cosx}{sinx\left(sinx-cosx+1\right)}\)
\(=\dfrac{2cosx}{sinx-cosx+1}\)
Đúng 1
Bình luận (0)
BẠN NÀO LÀM ĐƯỢC CÂU NÀO THÌ LÀM THÔI NHA
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a đường ca hát maya 2m HC bằng 3cm độ dài BH là
Cho tam giác ABC vuông tại A (AB < AC), có đường cao AH (H thuộc BC)
a) Cho biết HB = 3cm, HC = 9cm. Tính AH, AB, AC?
b) Chứng minh: tan2C + cot2C = HC/HB + HC/HB (không sử dụng số liệu ở câu a để chứng minh).
Mình giải bài mà bí quá, SOS xin các thần thánh cao nhân cứu giúp!!!
a: BC=BH+CH
=3+9
=12(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=3\cdot9=27\)
=>\(AH=3\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{3\cdot12}=6\left(cm\right)\\AC=\sqrt{9\cdot12}=6\sqrt{3}\left(cm\right)\end{matrix}\right.\)
b: \(tan^2C+cot^2C\)
\(=\left(\dfrac{AC}{AB}\right)^2+\left(\dfrac{AB}{AC}\right)^2\)
\(=\dfrac{AC^2}{AB^2}+\dfrac{AB^2}{AC^2}\)
\(=\dfrac{HC\cdot BC}{HB\cdot BC}+\dfrac{HB\cdot BC}{HC\cdot CB}\)
\(=\dfrac{HC}{HB}+\dfrac{HB}{HC}\)
Đúng 0
Bình luận (0)
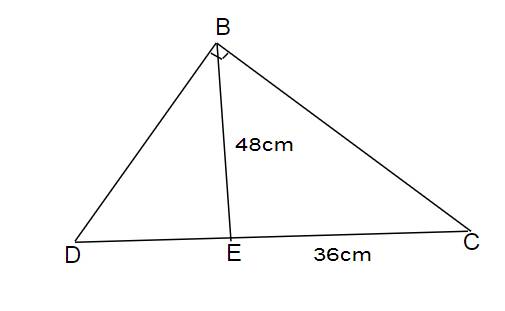
Cho tam giác BDC vuông tại B, đường cao BE. Biết CE = 36cm, BE = 48cm. Tính ED, BC và BD
`+,` Tính `ED`
Trong tam giác `BDC` vuông ta có hệ thức lượng :
`BE^2=ED* CE`
`48^2=ED*36`
`=> ED= (48^2)/36=64`
`+,` Tính `BC`
Ta có hệ thức lượng là :
`BC^2= DC*EC`
`= (64+36) * 36`
`= 3600`
\(\Rightarrow BC=\sqrt{3600}=60\)
`+,` Tính `BD`
Ta có hệ thức lượng là :
`BD^2= DC *ED`
`= 100 * 64`
`=6400`
\(\Rightarrow BD=\sqrt{6400}=80\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông cân tại B. Nếu AD=DC=3
Cho tam giác MNP vuông tại M , đg cao MH , có MN=6cm, NH=10cm.Tính MP, MH, NH, Hp
Sửa đề; NP=10cm
ΔMNP vuông tại M
=>\(MN^2+MP^2=NP^2\)
=>\(MP^2=10^2-6^2=64\)
=>MP=8(cm)
Xét ΔMNP vuông tại M có MH là đường cao
nên \(MH\cdot NP=MN\cdot MP\)
=>MH*10=6*8=48
=>MH=4,8(cm)
Xét ΔMNP vuông tại M có MH là đường cao
nên \(\left\{{}\begin{matrix}MN^2=NH\cdot NP\\PM^2=PH\cdot PN\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}NH=\dfrac{6^2}{10}=3,6\left(cm\right)\\PH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 8. Cho AABC vuông tại A có AB = 5cm; BC = 13cm; AH là đường cao. a) Tính AC, AH và B ( Số đo góc làm tròn đến độ, độ dài cạnh làm tròn đến chữ số thì phân thứ hai ). b) Gọi E, F lần lượt là hình chiếu của H trên AB, AC. Chứng minh AE.EB+AF.FC- HB.HC=0 c) Chứng minh AH=EF. Từ đó suy ra BC =3AH + BE +CF.
a) Ta có :
\(BC^2=AB^2+AC^2\left(Pitago\right)\)
\(\Leftrightarrow AC^2=BC^2-AB^2=169-25=144\)
\(\Leftrightarrow AC=12\left(cm\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{AB^2.+AC^2}{AB^2.AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{BC^2}{\left(AB.AC\right)^2}\)
\(\Leftrightarrow AH^2=\dfrac{\left(AB.AC\right)^2}{BC^2}=\dfrac{\left(5.12\right)^2}{13^2}\)
\(\Leftrightarrow AH=\dfrac{5.12}{13}=\dfrac{60}{13}\sim4,85\left(cm\right)\)
\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13}\Rightarrow\widehat{B}\sim67^o\)
Đúng 1
Bình luận (0)
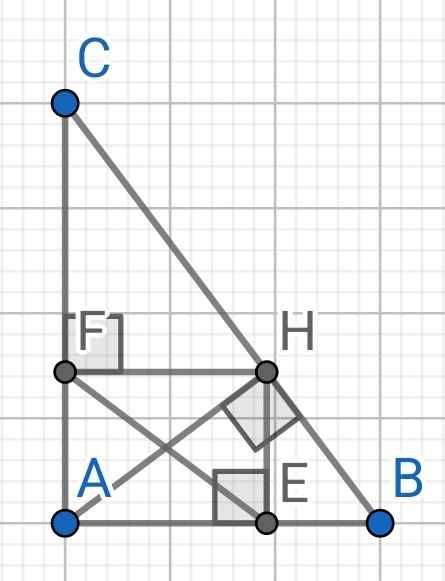 a) ∆ABC vuông tại A (gt)
a) ∆ABC vuông tại A (gt)
BC² = AB² + AC² (Pytago)A
⇒ AC² = BC² - AB²
= 13² - 5²
= 144
⇒ AC = 12 (cm)
Ta có:
AH.BC = AB.AC
⇒ AH = AB.AC : BC
= 5.12 : 13
= 60/13 (cm) ≈ 4,62 (cm)
sinB = AC/BC = 12/13
⇒ ∠B ≈ 67⁰
b) ∆AHB vuông tại H có HE là đường cao
⇒ HE² = AE . EB (1)
∆AHC vuông tại H có HF là đường cao
⇒ HF² = AF . FC (2)
Tứ giác AEHF có:
∠AEH = ∠EAF = ∠AFH = 90⁰
⇒ AEHF là hình chữ nhật
⇒ AH = EF
⇒ ∠EHF = 90⁰
∆EHF vuông tại H
⇒ EF² = HE² + HF²
⇒ AH² = HE² + HF²
Từ (1) và (2)
⇒ AE.EB + AF.FC = HE² + HF² = AH²
∆ABC vuông tại A vó AH là đường cao
⇒ AH² = HB.HC
⇒ AE.EB + AF.FC = HB.HC
⇒ AE.EB + AF.FC - HB.HC = 0
c) AH = EF đã chứng minh ở câu b
Đúng 2
Bình luận (0)
giúp bài 1 và bài 2 với ạ mình cảm ơn
cho tam giác abc vuông tại a đường cao AI. biết AC=15cm , AI= 12cm.
a)Tính CI, IB,BC,AB
b) Kẻ IK vuông góc AB, IE vuông góc AC. Tính KE
GIÚP MIK VS
a: ΔACI vuông tại I
=>\(IA^2+IC^2=AC^2\)
=>\(IC^2=15^2-12^2=81\)
=>IC=9(cm)
Xét ΔCAB vuông tại A có AI là đường cao
nên \(CA^2=CI\cdot CB\)
=>CB=15^2/9=25(cm)
CI+IB=CB
=>IB+9=25
=>IB=16cm
ΔIAB vuông tại I
=>\(IA^2+IB^2=AB^2\)
=>\(AB^2=12^2+16^2=400\)
=>AB=20(cm)
b: Xét tứ giác AKIE có
\(\widehat{AKI}=\widehat{AEI}=\widehat{KAE}=90^0\)
Do đó: AKIE là hình chữ nhật
=>AI=KE
=>KE=12(cm)
Đúng 0
Bình luận (0)
 \(giúp em câu 1,2 với ạ\)
\(giúp em câu 1,2 với ạ\)
1.
Do $a>1$ nên $a-1>0; 2a+1>0$. Khi đó
$A=\sqrt{(a-1)^2(2a+1)^2}=\sqrt{(a-1)^2}.\sqrt{(2a+1)^2}$
$=|a-1|.|2a+1|=(a-1)(2a+1)$
2.
$B=\sqrt{(b-1)(b+7)+16}=\sqrt{b^2+6b-7+16}=\sqrt{b^2+6b+9}$
$=\sqrt{(b+3)^2}=|b+3|=-(b+3)$ do $b+3<0$ với mọi $b< -3$
Đúng 0
Bình luận (0)