Trục căn thức ở mẫu của các biểu thức sau :
4/ căn 3 ;2/ căn 5-1
Trục căn thức ở mẫu của các biểu thức sau:
\(\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}\); \(\dfrac{1}{\sqrt{3}+\sqrt{2}+1}\)
\(\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}=\dfrac{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{2}.\sqrt{2}}=\dfrac{\sqrt{10}-\sqrt{6}}{2}\)
\(\dfrac{1}{\sqrt{3}+\sqrt{2}+1}=\dfrac{\sqrt{3}-\sqrt{2}-1}{\left(\sqrt{3}+\sqrt{2}+1\right)\left(\sqrt{3}-\sqrt{2}-1\right)}\)
\(=\dfrac{\sqrt{3}-\sqrt{2}-1}{3-\left(\sqrt{2}+1\right)^2}=\dfrac{\sqrt{3}-\sqrt{2}-1}{-2\sqrt{2}}=\dfrac{\left(\sqrt{3}-\sqrt{2}-1\right)\sqrt{2}}{-2\sqrt{2}.\sqrt{2}}=\dfrac{\sqrt{6}-2-\sqrt{2}}{-4}\)
\(=\dfrac{2+\sqrt{2}-\sqrt{6}}{4}\)
\(\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}=\dfrac{\sqrt{10}-\sqrt{6}}{2}\)
\(\dfrac{1}{\sqrt{3}+\sqrt{2}+1}=\dfrac{2+\sqrt{2}-\sqrt{6}}{4}\)
\(\dfrac{1}{1+\sqrt[3]{2}+2\sqrt[3]{4}}\)Trục căn thức ở mẫu của biểu thức sau:
Trục căn thức ở mẫu của biểu thức
a) \(\dfrac{4}{3-5}\)
b) \(\dfrac{2}{5+\sqrt{7}}\)
Trục căn thức ở mẫu của biểu thức sau :
1 phần 1 cộng căn bậc hai cộng căn bậc ba (sr mik ko bt viết)
Trục căn thức ở mẫu biểu thức \(\dfrac{5}{3\sqrt{8}}\)
\(\dfrac{5}{3\sqrt{8}}=\dfrac{5}{6\sqrt{2}}=\dfrac{5.\sqrt{2}}{6.2}=\dfrac{5\sqrt{2}}{12}\)
\(\dfrac{5}{3\sqrt{8}}=\dfrac{5\sqrt{2}}{12}\)
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
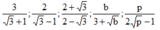
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa
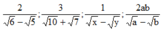
1) thực hiện phép tính
\(3\sqrt{12}+\dfrac{1}{2}\sqrt{48}-\sqrt{27}\)
2) trục căn thức ở mẫu : \(\dfrac{2}{\sqrt{3}-5}\)
3) khử mẫu của biểu thức lấy căn: \(\sqrt{\dfrac{2}{5}}\)
1) Ta có: \(3\sqrt{12}+\dfrac{1}{2}\sqrt{48}-\sqrt{27}\)
\(=3\cdot2\sqrt{3}+\dfrac{1}{2}\cdot4\sqrt{3}-3\sqrt{3}\)
\(=6\sqrt{3}+2\sqrt{3}-3\sqrt{3}\)
\(=5\sqrt{3}\)
2) Ta có: \(\dfrac{2}{\sqrt{3}-5}\)
\(=\dfrac{2\left(\sqrt{3}+5\right)}{\left(\sqrt{3}-5\right)\left(\sqrt{3}+5\right)}\)
\(=\dfrac{2\left(\sqrt{3}+5\right)}{3-25}\)
\(=\dfrac{-2\left(\sqrt{3}+5\right)}{22}\)
\(=\dfrac{-\sqrt{3}-5}{11}\)
3) Ta có: \(\sqrt{\dfrac{2}{5}}\)
\(=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(=\dfrac{\sqrt{2}\cdot\sqrt{5}}{5}\)
\(=\dfrac{\sqrt{10}}{5}\)
Trục căn thức ở mẫu của biểu thức : \(\dfrac{1}{\sqrt{a}-1}\)
\(\dfrac{1}{\sqrt{a}-1}\)
\(=\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{\sqrt{a}+1}{\left(\sqrt{a}\right)^2-1^2}\)
\(=\dfrac{\sqrt{a}+1}{a-1}\)