Giải phương trình:
\(\sqrt{3x+1}-\sqrt{6-x}+3x^2-14x-8=0\)
Giải phương trình:
\(\sqrt{3x+1}-\sqrt{6-x}+3x^2-14x-8=0\)
ĐKXĐ: \(-\dfrac{1}{3}\le x\le6\)
\(\left(\sqrt{3x+1}-4\right)+\left(1-\sqrt{6-x}\right)+\left(3x^2-14x-5\right)=0\)
\(\Leftrightarrow\dfrac{3\left(x-5\right)}{\sqrt{3x+1}+4}+\dfrac{x-5}{1+\sqrt{6-x}}+\left(x-5\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(\dfrac{3}{\sqrt{3x+1}+4}+\dfrac{1}{1+\sqrt{6-x}}+3x+1\right)=0\)
\(\Leftrightarrow x-5=0\) (do \(\dfrac{3}{\sqrt{3x+1}+4}+\dfrac{1}{1+\sqrt{6-x}}+3x+1>0;\forall x\))
\(\Rightarrow x=5\)
ĐKXĐ: \(\left\{{}\begin{matrix}3x+1>=0\\6-x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{1}{3}\\x< =6\end{matrix}\right.\)
\(\sqrt{3x+1}-\sqrt{6-x}+3x^2-14x-8=0\)
=>\(\sqrt{3x+1}-4+1-\sqrt{6-x}+3x^2-14x-5=0\)
=>\(\dfrac{3x+1-16}{\sqrt{3x+1}+4}+\dfrac{1-6+x}{1+\sqrt{6-x}}+3x^2-15x+x-5=0\)
=>\(\dfrac{3\cdot\left(x-5\right)}{\sqrt{3x+1}+4}+\dfrac{x-5}{\sqrt{6-x}+1}+\left(x-5\right)\left(3x+1\right)=0\)
=>\(\left(x-5\right)\left(\dfrac{3}{\sqrt{3x+1}+4}+\dfrac{1}{\sqrt{6-x}+1}+3x+1\right)=0\)
=>x-5=0
=>x=5(nhận)
a: ĐKXĐ: \(x\notin\left\{0;-1\right\}\)
\(P=\left(\dfrac{1}{x}+\dfrac{x}{x+1}\right):\dfrac{x}{x^2+x}\)
\(=\dfrac{x+1+x^2}{x\left(x+1\right)}\cdot\dfrac{x^2+x}{x}\)
\(=\dfrac{x^2+x+1}{x}\)
b: \(P=\dfrac{x^2+x+1}{x}\)
\(=x+1+\dfrac{1}{x}\)
Ta có: \(x+\dfrac{1}{x}>=2\cdot\sqrt{x\cdot\dfrac{1}{x}}=2\forall x>0\)
=>\(P=x+\dfrac{1}{x}+1>=2\cdot\sqrt{x\cdot\dfrac{1}{x}}+2=3\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x^2=1\\x>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{1;-1\right\}\\x>0\end{matrix}\right.\)
=>x=1
Bài 1: a, Tìm GTNN của A = ∣x - 3∣ + ∣x - 4∣ + ∣x - 7∣ b, Tìm x, y thoả mãn ∣x - 2∣ + ∣ y²⁰ + 9∣ = 9
a.
\(A=\left|x-3\right|+\left|x-4\right|+\left|x-7\right|\)
\(A=\left|x-3\right|+\left|7-x\right|+\left|x-4\right|\)
Áp dụng BĐT trị tuyệt đối:
\(A\ge\left|x-3+7-x\right|+\left|x-4\right|\)
\(\Rightarrow A\ge4+\left|x-4\right|\ge4\)
\(\Rightarrow A_{min}=4\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\left(x-3\right)\left(7-x\right)\ge0\\x-4=0\end{matrix}\right.\) \(\Rightarrow x=4\)
Câu b đã giải bên dưới
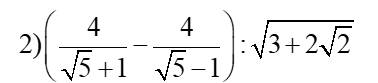
GIÚP MÌNH VSSS, MÌNH ĐANG CẦN GẤP Ạ
\(\left(\dfrac{4}{\sqrt{5}+1}-\dfrac{4}{\sqrt{5}-1}\right):\sqrt{3+2\sqrt{2}}\)
\(=\left(\dfrac{4\left(\sqrt{5}-1\right)-4\left(\sqrt{5}+1\right)}{4}\right):\left(\sqrt{2}+1\right)\)
\(=\dfrac{\left(\sqrt{5}-1-\sqrt{5}-1\right)}{\sqrt{2}+1}=\dfrac{-2}{\sqrt{2}+1}=-2\left(\sqrt{2}-1\right)=-2\sqrt{2}+2\)
tìm x
2 \(\sqrt{16x-16}\)+\(\sqrt{49x-49}\) \(-\) \(\sqrt{x-1}\) =46
ĐKXĐ: x>=1
\(PT\Leftrightarrow8\sqrt{x-1}+7\sqrt{x-1}-\sqrt{x-1}=46\)
=>\(14\sqrt{x-1}=46\)
=>\(\sqrt{x-1}=\dfrac{23}{7}\)
=>\(x-1=\dfrac{529}{49}\)
=>\(x=\dfrac{578}{49}\)
2\(\sqrt{1\text{6}x-1\text{6}}\)+\(\sqrt{49x-49}\)-\(\sqrt{x-1}\)=46
<=>2.4.4\(\sqrt{x-1}\)+7.7\(\sqrt{x-1}\)-\(\sqrt{x-1}\)=46
<=> 32\(\sqrt{x-1}\)+49\(\sqrt{x-1}\)-\(\sqrt{x-1}\)=46
<=> (32+49-1)\(\sqrt{x-1}\)=46
<=> 80\(\sqrt{x-1}\)=46
<=> \(\sqrt{x-1}\)=\(\dfrac{23}{40}\)
<=> x-1=\(\dfrac{529}{1\text{6}00}\)
<=> x=\(\dfrac{2159}{1\text{6}00}\)
<=>x=1,35
tìm x
2\(\sqrt{16x-16}\) +\(\sqrt{41-4y}\) -\(\sqrt{x-1}\) =46
các bạn giúp mik vs ạ

bài 4 nhá
Câu 4:
1: Gọi AB là chiều cao của tháp; D,C lần lượt là điểm mà anh trên tháp thấy xe máy đang chạy.
Theo đề, ta có: AB=100m; AB\(\perp\)DB tại B; \(\widehat{ADB}=30^0;\widehat{ACB}=60^0\)
Xét ΔABD vuông tại B có \(sinD=\dfrac{AB}{AD}\)
=>\(\dfrac{100}{AD}=sin30=\dfrac{1}{2}\)
=>\(AD=200\left(m\right)\)
Ta có: ΔABD vuông tại B
=>\(BA^2+BD^2=AD^2\)
=>\(BD^2=200^2-100^2=30000\)
=>\(BD=100\sqrt{3}\left(m\right)\)
Ta có: \(\widehat{ACB}+\widehat{ACD}=180^0\)(hai góc kề bù)
=>\(\widehat{ACD}=180^0-60^0=120^0\)
Xét ΔCAD có \(\widehat{D}+\widehat{ACD}+\widehat{CAD}=180^0\)
=>\(\widehat{CAD}+120^0+30^0=180^0\)
=>\(\widehat{CAD}=30^0\)
Xét ΔCAD có \(\dfrac{AD}{sinACD}=\dfrac{DC}{sinDAC}\)
=>\(\dfrac{200}{sin120}=\dfrac{DC}{sin30}\)
=>\(DC=\dfrac{200\sqrt{3}}{3}\left(m\right)\)
=>Sau 6 phút thì xe máy đi được quãng đường là \(\dfrac{200\sqrt{3}}{3}\left(m\right)\)
Vận tốc của xe máy là: \(\dfrac{200\sqrt{3}}{3}:6=\dfrac{200\sqrt{3}}{18}=\dfrac{100\sqrt{3}}{9}\left(\dfrac{m}{p}\right)\)
Thời gian xe máy đến chân tháp là:
\(100\sqrt{3}:\dfrac{100\sqrt{3}}{9}=9\left(phút\right)\)
2:
a: ΔDAC vuông tại D
=>\(AC^2=DA^2+DC^2\)
=>\(AC^2=6^2+8^2=100\)
=>\(AC=\sqrt{100}=10\left(cm\right)\)
Xét ΔDAC vuông tại D có DH là đường cao
nên \(DH\cdot AC=DA\cdot DC\)
=>\(DH\cdot10=6\cdot8=48\)
=>DH=48/10=4,8(cm)
Xét ΔADC vuông tại D có \(sinACD=\dfrac{AD}{AC}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{ACD}\simeq36^052'\)
b: Xét ΔDAC vuông tại D có DH là đường cao
nên \(AH\cdot AC=AD^2;CH\cdot CA=CD^2\)
=>\(\dfrac{AH\cdot AC}{CH\cdot AC}=\dfrac{AD^2}{CD^2}\)
=>\(\dfrac{AH}{CH}=\dfrac{BC^2}{AB^2}=\left(\dfrac{BC}{AB}\right)^2\)
c: Gọi K là trung điểm của DH
Xét ΔHAD có
F,K lần lượt là trung điểm của HA,HD
=>FK là đường trung bình của ΔHAD
=>FK//AD và \(FK=\dfrac{AD}{2}\)
ta có: FK//AD
AD\(\perp\)DC
Do đó: FK\(\perp\)DC
Xét ΔFDC có
FK,DH là các đường cao
FK cắt DH tại K
Do đó: K là trực tâm của ΔFDC
=>FK\(\perp\)DC
Ta có: FK//AD
BC//AD
Do đó: FK//BC
Ta có: \(FK=\dfrac{AD}{2}\)
\(CE=\dfrac{CB}{2}\)
mà AD=CB
nên FK=CE
Xét tứ giác FKCE có
FK//CE
FK=CE
Do đó: FKCE là hình bình hành
=>CK//FE
Ta có: CK//FE
CK\(\perp\)FD
Do đó: FE\(\perp\)FD
\(\sqrt{x+2}+\sqrt{9x+18}=\sqrt{4x+8+6}\)
\(\sqrt{x+2}+\sqrt{9x+18}=\sqrt{4x+8+6}\)
\(\sqrt{x+2}+\sqrt{9\left(x+2\right)}=\sqrt{4x+14}\) \(\left(Đk:x\ge-2\right)\)
\(4\sqrt{x+2}=\sqrt{4x+14}\)
\(16\left(x+2\right)=4x+14\)
\(12x=-18\)
\(x=-\dfrac{3}{2}\left(TM\right)\)
Vậy \(S=\left\{-\dfrac{3}{2}\right\}\)
\(\sqrt{1-3x}=4\)
\(\Leftrightarrow1-3x=4\)
\(\Leftrightarrow3x=-3\)
\(\Leftrightarrow x=-1\)
c)
\(=5\sqrt{3x}-4.\sqrt{4.3x}+5\sqrt{9.3x}+26\\ =5\sqrt{3x}-8\sqrt{3x}+15\sqrt{3x}+26\\= \left(5-8+15\right)\sqrt{3x}+26\\ =12\sqrt{3x}+26\)
d)
\(\dfrac{1}{xy}\sqrt{x^4y^3}\\ =\dfrac{1}{xy}\sqrt{\left(x^2\right)^2.y^2.y}\\ =\dfrac{1}{xy}x^2.y.\sqrt{y}\\ =\dfrac{x.y.x.\sqrt{y}}{xy}\\ =x\sqrt{y}\)
e)
\(8\sqrt{x^3y^2}-3y\sqrt{x^3}\\ =8\sqrt{x^2.x.y^2}-3y\sqrt{x^2.x}\\ =8xy\sqrt{x}-3xy\sqrt{x}\\ =\left(8xy-3xy\right)\sqrt{x}\\ =5xy\sqrt{x}\)