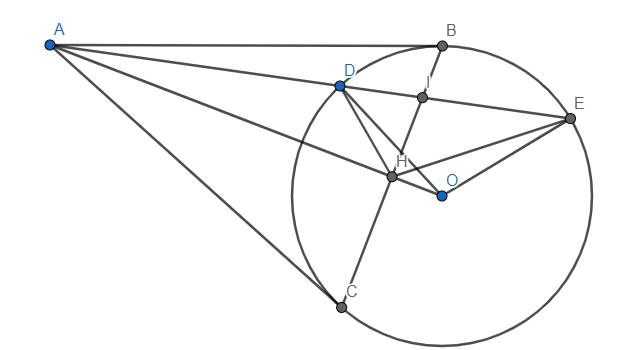
Qua điểm A kẻ hai tiếp tuyến AB,AC của (O ;r) ( B,C là tiếp điểm ) M là điểm bất kì trên cung nhỏ BC ,vẽ tiếp tuyến của đường tròn tại M cắt hai tiếp tuyến AB,AC tại I và K, tìm vị trí của M để
a)IK có độ dài nhỏ nhất
b) S(AIK) có giá trị lớn nhất
c) Đường cao AH của tgAIK có giá trị lớn nhất
Giúp mình với cảm ơn mọi người nhiều!