Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm A và B. Vẽ đường kính AC và AD của đường tròn (O) và (O'). Tia AC cắt (O') tại F, tia DA cắt (O) tại E.
b, CM tứ giác EOO'F nội tiếp
Ôn tập góc với đường tròn
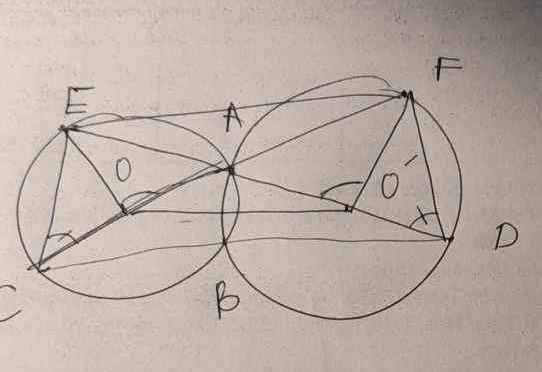
Ta thấy góc EAO = góc FAO' (đối đỉnh) (1)
Lại có OE = OA (vì đều là bán kính của đường tròn (O)) → ΔOEA cân tại O
→ Góc EAO = góc AEO (2)
Từ (1) và (2) → Góc FAO' = góc AEO (cùng bằng góc EAO)
Suy ra tứ giác EOO'F nội tiếp (2 góc kề nhau cùng nhìn 1 đường thẳng)
Đúng 1
Bình luận (0)
Giúp mình bài này với ạ ( câu b, câu c )

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó:H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
Xét tứ giác BEHF có \(\widehat{BEH}+\widehat{BFH}=90^0+90^0=180^0\)
nên BEHF là tứ giác nội tiếp
b: Ta có: \(\widehat{BED}+\widehat{BCD}=180^0\)(B,E,D,C cùng thuộc (O))
\(\widehat{BED}+\widehat{SEB}=180^0\)(hai góc kề bù)
Do đó: \(\widehat{SEB}=\widehat{SCD}\)
Xét ΔSEB và ΔSCD có
\(\widehat{SEB}=\widehat{SCD}\)
\(\widehat{ESB}\) chung
Do đó: ΔSEB~ΔSCD
=>\(\dfrac{SE}{SC}=\dfrac{SB}{SD}\)
=>\(SE\cdot SD=SB\cdot SC\)
Đúng 0
Bình luận (0)
Giúp mình với ạ.
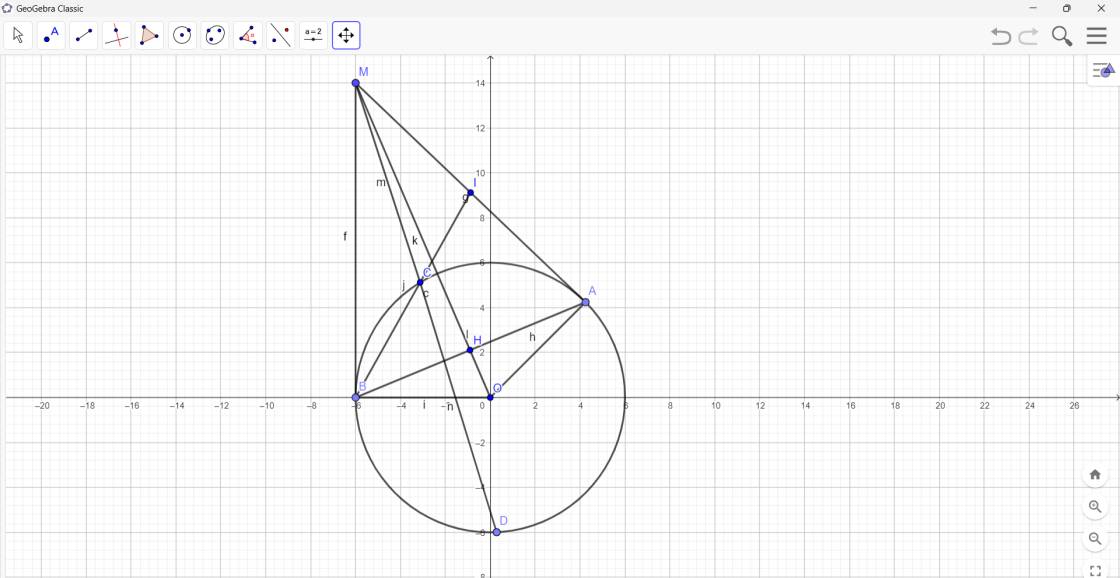
Cho tam giác ABC nhọn (AB < AC ) nội tiếp đường tròn (O), có đường cao AD, AD cắt (O) tại điểm thứ hai là M. Vẽ ME vuông góc với AC (E thuộc AC), đường thẳng ED cắt đường thẳng AB tại I.
a) Tính AIM và chứng minh AB.AI=AD.AM.
c) Gọi N là điểm đối xứng với M qua l, F là điểm đối xứng với M qua E. NF cắt AD tại H. Chứng minh BH // MF
Mọi người giúp mình bài 5 với. Mình cảm ơn

a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{MBC}\) là góc tạo bởi tiếp tuyến BM và dây cung BC
\(\widehat{BDC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{MBC}=\widehat{BDC}\)
Xét ΔMBC và ΔMDB có
\(\widehat{MBC}=\widehat{MDB}\)
\(\widehat{BMC}\) chung
Do đó: ΔMBC~ΔMDB
=>\(\dfrac{MB}{MD}=\dfrac{MC}{MB}\)
=>\(MB^2=MD\cdot MC\)
Đúng 1
Bình luận (0)
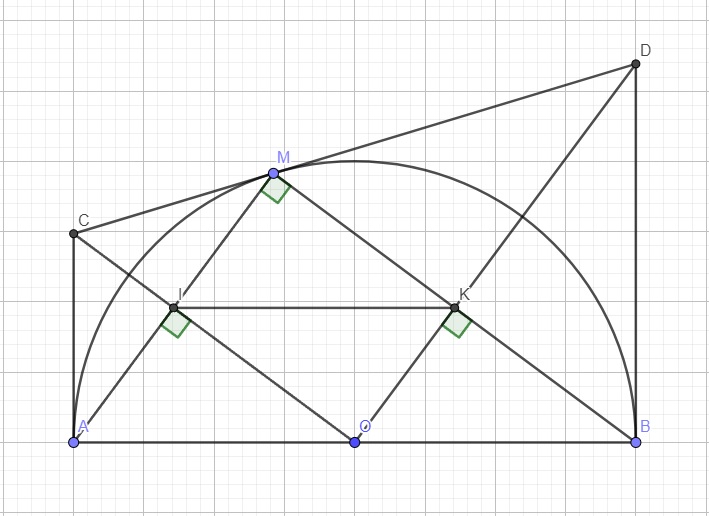
cho nửa đường tròn (O) đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By với nửa đường tròn. M là một điểm trên nửa đường tròn. Tiếp tuyến với nửa đường tròn tại M cắt Ax, By tương ứng tại C và D. Nối OC cắt AM tại I, nối OD cắt Bm tại K. Cm: CIKD là tứ giác nt
Do C là giao 2 tiếp tuyến tại M và A nên \(CM=CA\)
Lại có \(OM=OA=R\)
\(\Rightarrow OC\) là trung trực của AM
\(\Rightarrow I\) là trung điểm AM và \(OC\perp AM\) tại I
Tương tự, ta có OD là trung trực BM nên K là trung điểm BM và \(OD\perp BM\) tại K
\(\Rightarrow\) IK là đường trung bình tam giác MAB
\(\Rightarrow IK||AB\Rightarrow\widehat{MIK}=\widehat{MAB}\) (đồng vị)
Mà \(\widehat{MAB}+\widehat{MBA}=90^0\) (do \(\widehat{AMB}=90^0\) góc nt chắn nửa đường tròn)
\(\Rightarrow\widehat{MIK}+\widehat{MBA}=90^0\) (1)
DB là tiếp tuyến tại B \(\Rightarrow\widehat{DBO}=90^0\Rightarrow\widehat{ODB}=\widehat{MAB}\) (cùng phụ \(\widehat{OKB}\)) (2)
Theo t/c hai tiếp tuyến cắt nhau, \(\widehat{ODB}=\widehat{ODC}\) (3)
\(\left(1\right);\left(2\right);\left(3\right)\Rightarrow\widehat{MIK}+\widehat{ODC}=90^0\)
\(\Rightarrow\widehat{CIK}+\widehat{ODC}=\widehat{CIM}+\widehat{MIK}+\widehat{ODC}=90^0+90^0=180^0\)
\(\Rightarrow CIKD\) nội tiếp
Đúng 3
Bình luận (0)
Cho(O;R) và A nằm bên ngoài đường tròn, vẽ tiếp tuyến AB( B là tiếp điểm) vẽ dây BC của đường tròn sau cho BC vuông góc vs OA tại H. Trên tia đối của tia BC lấy điểm Q. Từ Q vẽ 2 tiếp tuyến QD, QE đến đươbgf tròn (D,E là tiếp điểm) a) Cm: QDOE là tứ giác nội tiếp b) Cm: A,D,E thẳng hàng
a: Xét tứ giác QDOE có \(\widehat{QDO}+\widehat{QEO}=90^0+90^0=180^0\)
nên QDOE là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A(O;AB) cắt BC tại D. Kẻ OH vuông góc với BD. Đường cao AK của tam giác ACO cắt OH tại M a) Chứng minh OH.OM= OK.OC b) Chứng minh MD là tiếp tuyến của đường tròn Giải giúp mình với
a: Xét ΔOKM vuông tại K và ΔOHC vuông tại H có
\(\widehat{KOM}\) chung
Do đó: ΔOKM~ΔOHC
=>\(\dfrac{OK}{OH}=\dfrac{OM}{OC}\)
=>\(OK\cdot OC=OH\cdot OM\)
b: Xét ΔACO vuông tại A có AK là đường cao
nên \(OK\cdot OC=OA^2=R^2\)
=>\(OD^2=OH\cdot OM\)
=>\(\dfrac{OD}{OH}=\dfrac{OM}{OD}\)
Xét ΔODM và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OM}{OD}\)
\(\widehat{DOM}\) chung
Do đó: ΔODM~ΔOHD
=>\(\widehat{ODM}=\widehat{OHD}=90^0\)
=>MD là tiếp tuyến của (O)
Đúng 1
Bình luận (0)
Giúp mình câu c,e,f với ạ
c: Ta có: \(MH\cdot MO=ME\cdot MF\)
=>\(\dfrac{MH}{MF}=\dfrac{ME}{MO}\)
Xét ΔMHE và ΔMFO có
\(\dfrac{MH}{MF}=\dfrac{ME}{MO}\)
\(\widehat{HME}\) chung
Do đó: ΔMHE~ΔMFO
=>\(\widehat{MHE}=\widehat{MFO}\)
mà \(\widehat{MHE}+\widehat{OHE}=180^0\)
nên \(\widehat{OHE}+\widehat{OFE}=180^0\)
=>OHEF là tứ giác nội tiếp
Đúng 1
Bình luận (0)
Cho tam giác ABC (ABAC) có 3 góc nhọn nội tiếp (O).Các đường cao BD,CE,AF của tam giác ABC cắt nhau tại H.a) CM:BCDE nội tiếp và tam giác ADE đồng dạng với tam giác ABC.b) Vẽ đường kính AK của (O). Gọi giao điểm của AK và DE là I. CM: AK vuông góc với DE và DE.CFEI.BC.c) Tiếp tuyến B của (O) cắt DE tại N và giao điểm của HK và BC là M.CM: CE song song với MN.(MÌNH CẦN GẤP!!!)
Đọc tiếp
Cho tam giác ABC (AB<AC) có 3 góc nhọn nội tiếp (O).Các đường cao BD,CE,AF của tam giác ABC cắt nhau tại H.
a) CM:BCDE nội tiếp và tam giác ADE đồng dạng với tam giác ABC.
b) Vẽ đường kính AK của (O). Gọi giao điểm của AK và DE là I. CM: AK vuông góc với DE và DE.CF=EI.BC.
c) Tiếp tuyến B của (O) cắt DE tại N và giao điểm của HK và BC là M.CM: CE song song với MN.
(MÌNH CẦN GẤP!!!)
a: Xét tứ giác BCDE có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BCDE là tứ giác nội tiếp
=>\(\widehat{BED}+\widehat{BCD}=180^0\)
mà \(\widehat{BED}+\widehat{AED}=180^0\)(hai góc kề bù)
nên \(\widehat{AED}=\widehat{ACB}\)
Xét ΔAED và ΔACB có
\(\widehat{AED}=\widehat{ACB}\)
\(\widehat{EAD}\) chung
Do đó: ΔAED~ΔACB
b: Gọi Ax là tiếp tuyến tại A của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{ADE}\)(ΔABC~ΔADE)
nên \(\widehat{xAC}=\widehat{ADE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//DE
=>AK\(\perp\)DE
Đúng 2
Bình luận (0)
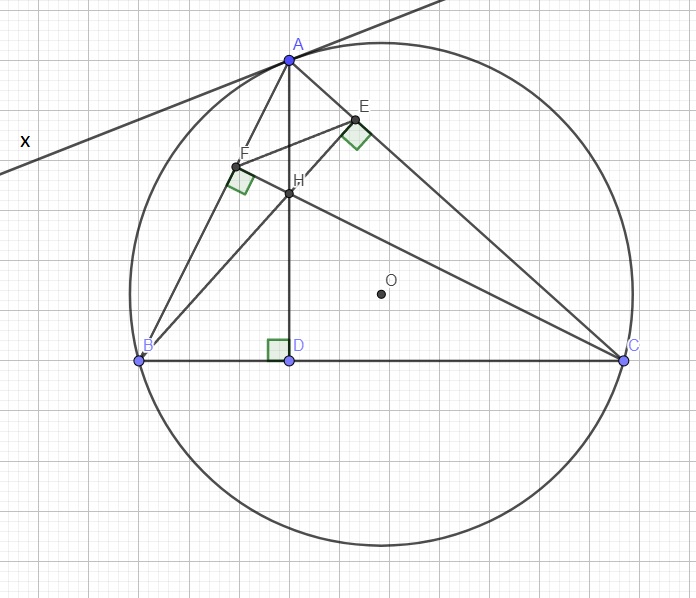
Cho tam giác ABC nhọn nội tiếp (O),các đường cao AD,BE,CF cắt nhau tại H.Chứng minh
a)Tứ giác BFEC nội tiếp
b)AE.AC=AF.AB
c)H là tâm đường tròn nội tiếp tam giác DEF
d)OA vuông góc EF
giup minh voi
c.
Theo giả thiết E và F cùng nhìn AH dưới 1 góc vuông
\(\Rightarrow AEHF\) nội tiếp
\(\Rightarrow\widehat{HEF}=\widehat{HAF}\) (cùng chắn HF)
E và D cùng nhìn AB dưới 1 góc vuông
\(\Rightarrow ABDE\) nội tiếp
\(\Rightarrow\widehat{BED}=\widehat{BAD}\) (cùng chắn BD) hay \(\widehat{BED}=\widehat{HAF}\)
\(\Rightarrow\widehat{HEF}=\widehat{BED}\)
\(\Rightarrow EH\) là phân giác của \(\widehat{DEF}\)
Chứng minh hoàn toàn tương tự ta có FH là phân giác của \(\widehat{DFE}\)
\(\Rightarrow H\) là giao điểm 2 đường phân giác trong của tam giác DEF
\(\Rightarrow H\) là tâm đường tròn nội tiếp tam giác DEF
d.
Trong đường tròn (O), qua A kẻ tiếp tuyến Ax
\(\Rightarrow Ax\perp OA\) (1)
Ta có: \(\widehat{BAx}=\widehat{BCA}\) (cùng chắn AB)
Mà \(\widehat{BCA}=\widehat{AFE}\) (theo cm câu b)
\(\Rightarrow\widehat{BAx}=\widehat{AFE}\)
\(\Rightarrow Ax||EF\) (hai góc so le trong bằng nhau) (2)
(1);(2) \(\Rightarrow OA\perp EF\)
Đúng 1
Bình luận (0)
a.
\(\left\{{}\begin{matrix}BE\perp CE\left(gt\right)\\BF\perp CF\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\) \(\widehat{BEC}=\widehat{BFC}=90^0\)
\(\Rightarrow\) Hai điểm E và F cùng nhìn BC dưới 1 góc vuông nên tứ giác BFEC nội tiếp
b.
Do BFEC nội tiếp \(\Rightarrow\widehat{BFE}+\widehat{BCA}=180^0\)
Mà \(\widehat{AFE}+\widehat{BFE}=180^0\) (hai góc kề bù)
\(\Rightarrow\widehat{AFE}=\widehat{BCA}\)
Xét hai tam giác ABC và AEF có:
\(\left\{{}\begin{matrix}\widehat{A}-chung\\\widehat{BCA}=\widehat{AFE}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABC\sim\Delta AEF\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AE}=\dfrac{AC}{AF}\Rightarrow AE.AC=AF.AB\)
Đúng 1
Bình luận (0)