cho đường trìn (O) bán kính OA=R ; đường trung trực của OA cắt (O) lâbf lượt tại C và D kể tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng A tại M
a) tứ giác OCAD là hình gì
b) tính CM theo R
c) chứng minh MD là tiếp tuyến của (O)
cho đường tròn tâm o bán kính r và điểm a nằm ngoài đường tròn. đường tròn đường kính oa cắt đường tròn tâm o bán kính r tại m và n, đường thẳng đi qua a cắt đường tròn tâm o bán kính r tại b và c. b thuộc đoạn ac. gọi h là trung điểm của bc.
a) am là tiếp tuyến của đường tròn tâm o bán kính r.
b) Đường thẳng qua B vuông góc với OM cắt MN tại d. chứng minh
1) góc AHN = góc BDN
2) DH // MC
Cho một điểm M thuộc đường tròn tâm O đường kính R. Vẽ đường tròn tâm O' bán kính r có đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
a) Chứng minh cung MA và cung MB có độ dài bằng nhau.
b) Biết góc AOM = 450 và R = 10cm. Tính diện tích giới hạn bởi cung MA, cung MB và đoạn AB.
Cho một điểm M thuộc đường tròn tâm O đường kính R. Vẽ đường tròn tâm O' bán kính r có đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
a) Chứng minh cung MA và cung MB có độ dài bằng nhau.
b) Biết góc AOM = 45 độ và R = 10cm. Tính diện tích giới hạn bởi cung MA, cung MB và đoạn AB.
Cho tam giác OAB cân có OA=OB=5cm và AB=6cm . Hỏi bán kính r của đường tròn tâm O bán kính r bằng bao nhiêu để đường tròn tiếp xúc AB
Mình chỉ nêu cách giải thôi nha, ko có biết trình bày đâu à
Câu 1 (bạn tự vẽ hình và xem câu trả lời của mình có ổn không nhé)
a. - ta có góc A = 90.
- Xét tam giác BEH, áp dụng định lí tam giác có đường trung tuyến ứng vs cạnh huyền bằng nửa cạnh huyền là tam giác vuông (IE = IB = IH = R đường tròn tâm I = BH/2). Ta có góc BEH bằng 90, suy ra góc AEH bằng 90 vì kề bù.
- Chứng minh tương tự với tam giác CHF, ta có góc F bằng 90.
=> Xét tứ giác AEHF ta có A = E = F = 90 theo cmt, nên AEHF là hình chữ nhật.
- vì AEHF là hình chữ nhật nên AH = EF. Áp dụng hệ thức lượng tính ra AH = căn của AB.AC = căn 48 = 4 căn 3.
b, Xét hình chữ nhật AEHF, gọi giao điểm của hai đường chéo là O. Áp dụng các tính chất của hình chữ nhật (hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường), cm được OA = OE = OF = OH. O là tâm, bán kính là OA = OE = OF = OH.
c. Trước hết, KF giao EF tại F.
*. Cm góc OFK bằng 90.
- KH = KF = bán kính đường tròn tâm K. Suy ra KHF cân tại K, góc KHF = KFH.
- OF = OH theo cm ở câu b, nên OHF = OFH.
Nên KFH + OFH = KHF + OHF = 90.
Mà KFH + OFH = OFK. => OFK = 90.
Kết luận : KF là tiếp tuyến.
Câu 2
- Lấy I là trung điểm OA.
Xét tam giác vuông OBA (góc B = 90 vì AB là tiếp tuyến), ta có IO = IA ( I là trung điểm) = IB (định lí). Cm tương tự, IO = IA = IC.
=> I là tâm đường tròn cần tìm, bán kính là IA/2.
- Áp dụng định lí Pytago, tìm được OB.
Câu 3
Để hai đồ thị vuông góc với nhau thì a.a' = -1
=> a = -1.
Để đồ thị đã cho đi qua M thì toạ độ của M thoả mãn phương trình đồ thị đó.
Thay x = -1, y =4 vào phương trình đã cho, ta có
y = ax + b <=> -1.-1 + b = 4 <=> b = 3.
Vậy a = -1, b = 3.
Câu 4
đồ thị đã cho sẽ đi qua 2 điểm là (0 ; b) = (0 ; -2m) và (-b/a ; 0) = (2 ; 0)
Suy ra đồ thị giao với trục hoành tại điểm 2 => OA = 2.
Để tam giác có diện tích là 2, đoạn OB phải có độ dài là
OA.OB : 2 = 2
=> OB = 4 : 2 = 2. bạn tính tiếp nha vì câu này thì mình ko chắc kết quả đúng ko nữa, mình dốt hàm số tệ
Câu 5
a, Áp dụng hệ thức lượng số 2 trong sgk, tính ra AH = căn 30.
Áp dụng định lí Pytago, tính được BC = căn 61
Áp dụng hệ thực lượng số 1 trong sgk, tính được BH = 25 : căn 61 và CH = 36 : căn 61.
Tâm đường tròn ngoại tiếp tam giác ABC là giao điểm 3 đường trung trực là trung điểm cạnh huyền (tam giác ABC vuông), suy ra bán kính đường tròn ngoại tiếp là căn 61 : 2.
b, Cm tứ giác là hình chữ nhật thì làm giống câu 1, phần a.
Đặt các điểm I, K tương tự như câu 1, cm vuông góc cũng giống câu 1 ấy mà.
Cho đường tròn tâm O bán kính R, có hai đường kính AB và CD vuông góc với nhau.
Trên bán kính OA lấy điểm I sao cho AI=2/3 R
. Tia CI cắt đường tròn (O) tại điểm thứ hai E.
a) Chứng minh tam giác COI và tam giác CED đồng dạng
b) Tính độ dài dây CE.
b.
Áp dụng định lý Pitago trong tam giác vuông COI:
\(CI=\sqrt{OC^2+OI^2}=\sqrt{R^2+\left(\dfrac{R}{3}\right)^2}=\dfrac{R\sqrt{10}}{3}\)
Do 2 tam giác COI và CED đồng dạng
\(\Rightarrow\dfrac{CE}{CO}=\dfrac{CD}{CI}\Rightarrow CE=\dfrac{CD.CO}{CI}=\dfrac{2R.R}{\dfrac{R\sqrt{10}}{3}}=\dfrac{3R\sqrt{10}}{5}\)
a: Xét (O) có
ΔCED nội tiếp đường tròn
CD là đường kính
Do đó: ΔCED vuông tại E
Xét ΔCOI vuông tại O và ΔCED vuông tại E có
\(\widehat{ICO}\) chung
Do đó: ΔCOI\(\sim\)ΔCED
Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.
Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.
Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => ΔAOB đều => ∠AOB = 60o
Trong tam giác OBE vuông tại B ta có:
BE = OB.tg∠AOB = OB.tg60o = R.√3
cho đường tròn tâm o bán kính R= 3 và A là điểm nằm ngoài đường tròn sao cho OA = 5 . Kẻ tiếp tuyến AB,AC với đường tròn tâm O. cm OA vuôn góc BC
Cho đường tròn tâm O bán kính R, dây BC khác đường kính, Hai tiếp tuyến của đường tròn (O;R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a) Chứng minh $AO \bot BC.$
b) Cho biết $R = 15, BC = 24 (cm).$ Tính AB, OA.
c) Chứng minh BC là tia phân giác $\widehat{ABH}.$
Em cần câu c thôi ạ.
Hình vẽ.
\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)
Cho đường tròn (O), bán kính OA, dây CD là đường trung trực của OA. Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Tính độ dài CI biết OA = R.
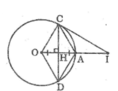
Vì ACOD là hình thoi nên AC = OC
Mà OC = OA (= R) nên tam giác OAC đều

Cho đường tròn tâm O, bán kính R, đường kính AB, vẽ đường tròn tâm I, đường kính OA. a. Chm 2 đường tròn tâm O và tâm I tiếp xúc nhau, b. Dây AC của đường tròn tâm O cắt tâm I tại D. Chm ID//OC. c. Biết AC = R căn 3 . Tính theo R , diện tích ODCB
a:
I nằm giữa O và A
=>OI+IA=OA
=>OI=OA-AI
=R-R'
=>(O) với (I) tiếp xúc nhau tại A
b: ΔIAD cân tại I
=>góc IAD=góc IDA
=>góc IDA=góc OAC
ΔOAC cân tại O
=>góc OAC=góc OCA
=>góc IDA=góc OCA
mà hai góc này đồng vị
nên ID//OC
c: Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó; ΔACB vuông tại C
Xét ΔACB vuông tại C có cos CAB=AC/AB=1/2*căn 3
=>góc CAB=30 độ
CB=căn AB^2-AC^2=R/2
\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{R\sqrt{3}}{2}\cdot\dfrac{1}{2}R=\dfrac{R^2\sqrt{3}}{8}\)
Xét ΔADO vuông tại D và ΔACB vuông tại C có
góc DAO chung
Do đó: ΔADO đồng dạng với ΔACB
=>\(\dfrac{S_{ADO}}{S_{ACB}}=\left(\dfrac{AO}{AB}\right)^2=\left(\dfrac{1}{4}\right)\)
=>\(S_{ODCB}=\dfrac{3}{4}\cdot S_{ACB}=\dfrac{3}{4}\cdot\dfrac{R^2\sqrt{3}}{8}=\dfrac{3\cdot\sqrt{3}\cdot R^2}{32}\)