giải bpt bậc hai : x2-7x+22≤0
IH
Những câu hỏi liên quan
Cho phương trình bậc hai: x²-7x+m=0 a) Giải phương trình, m = 1 b) Tìm giá trị m để phương trình (1) có 2 nghiệm x1 và x2 thoả mãn: x1²+x2²=29
a, Thay \(m=1\) vào \(\left(1\right)\)
\(\Rightarrow x^2-7x+1=0\\ \Delta=\left(-7\right)^2-4.1.1=45\\ \Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{7+3\sqrt{5}}{2}\\x_2=\dfrac{7-3\sqrt{5}}{2}\end{matrix}\right.\)
b, \(\Delta=\left(-7\right)^2-4.m=49-4m\)
phương trình cs nghiệm \(49-4m\ge0\\ \Rightarrow m\le\dfrac{49}{4}\)
Áp dụng hệ thức vi ét
\(\left\{{}\begin{matrix}x_1+x_2=7\\x_1x_2=m\end{matrix}\right.\)
\(x^2_1+x^2_2=29\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\\ \Leftrightarrow7^2-2.m-29=0\\ \Leftrightarrow20-2m=0\\ \Rightarrow m=10\left(t/m\right)\)
Vậy \(m=10\)
Đúng 1
Bình luận (0)
Giải hệ bpt bậc nhất hai ẩn:
y - 2 > 0
x + 1 <0
x2 +2x+4 >0 giải bpt
\(x^2+2x+4=x^2+2x+1+3=\left(x+1\right)^2+3>0\forall x\in R\)
Vậy BPT có tập nghiệm là \(R\)
Đúng 1
Bình luận (0)
\(\sqrt{7x+1}\) - \(\sqrt{3x-8}\) ≤ \(\sqrt{2x+7}\)
giải bpt đưa về bậc 2
ĐKXĐ: \(x\ge\frac{8}{3}\)
\(\Leftrightarrow\sqrt{7x+1}\le\sqrt{3x-8}+\sqrt{2x+7}\)
\(\Leftrightarrow7x+1\le5x-1+2\sqrt{6x^2+5x-56}\)
\(\Leftrightarrow x+1\le\sqrt{6x^2+5x-56}\)
\(\Leftrightarrow x^2+2x+1\le6x^2+5x-56\)
\(\Leftrightarrow5x^2+3x-57\ge0\)
Nghiệm xấu quá \(x\ge\frac{-3+\sqrt{1149}}{10}\)
Đúng 0
Bình luận (0)
Giải bpt sau
(x - 1)(x2 - 7x + 6) > 0
Giải các bất phương trình bậc hai sau:
a) \(15{x^2} + 7x - 2 \le 0\)
b) \( - 2{x^2} + x - 3 < 0\)
a) Tam thức bậc hai \(f\left( x \right) = 15{x^2} + 7x - 2\) có hai nghiệm phân biệt là \({x_1} = - \frac{2}{3};{x_2} = \frac{1}{5}\)
và có \(a = 15 > 0\) nên \(f\left( x \right) \le 0\) khi x thuộc đoạn \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
Vậy tập nghiệm của bất phương trình \(15{x^2} + 7x - 2 \le 0\) là \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
b) Tam thức bậc hai \(f\left( x \right) = - 2{x^2} + x - 3\) có \(\Delta = - 23 < 0\) và \(a = - 2 < 0\)
nên \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
Vậy bất phương trình \( - 2{x^2} + x - 3 < 0\) có tập nghiệm là \(\mathbb{R}\)
Đúng 0
Bình luận (0)
Giải phương trình bậc hai
A. X2 - 4x + 3 = 0
B. X2 - 4 = 0
C. X2 + 4x = 0
a) x2-4x+3=0
có Δ' = b'2-ac= 4-3=1 >0
nên phương trình có 2 nghiệm phân biệt: x1= 3; x2= 1
b) x2 -4=0
⇔ x2=4
⇔\(\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
c)x2+4x=0
⇔x (x+4)=0
⇔\(\left[{}\begin{matrix}x=0\\x+4=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
2x2 – 7x + 3 = 0
Phương trình bậc hai 2x2 – 7x + 3 = 0
Có: a = 2; b = -7; c = 3; Δ = b2 – 4ac = (-7)2 – 4.2.3 = 25 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
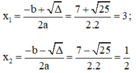
Vậy phương trình có hai nghiệm là 3 và 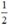
Đúng 0
Bình luận (0)
Gọi x1,x2 là nghiệm của phương trình x^2-7x+3=0
a/Lập phương trình bậc hai có hai nghiệm là 2x1-x2 và 2x2-x1
b/ tính giá trị A=|2x1-x2|+|2x2-x1|
a: \(a_1+a_2=2x_1-x_2+2x_2-x_1=x_1+x_2=7\)
\(a_1a_2=\left(2x_1-x_2\right)\left(2x_2-x_1\right)\)
\(=4x_1x_2-2x_1^2-2x_2^2+x_1x_2\)
\(=5x_1x_2-2\left(x_1^2+x_2^2\right)\)
\(=5x_1x_2-2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\)
\(=5\cdot3-2\left[7^2-2\cdot3\right]\)
\(=15-2\left[49-6\right]\)
\(=15-2\cdot43=15-86=-71\)
Do đó: Pt cần tìm là \(a^2-7a-71=0\)
b: \(A^2=\left[\left(2x_1-x_2\right)^2+\left(2x_2-x_1\right)^2+2\left(2x_1-x_2\right)\left(2x_2-x_1\right)\right]\)
\(=\left[4x_1^2-4x_1x_2+x_2^2+4x_2^2-4x_2x_1+x_1^2+2\cdot\left(-71\right)\right]\)
\(=\left[5\left(x_1^2+x_2^2\right)-8x_1x_2+2\cdot\left(-71\right)\right]\)
\(=\left[5\cdot43-8\cdot3-142\right]\)
\(=49\)
=>A=7 hoặc A=-7
Đúng 0
Bình luận (0)







