Tìm tập xác định: y = (3 - x) * sqrt(x - 1) + (2x + 2)/(x ^ 2 - 4x + 3)
§1. Hàm số
ĐKXĐ: \(\left\{{}\begin{matrix}x-1>=0\\x^2-4x+3< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=1\\\left(x-1\right)\left(x-3\right)< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>1\\x< >3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
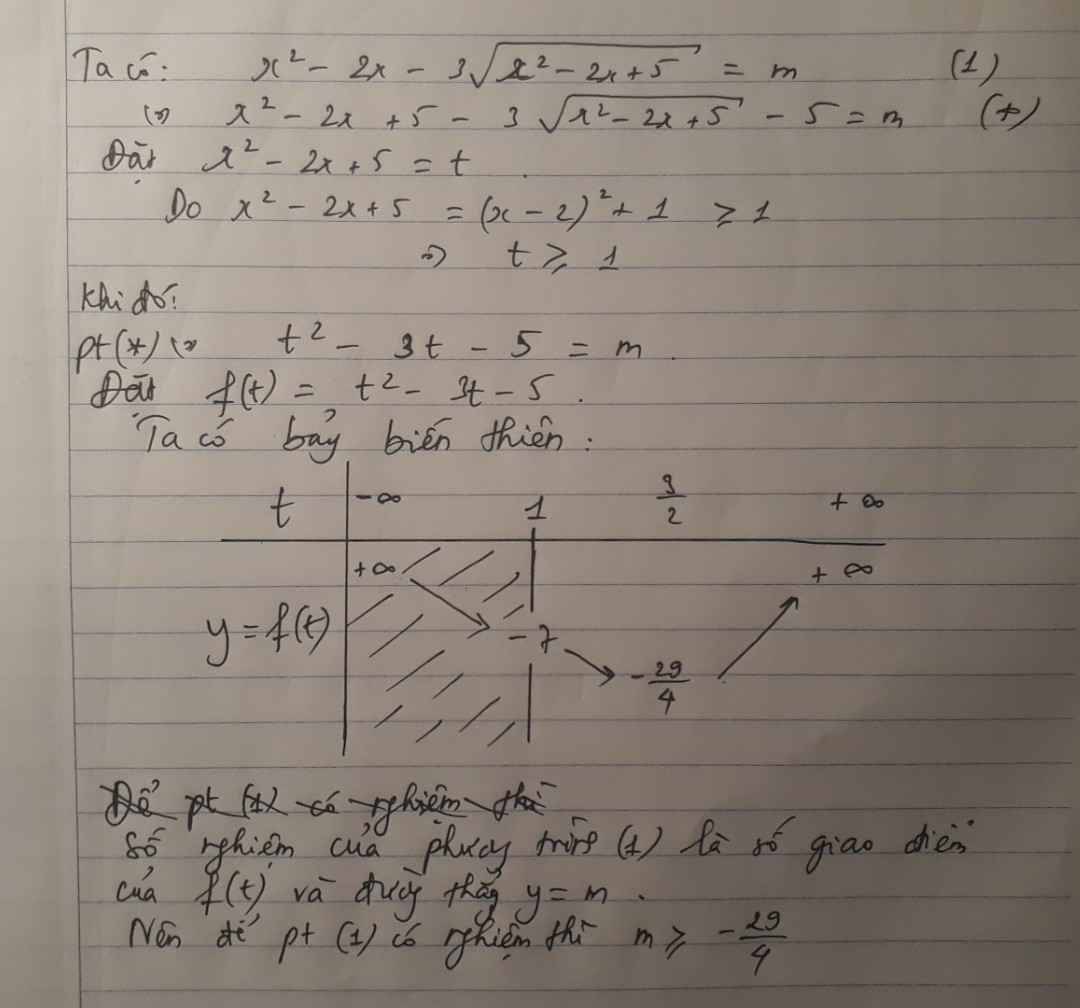
Tìm m : \(x^2-2x-3\sqrt{x^2-2x+5}=m\) có nghiệm ( dùng phương pháp bảng biến thiên, đồ thị )
Mình cảm ơn ạ !
hàm số y=\(\left\{{}\begin{matrix}\sqrt{x+1},x\ge-1\\2x^2-x+2,x< -1\end{matrix}\right.\) có tập xác định
cho mệnh đề chứa biến ''x2 - 3x +2 >0'' Hãy xác định tính đúng sai của các mệnh đề có được khi cho biến x nhận các giá trị sau đây a) x= 2 b) x= 0 c) x= 0,5 d) x= -1
Cho hàm số y=-x^2+bx-4 (1) Tìm b biết đồ thị hàm số (1) có trục đối xứng là đường thẳng x=5/2 Vẽ đồ thị hàm số (1) với b=5
Xem chi tiết
1: Theo đề, ta có:
-b/2*(-1)=5/2
=>-b/-2=5/2
=>b=5
2: y=-x^2+5x-4
Đúng 0
Bình luận (0)
Vẽ đồ thị của hàm số y = x ^ 2 - 2x + 2 và nêu các khoảng đồng biến,nghịch biến
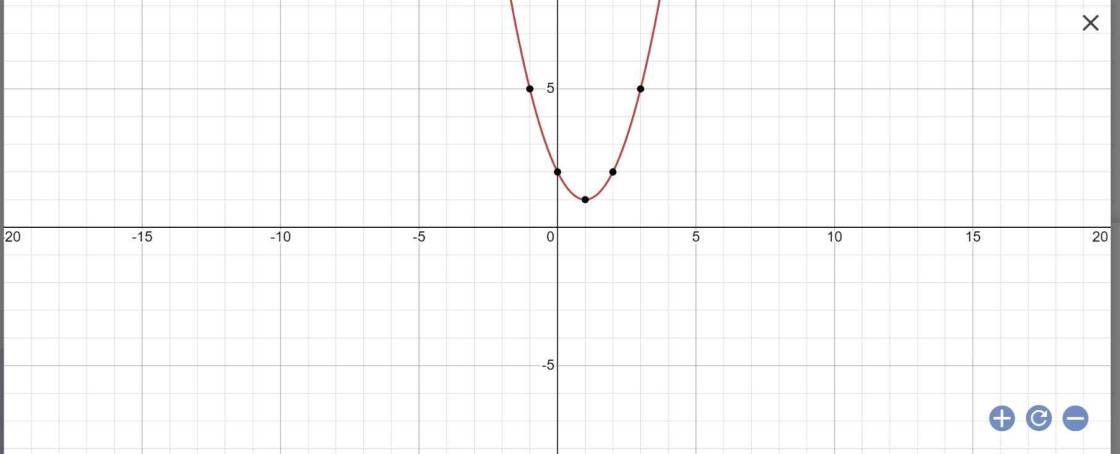
Tọa độ đỉnh là I(1;1)
mà a=1>0
nên hàm số đồng biến khi \(x\in\left(1;+\infty\right)\) và nghịch biến khi \(x\in\left(-\infty;1\right)\)
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số 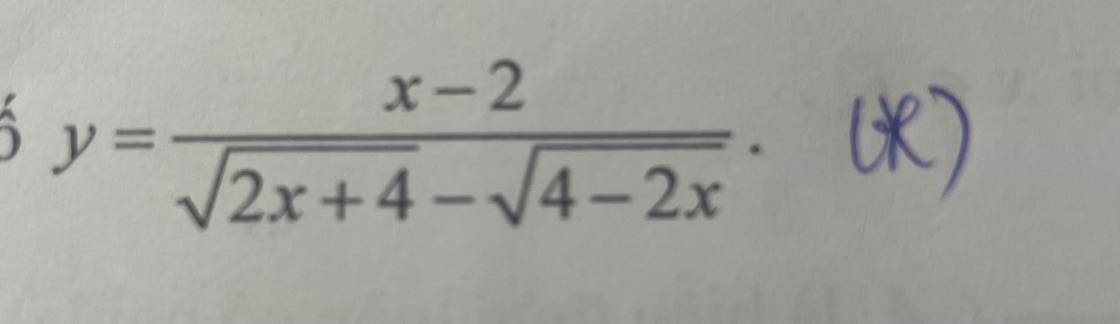
Đk: 2x + 4 > 0 và 4 - 2x > 0
=> x > -2 và x < 2
=> TXĐ: D = (-2;2)
Đúng 0
Bình luận (0)
H/s xác định `<=>{(2x+4 >= 0),(4-2x >= 0),(2x+4 ne 4-2x):}`
`<=>{(x >= -2),(x <= 2),(x ne 0):}<=>-2 <= x <= 2;x ne 0`
`=>TXĐ: D=[-2;2]\\{0}`
Đúng 0
Bình luận (0)
1. Tìm TXĐ, TGT của hàm số: y=\(\sqrt{x+2}+\sqrt{2-x}\)
`@` H/s xác định `<=>{(x+2 >= 0),(2-x >= 0):}<=>{(x >= -2),(x <= 2):}<=>-2 <= x <= 2`
`=>TXĐ: D=[-2;2]`
`@-2 <= x <= 2`
`<=>{(0 <= x+2 <= 4),(2 >= -x >= -2):}`
`<=>{(0 <= x+2 <= 4),(4 >= 2-x >= 0):}`
`<=>{(0 <= \sqrt{x+2} <= 2),(2 >= \sqrt{2-x} >= 0):}`
`=>TGT` là `[0;2]`
Đúng 3
Bình luận (0)
\(y=\sqrt{x+2}+\sqrt{2-x}\)
y có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x+2>0\\2-x>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x>2\end{matrix}\right.\)
TXD D = \(\left(2;+\infty\right)\)
Đúng 0
Bình luận (1)
\(đk\left\{{}\begin{matrix}x+2\ge0\\2-x\ge0\end{matrix}\right.=>\left\{{}\begin{matrix}x\ge-2\\x\le2\end{matrix}\right.\)
\(=>TXĐ:\left[-2;2\right]\)
Đúng 2
Bình luận (1)
1. Cho y=\(\sqrt{2x-m}\) . Tìm m để hàm số xác định trên [2;+∞)
hàm số xác định
\(2x-m\ge0\\ =>x\ge\dfrac{m}{2}\)
=> Tập xác định : \([\dfrac{m}{2};+\infty)\)
Để hàm số xác định trên đoạn \([2;+\infty)\)
\(2< \dfrac{m}{2}\\ =>m>4\)
Đúng 4
Bình luận (1)
1. Cho y=\(\dfrac{\sqrt{3x-5m+6}}{x+m-1}\) . Tìm m để hàm số xác định trên (0;m)