\(h\overrightarrow{a}+k\overrightarrow{b}=\left(2h;4h\right)+\left(3k;-5k\right)=\left(2h+3k;4h-5k\right)\)

\(\overrightarrow{u}=h\overrightarrow{a}+k\overrightarrow{b}\Leftrightarrow\left\{{}\begin{matrix}2h+3k=8\\4h-5k=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}h=1\\k=2\end{matrix}\right.\)

a) \(\overrightarrow{a}.\overrightarrow{b}=6\left(1-c\right)\)

b) \(\overrightarrow{a}.\overrightarrow{b}=-21\)

c) \(\overrightarrow{a}.\overrightarrow{b}=0\)

a) Ta thấy \(4 = ( - 2).( - 2); - 6 = ( - 2).3 \Rightarrow \overrightarrow a  =  - 2\overrightarrow b \)

\( - 2 < 0\) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng (đpcm)

b) Ta thấy \( - 8 = 4.( - 2);12 = 4.3 \Rightarrow \overrightarrow b  = 4\overrightarrow a \)

\(4 > 0\) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng  (đpcm)

c) Ta thấy \(0 =  - 1.0;4 = ( - 1).( - 4) \Rightarrow \overrightarrow a  =  - \overrightarrow b \)

Suy ra hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đối nhau (đpcm)

CHọn A

Lời giải:
Xét hai vecto bất kỳ  \(\overrightarrow{AB}, \overrightarrow{CD}\). Kẻ vecto $\overrightarrow{CT}$ sao cho $\overrightarrow{CT}=\overrightarrow{BA}$

Ta có:

\(|\overrightarrow{AB}+\overrightarrow{CD}|=|\overrightarrow{TC}+\overrightarrow{CD}|=|\overrightarrow{TD}|\)

\(|\overrightarrow{AB}|+|\overrightarrow{CD}|=|\overrightarrow{TC}|+|\overrightarrow{CD}|\)

Mà theo bđt tam giác thì:

\(|\overrightarrow{TC}+\overrightarrow{CD}|\geq |\overrightarrow{TD}|\Rightarrow |\overrightarrow{AB}|+\overrightarrow{CD}|\geq |\overrightarrow{AB}+\overrightarrow{CD}|\)

Dấu "=" xảy ra khi \(T, C,D\) thẳng hàng và $C$ nằm giữa $T,D$

$\Leftrightarrow \overrightarrow{TC}, \overrightarrow{CD}$ cùng hướng 

$\Leftrightarrow \overrightarrow{AB}, \overrightarrow{CD}$ cùng hướng

Vậy với $\overrightarrow{a}, \overrightarrow{b}$ bất kỳ thì $|\overrightarrow{a}|+|\overrightarrow{b}|\geq |\overrightarrow{a}+\overrightarrow{b}|$. Dấu "=" xảy ra khi $\overrightarrow{a}, \overrightarrow{b}$ cùng hướng.

------------------

Áp dụng vào bài toán:

\(|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}|\leq |\overrightarrow{a}+\overrightarrow{b}|+|\overrightarrow{c}|\leq |\overrightarrow{a}|+|\overrightarrow{b}|+|\overrightarrow{c}|\)

Dấu "=" xảy ra khi \(\overrightarrow{a}, \overrightarrow{b}\) cùng hướng và \(\overrightarrow{a}+\overrightarrow{b}, \overrightarrow{c}\) cùng hướng 

\(\Leftrightarrow \overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\) cùng hướng 

Tính \(\overrightarrow{a}.\overrightarrow{b}\) hả bạn?

\(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|cos\left(\overrightarrow{a};\overrightarrow{b}\right)=2.\sqrt{3}.cos30^0=3\)

Đặt \(A=\left|\overrightarrow{a}+\overrightarrow{b}\right|\Rightarrow A^2=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.cos\left(\overrightarrow{a};\overrightarrow{b}\right)\)

\(=2^2+3+2.2.\sqrt{3}.cos30^0=13\)

\(\Rightarrow\left|\overrightarrow{a}+\overrightarrow{b}\right|=\sqrt{13}\)

Ta có:

\(\overrightarrow{a}+\overrightarrow{b}+3\overrightarrow{c}=\overrightarrow{0}\Leftrightarrow\overrightarrow{a}+\overrightarrow{b}=-3\overrightarrow{c}\Leftrightarrow\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=9\overrightarrow{c}^2\)

<=> \(\overrightarrow{a}^2+\overrightarrow{b}^2+2\overrightarrow{a}\overrightarrow{b}=9\overrightarrow{c}^2\)

<=> \(\overrightarrow{a}\overrightarrow{b}=\dfrac{9z^2-x^2-y^2}{2}\)

Tương tự ta có: \(\overrightarrow{b}+3\overrightarrow{c}=-\overrightarrow{a}\) <=> \(\left(\overrightarrow{b}+3\overrightarrow{c}\right)^2=\overrightarrow{a}^2\) 

<=> \(\overrightarrow{b}.\overrightarrow{c}=\dfrac{x^2-y^2-9z^2}{2}\)

Và lại có : \(\overrightarrow{a}\overrightarrow{c}=\dfrac{y^2-x^2-9z^2}{2}\)

Suy ra: A=\(\dfrac{9z^2-x^2-y^2}{2}+\dfrac{x^2-y^2-9z^2}{2}+\dfrac{y^2-x^2-9z^2}{2}=\dfrac{3z^2-z^2-y^2}{2}\)

Ta có

\(\begin{array}{l}\overrightarrow {FE}  = ({x_E} - {x_F};{y_E} - {y_F}) = (9 - 8;9 - ( - 7)) = (1;16)\\\overrightarrow {FG}  = ({x_G} - {x_F};{y_G} - {y_F}) = (0 - 8;( - 6) - ( - 7)) = ( - 8;1)\\\overrightarrow {EG}  = ({x_G} - {x_E};{y_G} - {y_E}) = (0 - 9;( - 6) - 9) = ( - 9; - 15)\end{array}\)

giả sử tam giác ABC \(\overrightarrow{BC}\)=\(\overrightarrow{a}\) \(\overrightarrow{AC}\)= \(\overrightarrow{b}\) \(\overrightarrow{AB}\)=\(\overrightarrow{c}\)

theo đề ta có

BC-AC< AB < BC+AC

Tham khảo:

a) Ta có: \(\overrightarrow b  = \left( {4; - 1} \right)\) và \(\overrightarrow a  = 3.\overrightarrow i  - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)\)

\( \Rightarrow 2\;\overrightarrow a  - \overrightarrow b  = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)\)

Lại có: M (-3; 6), N(3; -3)

\( \Rightarrow \overrightarrow {MN}  = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)\)

Dễ thấy:\(\left( {6; - 9} \right) = 3.\left( {2; - 3} \right)\) \( \Rightarrow \overrightarrow {MN}  = 3\left( {2\;\overrightarrow a  - \overrightarrow b } \right)\)

b) Ta có: \(\overrightarrow {OM}  = \left( { - 3;6} \right)\) ( do M(-3; 6)) và \(\overrightarrow {ON}  = \left( {3; - 3} \right)\) (do N (3; -3)).

Hai vectơ này không cùng phương (vì \(\frac{{ - 3}}{3} \ne \frac{6}{{ - 3}}\)).

Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.

Vậy chúng không thẳng hàng.

c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi \(\overrightarrow {OM}  = \overrightarrow {PN} \).

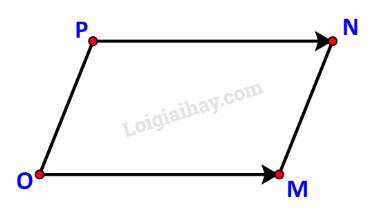
Do \(\overrightarrow {OM}  = \left( { - 3;6} \right),\;\overrightarrow {PN}  = \left( {3 - x; - 3 - y} \right)\)  nên

\(\overrightarrow {OM}  = \overrightarrow {PN}  \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 =  - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y =  - 9\end{array} \right.\)

Vậy điểm cần tìm là P (6; -9).