Cho phân thức ; Tìm giá trị của x,y,z để phân thức xác định:
\(A=\dfrac{\left(5x^2+5y^2+5z^2\right)\left(x+y+z\right)^2+5\left(xy+yz+zx\right)^2}{\left(5x+5y+5z\right)^2-\left(25xy+25yz+25zx\right)}\)
AH
Những câu hỏi liên quan
Đố. Cho phân thức
2
x
+
1
x
3
-
3
Đố em tìm được một phân thức mà khi lấy phân thức đã cho trừ đi phân thức phải tìm thì được một phân thức bằng phân thức đối của phân thức đã cho.
Đọc tiếp
Đố. Cho phân thức
2 x + 1 x 3 - 3
Đố em tìm được một phân thức mà khi lấy phân thức đã cho trừ đi phân thức phải tìm thì được một phân thức bằng phân thức đối của phân thức đã cho.
Gọi phân thức cần tìm là A.
Lấy phân thức đã cho trừ đi phân thức phải tìm ta được: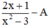 
Phân thức đối của phân thức đã cho là: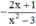 
Theo đề bài ta có: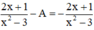 
Cộng cả hai vế với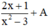 
ta có :
Đúng 0
Bình luận (0)
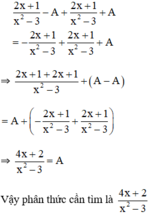
Đố :
Cho phân thức \(\dfrac{2x+1}{x^2-3}\). Đố em tìm được một phân thức mà khi lấy phân thức đã cho trừ đi phân thức phải tìm thì được một phân thức bằng phân thức đối của phân thức đã cho ?
Cho phân thức
.
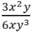Hãy chia tử và mẫu của phân thức này cho 3xy rồi so sánh phân thức vừa nhận được với phân thức đã cho.
3x2y : 3xy = x
6xy3 : 3xy = 2y2
Mà: 3x2y . 2y2 = 6x2y3
6xy3.x = 6x2y3
Đúng 0
Bình luận (0)
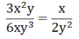
Cho phân thức x/3. Hãy nhân tử và mẫu của phân thức này với x + 2 rồi so sánh phân thức vừa nhận được với phân thức đã cho.
x.(x + 2) = x2 + 2x
3.(x +2) = 3x + 6
⇒ x(3x + 6) = 3(x2 + 2x) = 3x2 + 6x
Đúng 0
Bình luận (0)
H24
16 tháng 11 2021 lúc 13:11
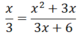
Cho phân thức x/3. Hãy nhân tử và mẫu của phân thức này với x+2 rồi so sánh phân thức vừa nhận được với phân thức đã cho
Phân thức nhận được bằng phân thức đã cho
Đúng 1
Bình luận (0)
Cho phân thức a) Với giá trị nào của x thì giá trị của phân thức được xác định ? b) Chứng tỏ phân thức rút gọn của phân thức đã cho là c) Để tính giá trị của phân thức đã cho tại x 2 và x -1, bạn Thắng đã làm như sau: - Với x 2, phân thức đã cho có giá trị là - Với x -1, phân thức đã cho có giá trị là Em có đồng ý không ? Nếu không, em hãy chỉ ra chỗ mà em cho là sai. Theo em, với những giá trị nào của biến thì có thể tính được giá trị của phân thức đã cho bằng cách tính giá trị của phân...
Đọc tiếp
Cho phân thức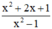 
a) Với giá trị nào của x thì giá trị của phân thức được xác định ?
b) Chứng tỏ phân thức rút gọn của phân thức đã cho là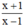 
c) Để tính giá trị của phân thức đã cho tại x = 2 và x = -1, bạn Thắng đã làm như sau:
- Với x = 2, phân thức đã cho có giá trị là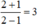 
- Với x = -1, phân thức đã cho có giá trị là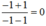 
Em có đồng ý không ? Nếu không, em hãy chỉ ra chỗ mà em cho là sai.
Theo em, với những giá trị nào của biến thì có thể tính được giá trị của phân thức đã cho bằng cách tính giá trị của phân thức rút gọn ?
a) Phân thức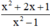 
xác định
⇔ x2 – 1 ≠ 0
⇔ (x – 1)(x + 1) ≠ 0
⇔ x – 1 ≠ 0 và x + 1 ≠ 0
⇔ x ≠ ±1
Vậy phân thức xác định với mọi x ≠ ±1
b) Với x ≠ ±1, ta có:
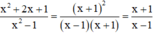
c) + Với x = 2, bạn Thắng tính giá trị biểu thức đúng.
+ Với x = -1, phân thức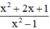 
không xác định nên không thể tính giá trị biểu thức nên bạn Thắng tính sai.
+ Để tính giá trị của phân thức bằng cách tính giá trị của phân thức rút gọn, ta phải đảm bảo giá trị của biến thỏa mãn điều kiện xác định.
Đúng 0
Bình luận (0)
Cho phân thức m n là phân thức tối giản. Chứng minh phân thức m m + n là phân thức tối giản
Hướng dẫn giải:
Giả sử m, n là các số nguyên và ƯCLN(m, n) = 1 (vì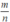 
tối giản)
nếu d là ước chung m của m + n thì:
(m + n) d và m d
⇒ [(m + n) – m ] = n d
⇒ d ∈ ƯC (m,n) ⇒ d = 1(vì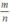 
tối giản) .
Vậy nếu phân thức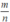 
là phân thức tối giản thì phân thức 
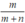cũng là phân thức tối giản.
Đúng 0
Bình luận (0)
Cho phân thức ( 2 x ) ( x + 2 ) . Nhân cả tử và mẫu với đa thức ( x - 1 ), so sánh phân thức nhận được với phân thức đã cho ?
Ta có phân thức mới là
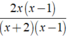
Ta có
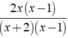
= (2x)/(x + 2)
vì 2x( x - 1 ).( x + 2 ) = 2x.( x + 2 )( x - 1 ).
Đúng 0
Bình luận (0)
Cho phân thức \(\frac{x-2}{x+2}\) với \(x\)≠\(-2\). Biến đổi phân thức đã cho thành một phân thức bằng nó và có tử thức là đa thức \(A=x^2-4\)
\(\dfrac{x-2}{x+2}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x+2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-2^2}{\left(x+2\right)^2}\)
\(=\dfrac{x^2-4}{x^2+4x+4}\)
Vậy đã biến đổi phân thức thành một phân thức bằng nó và có tử bằng với đa thức: \(A=x^2-4\)
Đúng 1
Bình luận (1)
Cho đa thức
A
2
x
3
+
x
2
−
13
x
+
6
và hai phân thức:
x
2
x
2
+
5
x
−
3
,
x
+
2...
Đọc tiếp
Cho đa thức A = 2 x 3 + x 2 − 13 x + 6 và hai phân thức: x 2 x 2 + 5 x − 3 , x + 2 x 2 + x − 6 với x ≠ − 3 ; x ≠ 1 2 và x ≠ 2 .
a) Chia đa thức A lần lượt cho các mẫu thức của hai phân thức đã cho.
b) Quy đồng mẫu thức của hai phân thức đã cho.
