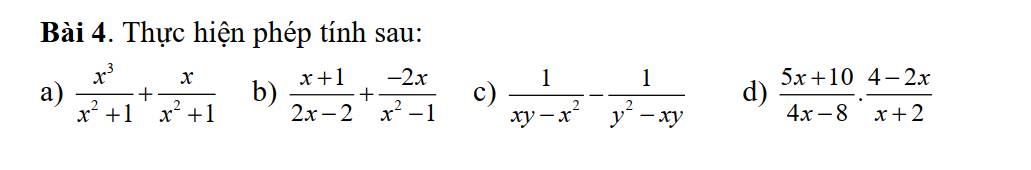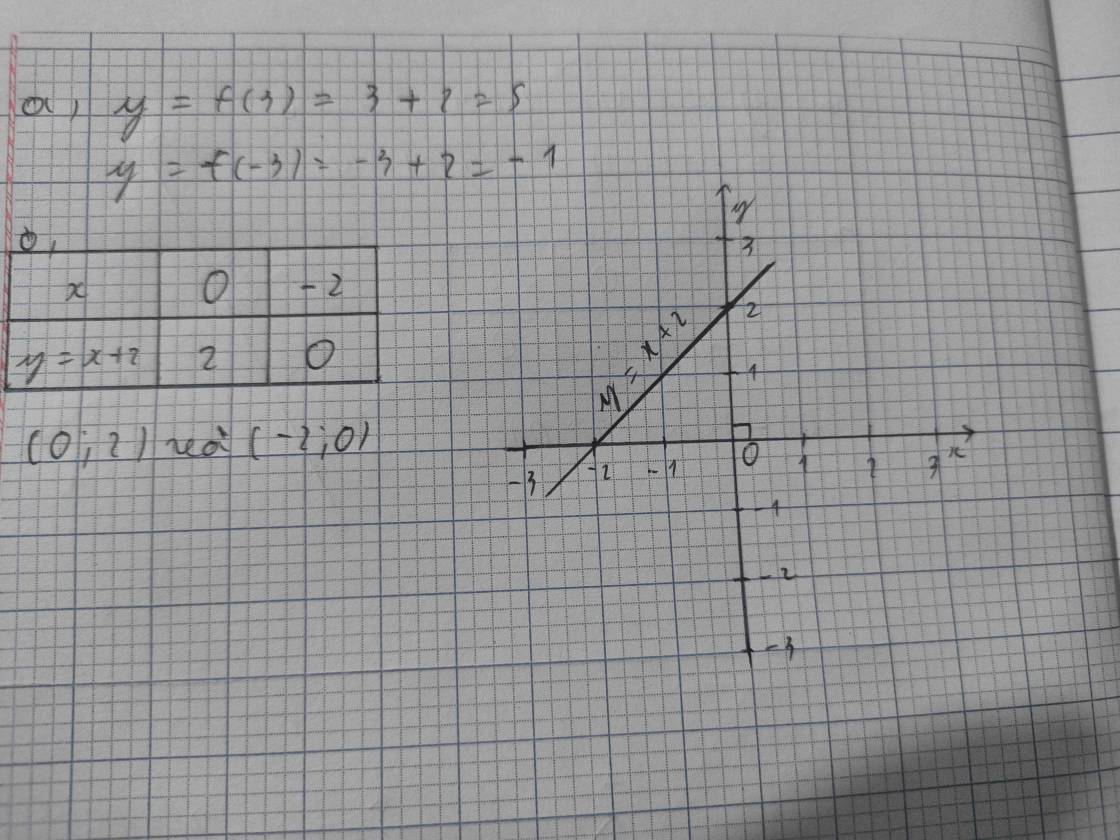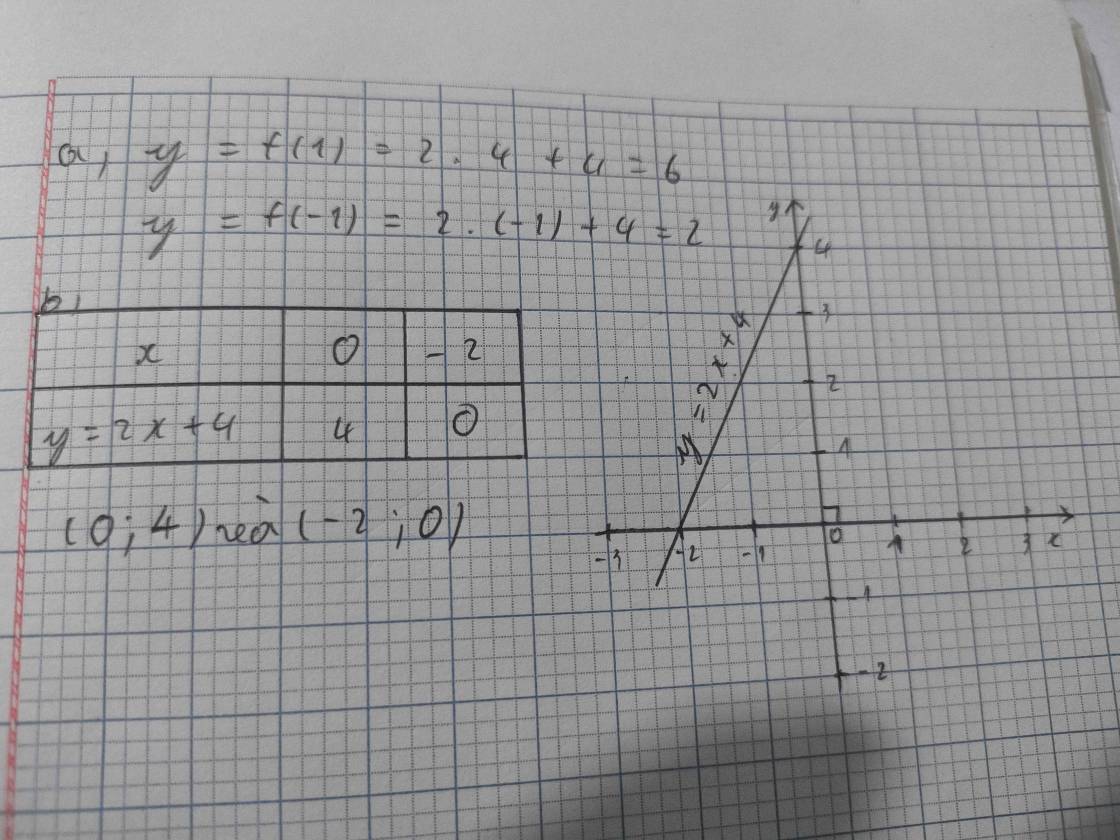Ôn tập: Phân thức đại số

1: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)

2: \(P=\dfrac{x^2+2x}{2x+10}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)

\(=\dfrac{x^2+2x}{2\left(x+5\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)

\(=\dfrac{x\left(x^2+2x\right)+2\left(x+5\right)\left(x-5\right)+50-5x}{2x\left(x+5\right)}\)

\(=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)

\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)

3: \(P=\dfrac{1}{4}\)

=>\(\dfrac{x-1}{2}=\dfrac{1}{4}\)

=>\(x-1=\dfrac{1}{2}\)

=>\(x=\dfrac{3}{2}\left(nhận\right)\)

4: P<0

=>\(\dfrac{x-1}{2}< 0\)

=>x-1<0

=>x<1

Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< 1\\x\notin\left\{0;-5\right\}\end{matrix}\right.\)

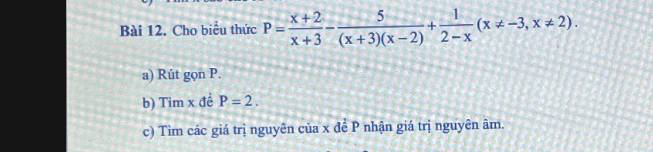
a) \(P=\dfrac{x+2}{x+3}-\dfrac{5}{\left(x+3\right)\left(x-2\right)}+\dfrac{1}{2-x}\left(x\ne-3;x\ne2\right)\)

\(P=\dfrac{x+2}{x+3}-\dfrac{5}{\left(x+3\right)\left(x-2\right)}-\dfrac{1}{x-2}\)

\(P=\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x+3\right)\left(x-2\right)}-\dfrac{5}{\left(x+3\right)\left(x-2\right)}-\dfrac{x+3}{\left(x+3\right)\left(x-2\right)}\)

\(P=\dfrac{x^2-4-5-x-3}{\left(x+3\right)\left(x-2\right)}\)

\(P=\dfrac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}\)

\(P=\dfrac{x^2+3x-4x-12}{\left(x+3\right)\left(x-2\right)}\)

\(P=\dfrac{\left(x+3\right)\left(x-4\right)}{\left(x+3\right)\left(x-2\right)}\)

\(P=\dfrac{x-4}{x-2}\)

b) \(P=2\) khi:

\(\dfrac{x-4}{x-2}=2\Leftrightarrow x-4=2\left(x-2\right)\Leftrightarrow x-4=2x-4\)

\(\Leftrightarrow2x-x=-4+4\Leftrightarrow x=0\left(tm\right)\)

c) Ta có: \(P=\dfrac{x-4}{x-2}=\dfrac{x-2-2}{x-2}=1-\dfrac{2}{x-2}\)

Do P nguyên âm \(\Rightarrow P< 0\Rightarrow\dfrac{2}{x-2}>1\)

\(\Leftrightarrow\dfrac{4-x}{x-2}>0\) 

TH1: \(\left\{{}\begin{matrix}4-x>0\\x-2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 4\\x>2\end{matrix}\right.\Leftrightarrow2< x< 4\) 

TH2: \(\left\{{}\begin{matrix}4-x< 0\\x-2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>4\\x< 2\end{matrix}\right.\Leftrightarrow x\in\varnothing\) 

Mà P lại là 1 số nguyên nên các số nguyên x thỏa mãn là \(x\in\left\{4;0;3;1\right\}\) 

Vậy để P là số nguyên âm và x là số nguyên thì \(\left\{{}\begin{matrix}2< x< 4\\x\in\left\{4;0;3;1\right\}\end{matrix}\right.\Leftrightarrow x=1\)

\(\dfrac{x+3}{x^2-1}-\dfrac{1}{x^2+x}\\ =\dfrac{x+3}{\left(x-1\right)\cdot\left(x+1\right)}-\dfrac{1}{x\cdot\left(x+1\right)}\\ =\dfrac{x\cdot\left(x+3\right)}{x\cdot\left(x-1\right)\cdot\left(x+1\right)}-\dfrac{x-1}{x\cdot\left(x-1\right)\cdot\left(x+1\right)}\)

\(=\dfrac{x^2+3x-x+1}{x\cdot\left(x-1\right)\cdot\left(x+1\right)}\\ =\dfrac{x^2+2x+1}{x\left(x-1\right)\left(x+1\right)}\\ =\dfrac{\left(x+1\right)^2}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x\left(x-1\right)}\)

Ta có biểu thức \(\dfrac{x}{x^2+3x}\) 

ĐKXĐ: \(x^2+3x\ne0\)

\(\Leftrightarrow x\left(x+3\right)\ne0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x+3\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne-3\end{matrix}\right.\)

Bài 1:

1: \(P=\left(\dfrac{4}{x-1}-\dfrac{7x+5}{x^3-1}\right):\left(1-\dfrac{x-4}{x^2+x+1}\right)\)

\(=\left(\dfrac{4}{x-1}-\dfrac{7x+5}{\left(x-1\right)\left(x^2+x+1\right)}\right):\dfrac{x^2+x+1-x+4}{x^2+x+1}\)

\(=\dfrac{4\left(x^2+x+1\right)-7x-5}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^2+x+1}{x^2+5}\)

\(=\dfrac{4x^2+4x+4-7x-5}{\left(x-1\right)\left(x^2+5\right)}\)

\(=\dfrac{4x^2-3x-1}{\left(x-1\right)\left(x^2+5\right)}\)

\(=\dfrac{4x^2-4x+x-1}{\left(x-1\right)\left(x^2+5\right)}=\dfrac{\left(x-1\right)\left(4x+1\right)}{\left(x-1\right)\left(x^2+5\right)}\)

\(=\dfrac{4x+1}{x^2+5}\)

2: \(x^3-x^2-4=0\)

=>\(x^3-2x^2+x^2-4=0\)

=>\(x^2\left(x-2\right)+\left(x-2\right)\left(x+2\right)=0\)

=>\(\left(x-2\right)\left(x^2+x+2\right)=0\)

mà \(x^2+x+2=x^2+x+\dfrac{1}{4}+\dfrac{7}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}>\dfrac{7}{4}>0\forall x\)

nên x-2=0

=>x=2

Thay x=2 vào P, ta được:

\(P=\dfrac{4\cdot2+1}{2^2+5}=\dfrac{9}{9}=1\)

3: \(P=\dfrac{4x+1}{x^2+5}\)

=>\(P-1=\dfrac{4x+1-x^2-5}{x^2+5}=\dfrac{-x^2+4x-4}{x^2+5}\)

\(=-\dfrac{\left(x-2\right)^2}{x^2+5}< =0\forall x\) thỏa mãn ĐKXĐ

=>\(P< =1\forall x\) thỏa mãn ĐKXĐ

Dấu '=' xảy ra khi x-2=0

=>x=2

Bài 2:

1: \(2x^2+3y^2+4x=19\)

=>\(\left(2x^2+4x+2\right)+3y^2-21=0\)

=>\(2\left(x+1\right)^2+3y^2=21\)

mà x,y nguyên

nên \(\left[2\left(x+1\right)^2;3y^2\right]\in\left(18;3\right)\)

=>\(\left[\left(x+1\right)^2;y^2\right]\in\left(9;1\right)\)

=>\(\left(x+1;y\right)\in\left\{\left(3;1\right);\left(-3;-1\right);\left(3;-1\right);\left(-3;1\right)\right\}\)

=>\(\left(x;y\right)\in\left\{\left(2;1\right);\left(-4;-1\right);\left(2;-1\right);\left(-4;1\right)\right\}\)

Ta có:

\(3x-3=3\left(x-1\right)\)

\(4-4x=-4\left(x-1\right)\)

\(x^2-1=\left(x-1\right)\left(x+1\right)\)

\(\Rightarrow\) MTC là \(3.\left(-4\right).\left(x-1\right)\left(x+1\right)=-12\left(x-1\right)\left(x+1\right)\)

Do đó:

\(\dfrac{11x}{3x-3}=\dfrac{11x}{3\left(x-1\right)}=\dfrac{11x.\left(-4\right).\left(x+1\right)}{3\left(x-1\right).\left(-4\right)\left(x+1\right)}=\dfrac{-44x\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)

\(\dfrac{5}{4-4x}=\dfrac{5}{-4\left(x-1\right)}=\dfrac{5.3\left(x+1\right)}{-4\left(x-1\right).3\left(x+1\right)}=\dfrac{15\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)

\(\dfrac{2x}{x^2-1}=\dfrac{2x}{\left(x-1\right)\left(x+1\right)}=\dfrac{2x.\left(-12\right)}{-12\left(x-1\right)\left(x+1\right)}=\dfrac{-24x}{-12\left(x-1\right)\left(x+1\right)}\)

a: \(\dfrac{x^3}{x^2+1}+\dfrac{x}{x^2+1}\)

\(=\dfrac{x^3+x}{x^2+1}\)

\(=\dfrac{x\left(x^2+1\right)}{x^2+1}=x\)

b: 

ĐKXĐ: \(x\notin\left\{1;-1\right\}\)

\(\dfrac{x+1}{2x-2}+\dfrac{-2x}{x^2-1}\)

\(=\dfrac{x+1}{2\left(x-1\right)}-\dfrac{2x}{\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{\left(x+1\right)^2-4x}{2\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x-1\right)^2}{2\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{2\left(x-1\right)}\)

c: ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0;y\ne0\\x\ne y\end{matrix}\right.\)

\(\dfrac{1}{xy-x^2}-\dfrac{1}{y^2-xy}\)

\(=\dfrac{1}{x\left(y-x\right)}-\dfrac{1}{y\left(y-x\right)}\)

\(=\dfrac{y-x}{xy\left(y-x\right)}=\dfrac{1}{xy}\)

d: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)

\(\dfrac{5x+10}{4x-8}\cdot\dfrac{4-2x}{x+2}\)

\(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}\)

\(=\dfrac{5\cdot\left(-2\right)}{4}=-\dfrac{10}{4}=-\dfrac{5}{2}\)

a.

\(\dfrac{x^3}{x^2+1}+\dfrac{x}{x^2+1}=\dfrac{x^3+x}{x^2+1}=\dfrac{x\left(x^2+1\right)}{x^2+1}=x\)

b.

\(\dfrac{x+1}{2x-2}+\dfrac{-2x}{x^2-1}=\dfrac{x+1}{2\left(x-1\right)}-\dfrac{2x}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x+1\right)^2}{2\left(x-1\right)\left(x+1\right)}-\dfrac{4x}{2\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{x^2+2x+1-4x}{2\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x-1\right)^2}{2\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{2\left(x+1\right)}\)

c.

\(\dfrac{1}{xy-x^2}-\dfrac{1}{y^2-xy}=\dfrac{1}{x\left(y-x\right)}-\dfrac{1}{y\left(y-x\right)}=\dfrac{y}{xy\left(y-x\right)}-\dfrac{x}{xy\left(y-x\right)}\)

\(=\dfrac{y-x}{xy\left(y-x\right)}=\dfrac{1}{xy}\)

d.

\(\dfrac{5x+10}{4x-8}.\dfrac{4-2x}{x+2}=\dfrac{5\left(x+2\right)}{2\left(x-2\right)}.\dfrac{-2\left(x-2\right)}{x+2}=-5\)

ĐKXĐ: \(x\ne-\dfrac{1}{3}\)

\(A=\dfrac{\left(3x-1\right)^2}{3x+1}=\dfrac{9x^2-6x+1}{3x+1}\)

Để A là số nguyên thì \(9x^2-6x+1⋮3x+1\)

=>\(9x^2+3x-9x-3+4⋮3x+1\)

=>\(4⋮3x+1\)

=>\(3x+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(3x\in\left\{0;-2;1;-3;3;-5\right\}\)

=>\(x\in\left\{0;-\dfrac{2}{3};\dfrac{1}{3};-1;1-\dfrac{5}{3}\right\}\)

mà x nguyên

nên \(x\in\left\{0;1;-1\right\}\)