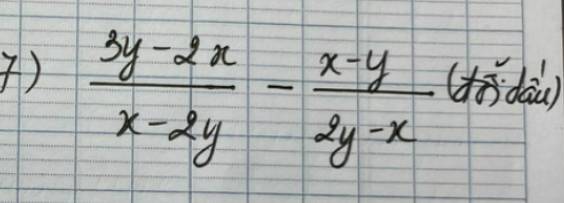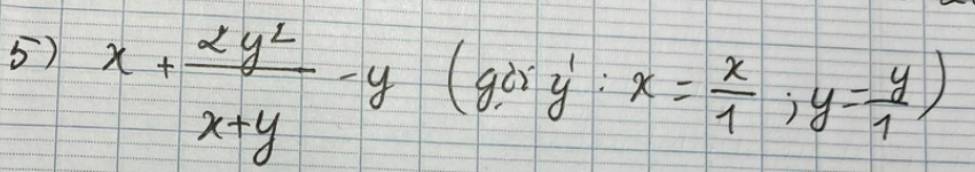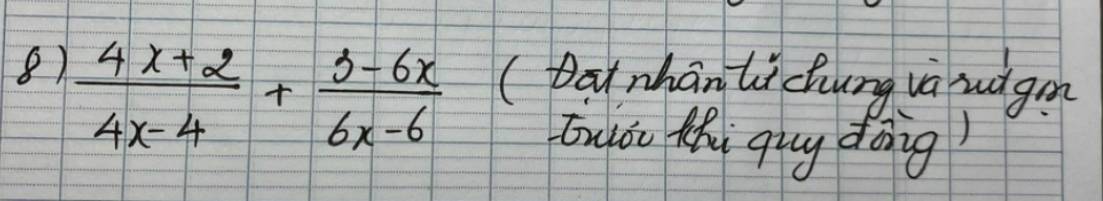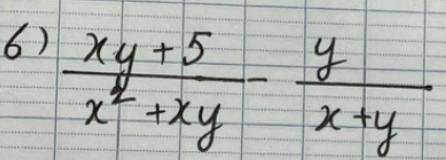
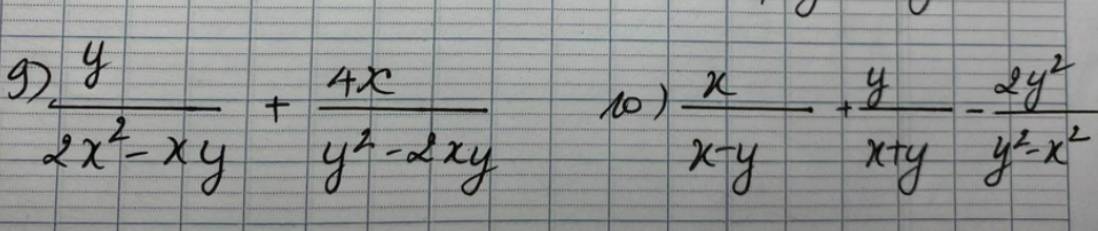
Bài 2: Tính chất cơ bản của phân thức
6) \(\dfrac{xy+5}{x^2+xy}-\dfrac{y}{x+y}\)
\(=\dfrac{xy+5}{x\left(x+y\right)}-\dfrac{xy}{x\left(x+y\right)}\)
\(=\dfrac{xy+5-xy}{x\left(x+y\right)}\)
\(=\dfrac{5}{x\left(x+y\right)}\)
\(=\dfrac{5}{x^2+xy}\)
9) \(\dfrac{y}{2x^2-xy}+\dfrac{4x}{y^2-2xy}\)
\(=\dfrac{y}{x\left(2x-y\right)}+\dfrac{4x}{y\left(y-2x\right)}\)
\(=\dfrac{y^2}{xy\left(2x-y\right)}-\dfrac{4x^2}{xy\left(2x-y\right)}\)
\(=-\dfrac{4x^2-y^2}{xy\left(2x-y\right)}\)
\(=-\dfrac{\left(2x-y\right)\left(2x+y\right)}{xy\left(2x-y\right)}\)
\(=-\dfrac{2x+y}{xy}\)
10) \(\dfrac{x}{x-y}+\dfrac{y}{x+y}-\dfrac{2y^2}{y^2-x^2}\)
\(=\dfrac{x\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{y\left(x-y\right)}{\left(x+y\right)\left(x-y\right)}+\dfrac{2y^2}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2+xy+xy-y^2+2y^2}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2+2xy+y^2}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{\left(x+y\right)^2}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x+y}{x-y}\)
Đúng 2
Bình luận (0)
7) \(\dfrac{3y-2x}{x-2y}-\dfrac{x-y}{2y-x}\)
\(=\dfrac{3y-2x}{x-2y}+\dfrac{x-y}{x-2y}\)
\(=\dfrac{3y-2x+x-y}{x-2y}\)
\(=\dfrac{2y-x}{x-2y}\)
\(=-\dfrac{x-2y}{x-2y}\)
\(=-1\)
5) \(x+\dfrac{2y^2}{x+y}-y\)
\(=\dfrac{x\left(x+y\right)}{x+y}+\dfrac{2y^2}{x+y}-\dfrac{y\left(x+y\right)}{x+y}\)
\(=\dfrac{x^2+xy+2y^2-xy-y^2}{x+y}\)
\(=\dfrac{x^2+y^2}{x+y}\)
8) \(\dfrac{4x+2}{4x-4}+\dfrac{3-6x}{6x-6}\)
\(=\dfrac{2\left(2x+1\right)}{2\left(2x-2\right)}+\dfrac{3\left(1-2x\right)}{3\left(2x-2\right)}\)
\(=\dfrac{2x+1}{2x-2}+\dfrac{1-2x}{2x-2}\)
\(=\dfrac{2x+1+1-2x}{2x-2}\)
\(=\dfrac{2}{2x-2}\)
\(=\dfrac{1}{x-1}\)
Đúng 1
Bình luận (0)
Khẳng định sau đúng hay sai? Vì sao?30xy2(x−y)45xy(x−y)22y3(x−y)
Đọc tiếp
Khẳng định sau đúng hay sai? Vì sao?
30xy2(x−y)45xy(x−y)2=2y3(x−y)
A/3y+1=9y²-6y+1/3y-1
\(a,3y+1=\dfrac{9y^2-6y+1}{3y-1}\\ \Leftrightarrow3y+1=\dfrac{\left(3y-1\right)^2}{3y-1}\\ \Leftrightarrow3y+1=3y-1\left(voli\right)??\)
Đúng 0
Bình luận (2)
m-n/2m=3m(m-n)²/6m²(m-n)
\(\dfrac{3m\left(m-n\right)^2}{6m^2\left(m-n\right)}=\dfrac{3m\cdot\left(m-n\right)\cdot\left(m-n\right)}{3m\left(m-n\right)\cdot2m}=\dfrac{m-n}{2m}\)
Đúng 0
Bình luận (0)
m²-2mn+n²/m²-n²=m-n/m+n
\(\dfrac{m^2-2mn+n^2}{m^2-n^2}=\dfrac{\left(m-n\right)^2}{\left(m-n\right)\left(m+n\right)}=\dfrac{m-n}{m+n}\)
Đúng 0
Bình luận (0)
a²+4ab+b²/a²-4b²=a+2b/a-2b
\(\dfrac{a^2+4ab+4b^2}{a^2-4b^2}=\dfrac{\left(a+2b\right)^2}{\left(a-2b\right)\left(a+2b\right)}=\dfrac{a+2b}{a-2b}\)
Đúng 1
Bình luận (0)
a-b/11=3a(a-b)²/33a²-3ab
\(\dfrac{3a\left(a-b\right)^2}{33a^2-3ab}=\dfrac{3a\left(a-b\right)^2}{3a\left(11a-b\right)}=\dfrac{\left(a-b\right)^2}{11a-b}\)
Đúng 1
Bình luận (0)
3m/m+n=3m(m-n)/n²-m²
\(\dfrac{3m\left(m-n\right)}{n^2-m^2}=\dfrac{3m\left(m-n\right)}{\left(n-m\right)\left(n+m\right)}=\dfrac{-3m}{m+n}\)
Đúng 0
Bình luận (0)
y-2/-y=8-y³/y(4+2y+y²)
\(\dfrac{8-y^3}{y\left(4+2y+y^2\right)}=\dfrac{\left(2-y\right)\left(4+2y+y^2\right)}{y\left(4+2y+y^2\right)}=\dfrac{2-y}{y}\)
=(y-2)/(-y)
Đúng 0
Bình luận (1)