3x2y : 3xy = x
6xy3 : 3xy = 2y2
Mà: 3x2y . 2y2 = 6x2y3
6xy3.x = 6x2y3
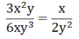
3x2y : 3xy = x
6xy3 : 3xy = 2y2
Mà: 3x2y . 2y2 = 6x2y3
6xy3.x = 6x2y3
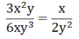
Cho phân thức x/3. Hãy nhân tử và mẫu của phân thức này với x + 2 rồi so sánh phân thức vừa nhận được với phân thức đã cho.
Cho phân thức ( 2 x ) ( x + 2 ) . Nhân cả tử và mẫu với đa thức ( x - 1 ), so sánh phân thức nhận được với phân thức đã cho ?
Ta có phân thức x x + 1 . Đổi dấu cả tử và mẫu ta được phân thức mới, so sánh phân thức mới với phân thức đã cho
Cho hai phân thức: 3 x 2 x + 5 v à x 2 - 25 6 x 3 Cũng làm như nhân hai phân số, hãy tử với tử và mẫu với mẫu của hai phân thức này để được một phân thức.
Cho các phân thức 1 a 2 − a − 2 và a a 2 + 3 a + 2 với a ≠ ± 2 và a ≠ − 1 .
Không dùng các phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là
Cho đa thức A = 2 x 3 + x 2 − 13 x + 6 và hai phân thức: x 2 x 2 + 5 x − 3 , x + 2 x 2 + x − 6 với x ≠ − 3 ; x ≠ 1 2 và x ≠ 2 .
a) Chia đa thức A lần lượt cho các mẫu thức của hai phân thức đã cho.
b) Quy đồng mẫu thức của hai phân thức đã cho.
Cho hai phân thức 1 x 2 + ax − 2 và 2 x 2 + 4 x − b , với x ≠ − 3 ; x ≠ − 1 và x ≠ 2 .
a) Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là A = x 3 + 2 x 2 − 5 x − 6 ;
b) Với a và b tìm được hãy viết hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là A = x 3 + 2 x 2 − 5 x − 6 .
Cho các phân thức x − 3 2 x 2 − 3 x − 2 và 2 x − 1 x 2 + x − 6 với x ≠ − 3 ; x ≠ − 1 2 và x ≠ 2 . Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là N = 2 x 3 + 3 x 2 − 11 x − 6 .
Cho hai phân thức 1 x 2 + a x - 2 và 2 x 2 + 5 x + b . Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là x 3 + 4 x 2 + x - 6 . Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là x 3 + 4 x 2 + x - 6