Giải phương trình sau :
\(\sin^2x-\cos^2x=\cos4x\)
CMR
( tanx-1)/cos4x = (sin 2x-cos 2x)/(sin 2x+cos 2x)
Lời giải:
Bạn xem lại đề. 2 vế không bằng nhau. Ta có:
\(\frac{\sin 2x-\cos 2x}{\sin 2x+\cos 2x}=\frac{(\sin 2x-\cos 2x)(\cos 2x-\sin 2x)}{(\sin 2x+\cos 2x)(\cos 2x-\sin 2x)}=\frac{-(\sin 2x-\cos 2x)^2}{\cos ^22x-\sin ^22x}=\frac{-(\sin ^22x+\cos ^22x-2\sin 2x\cos 2x)}{\cos 4x}\)
\(=\frac{-(1-\sin 4x)}{\cos 4x}=\frac{\sin 4x-1}{\cos 4x}\)
Giải các phương trình sau :
a) \(\cos^2x+2\sin x\cos x+5\sin^2x=2\)
b) \(3\cos^2x-2\sin2x+\sin^2x=1\)
c) \(4\cos^2x-3\sin x\cos x+3\sin^2x=1\)
Giải phương trình sau :
\(2\sin^2x+\sin x\cos x-\cos^2x=3\)
Đây là dạng phương trình thuần nhất bậc 2 đối với sin và cos
Cách giải : Xét 2 trường hợp
TH1 : cos x = 0 => 2\(\sin^2x\)= 3 ( không thỏa mãn )=> pt vô nghiệm
TH2 : cos x \(\ne\)0 . Chia cả 2 vế cho \(\cos^2x\)ta được
\(2\tan^2x+\tan x-1=3\times\left(1+\tan^2x\right)\)
Giải phương trình tìm ra nghiệm và kết luận
Giải các phương trình sau :
a) \(2\sin^2x+\sin x\cos x-3\cos^2x=0\)
b) \(3\sin^2-4\sin x\cos x+5\cos^2x=2\)
c) \(\sin^2x+\sin2x-2\cos^2+5\cos^2x=2\)
d) \(2\cos^2x-3\sqrt{3}\sin2x-4\sin^2x=-4\)
a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Vậy ![]()
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan3 + kπ, k ∈ Z.
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; ![]() =
= ![]() (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
(sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
![]() sin2x + 2sinxcosx -
sin2x + 2sinxcosx - ![]() cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan(-5) + kπ, k ∈ Z.
+ kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 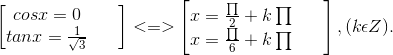
dùng công thức hạ bậc để giải các phương trình sau :
a) \(\sin^24x+\sin^23x=\sin^22x+\sin^2x\)
b) \(\cos^2x+\cos^22x+\cos^23x+\cos^24x=2\)
a)\(pt\Leftrightarrow\frac{1-cos8x}{2}+\frac{1-cos6x}{2}=\frac{1-cos4x}{2}+\frac{1-cos2x}{2}\)
\(\Leftrightarrow cos2x+cos4x=cos6x+cos8x\)
\(\Leftrightarrow2cos3x\cdot cosx=2cos7x\cdot cosx\)
\(\Leftrightarrow2cos\left(cos3x-cos7x\right)=0\)
\(\Leftrightarrow2cosx\cdot\left(-2\right)\cdot sin5x\cdot sin\left(-2x\right)=0\)
\(\Leftrightarrow cosx\cdot sin2x\cdot sin5x=0\)
\(\Leftrightarrow sin2x\cdot sin5x=0\)(do sin2x=0 <=>2sinx*cosx=0 gồm th cosx=0 r`)
\(\Leftrightarrow\left[\begin{array}{nghiempt}sin2x=0\\sin5x=0\end{array}\right.\)\(\Rightarrow\left[\begin{array}{nghiempt}x=\frac{k\pi}{2}\\x=\frac{k\pi}{5}\end{array}\right.\)\(\left(k\in Z\right)\)
b)\(pt\Leftrightarrow1-cos2x+1-cos4x=1+cos6x+1+cos8x\)
\(\Leftrightarrow cos2x+cos8x+cos4x+cos6x=0\)
\(\Leftrightarrow cos10x\cdot cos6x+cos10x\cdot cos2x=0\)
\(\Leftrightarrow cos10x\left(cos6x+cos2x\right)=0\)
\(\Leftrightarrow cos10x\cdot cos8x\cdot cos4x=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}cos10x=0\\cos8x=0\\cos4x=0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=\frac{\pi}{20}+\frac{k\pi}{10}\\x=\frac{\pi}{16}+\frac{k\pi}{8}\\x=\frac{\pi}{8}+\frac{k\pi}{4}\end{array}\right.\)
\(cos^2x-sin2x-sin^2x=1\)
\(\Leftrightarrow1-sin^2x-2sinx.cosx-sin^2x=1\)
\(\Leftrightarrow sin^2x+sinx.cosx=0\)
\(\Leftrightarrow sinx\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\tanx=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
Giải các phương trình sau
1) \(\sin^6x+\cos^6x=\cos4x\)
2) \(\sin^2\left(2x+\frac{5\pi}{12}\right)+\sin^2\left(x+\frac{\pi}{12}\right)=1\)
3) \(\sin x.\cos4x-\sin^22x=4\sin^2\left(\frac{\pi}{4}-\frac{x}{2}\right)-\frac{7}{2}\)
bài 1 bung công thức sin^6(x) + cos^6(x) là 5/8 + 3/8cos4x = cos4x chuyển vế giải
bài 2 dùng công thức hạ bậc sau đó dùng công thức cộng là ra
Giải phương trình sau:
a) $\tan ^2x+4\cos ^2x+7=4\tan x+8\cot x$
b) $6\sin ^2x+2\cos ^2x-2\sqrt{3}\sin 2x=14\sin \left(x-\frac{\pi }{6}\right)$
Giải phương trình lượng giác sau :
cos 2x - 3 sin x = 2