giải phương trình và bất phương trình
/x-5/=2x
giải phương trình và bất phương trình
/x-5/=2x
(x-2)^2+2(x-1)<=x^2+4
\(\left|x-5\right|=2x\)ĐK : x>=0
TH1 : x - 5 = 2x <=> x = -5 ( loại )
TH2 : x - 5 = -2x <=> 3x = 5 <=> x = 5/3 ( tm )
Vậy tập nghiệm pt là S = { 5/3 }
\(\left(x-2\right)^2+2\left(x-1\right)\le x^2+4\)
\(\Leftrightarrow x^2-4x+4+2x-2-x^2-4\le0\)
\(\Leftrightarrow-2x-2\le0\Leftrightarrow x+1\ge0\Leftrightarrow x\ge-1\)
Vậy tập nghiệm bft là S = { x | x > = -1 }
Ta có: \(\left|x-5\right|=2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=2x\left(x\ge5\right)\\x-5=-2x\left(x< 5\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2x=5\\x+2x=5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=5\\3x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\left(loại\right)\\x=\dfrac{5}{3}\left(nhận\right)\end{matrix}\right.\)
Bài 3 :Cho bất phương trình : 3x(2x + 5) x(6x -1) + 4
a) Giải bất phương trình và biểu diễn tập nghiệm trên trục số.
b) Tìm nghiệm nguyên nhỏnhất của bất phương trình trên.
giải các bất phương trình tích và các bất phương trình thương
b/ \(\dfrac{3x+5}{2x^2-5x+3}\)≥0
c/2x3+x+3>0
Lời giải:
b/
\(\frac{3x+5}{2x^2-5x+3}\geq 0\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} 3x+5\geq 0\\ 2x^2-5x+3>0\end{matrix}\right.\\ \left\{\begin{matrix} 3x+5\leq 0\\ 2x^2-5x+3<0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x\geq \frac{-5}{3}\\ x>\frac{3}{2}(\text{hoặc}) x< 1\end{matrix}\right.\\ \left\{\begin{matrix} x\leq \frac{-5}{3}\\ 1< x< \frac{3}{2}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow \left[\begin{matrix} x>\frac{3}{2}\\ \frac{-5}{3}\leq x< 1\end{matrix}\right.\ \)
c/
$2x^3+x+3>0$
$\Leftrightarrow 2x^2(x+1)-2x(x+1)+3(x+1)>0$
$\Leftrightarrow (x+1)(2x^2-2x+3)>0$
$\Leftrightarrow (x+1)[x^2+(x-1)^2+2]>0$
$\Leftrightarrow x+1>0$
$\Leftrightarrow x>-1$
Bài 1: Giải các bất phương trình và phương trình sau :
a) 2(3-4x) = 10-(2x – 5)
Giải các bất phương trình và phương trình sau :
a) 3(2-4x) = 11-(3x – 1)
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
Giải phương trình và bất phương trình:
a ) 9 x 2 - 4 = x - 1 x + 2 + 3 x - 2 b ) x - 5 = 2 x c ) x - 2 2 + 2 x - 1 ≤ x 2 + 4
a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
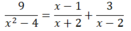
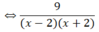
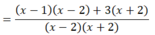
![]()
![]()
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}
Giải phương trình và bất phương trình
a) \(3\sqrt{-x^2+x+6}+2\left(2x-1\right)>0\)
b)\(\sqrt{2x^2+8x+5}+\sqrt{2x^2-4x+5}=6\sqrt{x}\)
a.
\(3\sqrt{-x^2+x+6}\ge2\left(1-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-x^2+x+6\ge0\\1-2x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}1-2x\ge0\\9\left(-x^2+x+6\right)\ge4\left(1-2x\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\le x\le3\\x>\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\25\left(x^2-x-2\right)\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}< x\le3\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\-1\le x\le2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow-1\le x\le3\)
b.
ĐKXĐ: \(x\ge0\)
\(\Leftrightarrow\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0\)
\(\Leftrightarrow\dfrac{2x^2+8x+5-16x}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-4x+5-4x}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)
\(\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)
\(\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0\)
\(\Leftrightarrow2x^2-8x+5=0\)
\(\Leftrightarrow x=\dfrac{4\pm\sqrt{6}}{2}\)
Câu b còn 1 cách giải nữa:
Với \(x=0\) không phải nghiệm
Với \(x>0\) , chia 2 vế cho \(\sqrt{x}\) ta được:
\(\sqrt{2x+8+\dfrac{5}{x}}+\sqrt{2x-4+\dfrac{5}{x}}=6\)
Đặt \(\sqrt{2x-4+\dfrac{5}{x}}=t>0\Leftrightarrow2x+8+\dfrac{5}{x}=t^2+12\)
Phương trình trở thành:
\(\sqrt{t^2+12}+t=6\)
\(\Leftrightarrow\sqrt{t^2+12}=6-t\)
\(\Leftrightarrow\left\{{}\begin{matrix}6-t\ge0\\t^2+12=\left(6-t\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t\le6\\12t=24\end{matrix}\right.\)
\(\Rightarrow t=2\)
\(\Rightarrow\sqrt{2x-4+\dfrac{5}{x}}=2\)
\(\Leftrightarrow2x-4+\dfrac{5}{x}=4\)
\(\Rightarrow2x^2-8x+5=0\)
\(\Leftrightarrow...\)
Bài 1.*) Giải phương trình
a) 1 + 5x = 2x + 7 b) 3 – 5(x+3) = x + 1 c)![]()
**) Giải bất phương trình và biểu diễn tập nghiệm trên trục số
a) 4x + 5 > 2x – 2 b) 2 (x - 2) < 5x + 2 (mũi tên kia thêm gạch ngang câub) giúp mình nha :))
Tìm sai lầm trong các "lời giải" sau:
a) Giải bất phương trình -2x > 23. Ta có:
-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.
Vậy nghiệm của bất phương trình là x > 25.
b) Giải bất phương trình 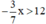 . Ta có:
. Ta có:
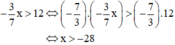
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với 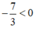 mà không đổi chiều bất phương trình.
mà không đổi chiều bất phương trình.
Lời giải đúng:
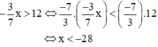
Vậy nghiệm của bất phương trình là x < -28
giải bất phương trình 2x-3/x-1<1/3
giải bất phương trình 2x-3/x-1 > 1/3
\(\dfrac{2x-3}{x-1}< \dfrac{1}{3}\left(đk:x\ne1\right)\)
\(\Leftrightarrow6x-9< x-1\Leftrightarrow5x< 8\Leftrightarrow x< \dfrac{8}{5}\) và ĐK \(x\ne1\)
\(\dfrac{2x-3}{x-1}>\dfrac{1}{3}\left(đk:x\ne1\right)\)
\(\Leftrightarrow x-1< 6x-9\Leftrightarrow5x>8\Leftrightarrow x>\dfrac{8}{5}\) và ĐK \(x\ne1\)