Bài 4: Bất phương trình bậc nhất một ẩn.

4x+7>23

<=> 4x>16

<=>x> 4

Vậy tập nghiệm của bpt là{ x/x>4}

//////////////////|-----------)----------------->

                 0             4

\(11x-20< 4+5x\\ \Leftrightarrow11x-5x< 4+20\\ \Leftrightarrow6x< 24\\ \Leftrightarrow x< 24:6\\ \Leftrightarrow x< 4\)

=>x^2+x-2-x-3+5<0

=>x^2<0

=>\(x\in\varnothing\)

Đề không đầy đủ. Bạn xem lại.

Khi m=1 thì (*) sẽ là 10x=2

=>x=1/5

Khi m=-1 thì (*) sẽ là 10x=0

=>x=0

Khi m=2 thì (*) sẽ là 10x-3=0

=>x=3/10

Khi m=-2 thì (*) sẽ là 10x=-1

=>x=-1/10

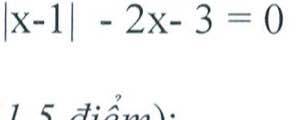
\(\left|x-1\right|-2x-3=0\)

\(\Leftrightarrow\left|x-1\right|=3+2x\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=3+2x\\x-1=-\left(3+2x\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2x=3+1\\x-1=-3-2x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}-x=4\\x+2x=-3+1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\3x=-2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)

|x-1|-2x-3=0

=>|x-1|=2x+3

TH1:x-1=2x+3

        x-2x=1+3

        -x=4

         x=-4

TH2:-x+1=2x+3

         -x-2x=-1+3

          -3x=2

              x=-2/3

Vậy S={-2/3}

=>x>=-1 và (3x-5)^2=(x+1)^2

=>x>=-1 và (3x-5-x-1)(3x-5+x+1)=0

=>x>=-1 và (4x-4)(2x-6)=0

=>x=1 hoặc x=3

BĐT chỉ đúng trong trường hợp a;b;c dương.

Với mọi số thực dương x;y ta có:

\(\left(x-y\right)^2\ge0\Leftrightarrow x^2+y^2\ge2xy\)

\(\Leftrightarrow\left(x+y\right)^2\ge4xy\Leftrightarrow\dfrac{x+y}{xy}\ge\dfrac{4}{x+y}\)

\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\)

Áp dụng:

\(\dfrac{1}{a+b}+\dfrac{1}{b+c}\ge\dfrac{4}{a+b+b+c}=\dfrac{4}{a+2b+c}\)

\(\dfrac{1}{a+b}+\dfrac{1}{a+c}\ge\dfrac{4}{2a+b+c}\)

\(\dfrac{1}{b+c}+\dfrac{1}{c+a}\ge\dfrac{4}{a+b+2c}\)

Cộng vế và rút gọn:

\(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\ge\dfrac{2}{a+2b+c}+\dfrac{2}{a+b+2c}+\dfrac{2}{2a+b+c}\)

Dấu "=" xảy ra khi \(a=b=c\)

\(\dfrac{M}{N}=\dfrac{x^3-4x^2-3x+18}{x^3-2x^2-15x+36}\)

\(=\dfrac{x^3-3x^2-x^2+3x-6x+18}{x^3-3x^2+x^2-3x-12x+36}\)

\(=\dfrac{\left(x-3\right)\left(x^2-x-6\right)}{\left(x-3\right)\left(x^2+x-12\right)}=\dfrac{\left(x-3\right)\left(x+2\right)}{\left(x+4\right)\left(x-3\right)}=\dfrac{x+2}{x+4}\)

Để P nguyên thì x+4-2 chia hết cho x+4

=>\(x+4\in\left\{1;-1;2;-2\right\}\)

=>\(x\in\left\{-3;-5;-2;-6\right\}\)

=>a=-2; b=-6

=>a*b=12