Tìm m để phương trình (m + 1)\(x^2\) - 2mx + m + 6 = 0 có hai nghiệm phân biệt x1 và x2 thỏa mãn 0 < x1 <x2
§5. Dấu của tam thức bậc hai
\(\Leftrightarrow\left\{{}\begin{matrix}m+1\ne0\\\Delta'=m^2-\left(m+1\right)\left(m+6\right)>0\\x_1+x_2=\dfrac{2m}{m+1}>0\\x_1x_2=\dfrac{m+6}{m+1}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\-7m-6>0\\\dfrac{2m}{m+1}>0\\\dfrac{m+6}{m+1}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -\dfrac{6}{7}\\\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\\\left[{}\begin{matrix}m>-1\\m< -6\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m< -6\)
Đúng 2
Bình luận (0)
Tìm m để :
1) (m + 1)\(x^2\) - 2(m + 1)x + 3m - 3 < 0 có nghiệm
2) \(x^2\) + 2(m + 2)x - 2m - 1 > 0 có nghiệm
3) (m-1)\(x^2\) - 2(m + 1)x + 3m - 6 ≤ 0 có nghiệm
a.
- Với \(m=-1\) BPT có nghiệm (đúng với mọi x)
- Với \(m\ne-1\) BPT có nghiệm khi:
\(\left[{}\begin{matrix}m+1< 0\\\left\{{}\begin{matrix}m+1>0\\\Delta'=\left(m+1\right)^2-\left(m+1\right)\left(3m-3\right)>0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\\left\{{}\begin{matrix}m>-1\\\left(m+1\right)\left(4-2m\right)>0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\\left\{{}\begin{matrix}m>-1\\-1< m< 2\end{matrix}\right.\end{matrix}\right.\)
Kết hợp lại ta được: \(m< 2\)
b.
Do \(a=1>0\) nên BPT có nghiệm với mọi m
c.
- Với \(m=1\) BPT có nghiệm
- Với \(m\ne1\) BPT có nghiệm khi:
\(\left[{}\begin{matrix}m-1< 0\\\left\{{}\begin{matrix}m-1>0\\\Delta'=\left(m+1\right)^2-\left(m-1\right)\left(3m-6\right)\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< 1\\\left\{{}\begin{matrix}m>1\\-2m^2+11m-5\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< 1\\\left\{{}\begin{matrix}m>1\\\dfrac{1}{2}\le m\le5\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m< 1\\1< m\le5\end{matrix}\right.\)
Kết hợp lại ta được: \(m\le5\)
Đúng 2
Bình luận (0)
Tìm m để:
(\(m^2\) - 3m - 4)\(x^2\) - 2(m - 4)x + 3 < 0 vô nghiệm
Đặt: \(f\left(x\right)=\left(m^2-3m-4\right)x^2-2\left(m-4\right)x+3\).
Khi \(\left[{}\begin{matrix}m=-1\\m=4\end{matrix}\right.\) thì \(\left[{}\begin{matrix}f\left(x\right)=10x+3\\f\left(x\right)=-12x+3\end{matrix}\right.\). Dễ thấy \(f\left(x\right)< 0\) luôn có nghiệm.
Khi \(m\notin\left\{-1;4\right\}\)
Để \(f\left(x\right)< 0\) vô nghiệm thì \(f\left(x\right)\ge0\forall x\in R\)
Khi đó: \(\left\{{}\begin{matrix}m^2-3m-4\ge0\\\Delta'=\left[-\left(m-4\right)\right]^2-\left(m^2-3m-4\right)\cdot3< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\le-1\\m\ge4\end{matrix}\right.\\-2m^2+m+28< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\le-1\\m\ge4\end{matrix}\right.\\\left[{}\begin{matrix}m< -\dfrac{7}{2}\\m>4\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}m< -\dfrac{7}{2}\\m>4\end{matrix}\right.\)
Vậy: \(f\left(x\right)< 0\) vô nghiệm khi \(m\in\left(-\infty;-\dfrac{7}{2}\right)\cup\left(4;+\infty\right)\)
Đúng 3
Bình luận (0)
Tìm m để :
(m + 2)\(x^2\) - 2(m + 2)x + 3m + 4 < 0, ∀x∈R
+) \(m+2=0\Leftrightarrow m=-2\Rightarrow-2< 0\left(TM\right)\)
+) \(m+2\ne0\Leftrightarrow m\ne-2\)
\(\left(m+2\right)x^2-2\left(m+2\right)x+3m+4< 0,\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+2< 0\\\Delta'< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\\left(m+2\right)^2-\left(m+2\right)\left(3m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\-2m^2-6m-4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m\in\left(-\infty;-2\right)\cup\left(-1;+\infty\right)\end{matrix}\right.\)
\(\Rightarrow m\in\left(-\infty;-2\right)\)
Vậy \(m\in(-\infty;-2]\)
Đúng 1
Bình luận (2)
Tìm m để BPT:
\(\dfrac{-x^2+2x-5}{x^2-mx+1}\) ≤ 0, đúng ∀x∈R
Do \(-x^2+2x-5=-\left(x-1\right)^2-4< 0;\forall x\in R\)
Nên BPT tương đương:
\(\dfrac{1}{x^2-mx+1}\ge0\) ; \(\forall x\)
\(\Leftrightarrow x^2-mx+1>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta=m^2-4< 0\end{matrix}\right.\)
\(\Rightarrow-2< m< 2\)
Đúng 2
Bình luận (0)
Tìm m để:
f(x)= (m+1)\(x^2\) +5x + 2 > 0, ∀x∈R
< 0, ∀x∈R
≥ 0, ∀x∈R
≤ 0, ∀x∈R
1. Khi \(m=-1\Rightarrow5x+2>0\Rightarrow x>-\dfrac{2}{5}\), suy ra \(f\left(x\right)>0\) không có tập nghiệm là \(R\).
Khi \(m\ne-1,f\left(x\right)>0\forall x\in R\) khi:
\(\left\{{}\begin{matrix}m+1>0\\\Delta=5^2-4\cdot2\left(m+1\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\m>\dfrac{17}{8}\end{matrix}\right.\)
Vậy: \(m>\dfrac{17}{8}\)
2. Cũng chia ra hai trường hợp khi \(m=-1,m\ne-1\) như trên.
Khi \(m\ne-1,f\left(x\right)< 0\forall x\in R\) khi:
\(\left\{{}\begin{matrix}m+1< 0\\\Delta=5^2-4\cdot2\left(m+1\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -1\\m>\dfrac{17}{8}\end{matrix}\right.\) (vô lí)
Vậy: \(m\in\varnothing\)
3, 4. Làm tương tự như hai ý 1, 2 nhé.
Đúng 2
Bình luận (0)
TH1: m=-1
\(\Leftrightarrow f\left(x\right)=\left(-1+1\right)x^2+5x+2\)
=>f(x)=5x+2
=>Khi m=-1 thì f(x)>0 khi x>-2/5; f(x)>=0 khi x>=-2/5; f(x)<0 khi x<-2/5; f(x)<=0 khi x<=-2/5
=>Loại
TH2: \(m\ne-1\)
\(f\left(x\right)=\left(m+1\right)x^2+5x+2\)
\(\text{Δ}=5^2-4\cdot\left(m+1\right)\cdot2\)
\(=25-8m-8=-8m+17\)
Để f(x)>=0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m+17< =0\\m+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m< =-17\\m>-1\end{matrix}\right.\Leftrightarrow m>=\dfrac{17}{8}\)
Để f(x)<=0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m+17< =0\\m+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>=\dfrac{17}{8}\\m< -1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Để f(x)>0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m+17< 0\\m+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>\dfrac{17}{8}\\m>-1\end{matrix}\right.\Leftrightarrow m>\dfrac{17}{8}\)
Để f(x)<0 với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-8m+17< 0\\m+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>\dfrac{17}{8}\\m< -1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Đúng 1
Bình luận (0)
Tìm m để :
f(x)= (\(m^2\)+2)\(x^2\) - 2(m-1)x + 1 > 0, ∀x∈R
\(f\left(x\right)>0\forall x\in R\)
\(\Rightarrow\left\{{}\begin{matrix}m^2+2>0\left(LĐ\right)\\\Delta'=\left[-\left(m-1\right)\right]^2-\left(m^2+2\right)\cdot1< 0\end{matrix}\right.\)
\(\Rightarrow m^2-2m+1-m^2-2< 0\)
\(\Leftrightarrow m>-\dfrac{1}{2}\)
Vậy: \(m>-\dfrac{1}{2}\).
Đúng 1
Bình luận (0)
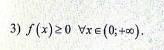
f(x)= x^2-2mx-m+90
Bạn nên viết lại đề cho rõ ràng để mọi người hỗ trợ tốt hơn.
Đúng 0
Bình luận (0)
mọi người giúp em bài 4 với ạ
4:
a: Δ=(2m+4)^2-4*2*(3m+2)
=4m^2+16m+16-24m-16
=4m^2-8m
Để f(x)>0 với mọi x thì 4m^2-8m<0
=>0<m<2
b: Δ=m^2-4*(-3)*m=m^2+12m
f(x)<0 với mọi x thì m^2+12m<0
=>-12<m<0
Đúng 0
Bình luận (0)
Tất cả các giá trị của tham số m để hàm số f(x) =1/ (\/2x*2-3x+3m-2) có tập xác định D=R
Để hàm số có TXĐ là D=R thì 2x^2-3x+3m-2>0
\(\Delta=\left(-3\right)^2-4\cdot2\cdot\left(3m-2\right)\)
=9-8(3m-2)
=9-24m+16
=-24m+25
Để BPT luôn có nghiệm thì -24m+25<0 và 2>0
=>-24m<-25
=>m>25/24
Đúng 0
Bình luận (0)



