Đơn giản biểu thức ;
\(\left(1+\tan^2\alpha\right)\cos^2\alpha+\left(1+\cot^2\alpha\right)\sin^2\alpha\)
Đơn giản các biểu thức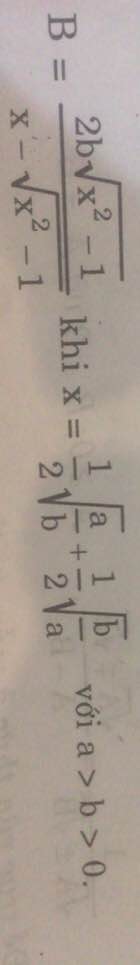
Lần sau đăng đề bạn nên gõ công thức cho gọn, đừng đăng ảnh dài oạch như thế này nhìn rất khó.
Lời giải:
Ta có:
\(x^2=\frac{1}{4}(\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}})^2=\frac{1}{4}(\frac{a}{b}+\frac{b}{a}+2)\)
\(\Rightarrow x^2-1=\frac{1}{4}(\frac{a}{b}+\frac{b}{a}-2)=\frac{1}{4}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})^2\)
\(\Rightarrow \sqrt{x^2-1}=\frac{1}{2}|\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}|=\frac{1}{2}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})\)
Do đó:
\(2b\sqrt{x^2-1}=b.\frac{a-b}{\sqrt{ab}}=(a-b).\sqrt{\frac{b}{a}}\)
\(x-\sqrt{x^2-1}=\frac{1}{2}[\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}-(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})]\)
\(=\sqrt{\frac{b}{a}}\)
$\Rightarrow B=a-b$

Đơn giản biểu thức trên
`S=[cos(a+\pi/3)+cos(a-\pi/3)]/[cot a-cot (a/2)]`
`S=[2.cos a.cos(\pi/3)]/[[cos a]/[sin a]-[cos (a/2)]/[sin (a/2)]]`
`S=[2 .cos a. 1/2]/[[cos a.sin a/2 -sin a.cos (a/2)]/[sin a.sin (a/2)]`
`S=[cos a.sin a.sin (a/2)]/[1/2[sin(3/2 a)+sin (-1/2a)-sin (3/2 a)-sin (1/2a)]]`
`S=[2.cos a.sin a.sin (a/2)]/[sin (-1/2 a)-sin(1/2 a)]`
`S=[sin 2a.sin(a/2)]/[-sin(1/2a)-sin (1/2a)]`
`S=-1/2 sin 2a`.
Đơn giản các biểu thức sau ( giả sử các biểu thức sau đều có nghĩa )
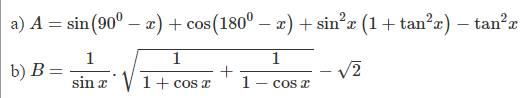
a) \(A=sin\left(90^0-x\right)+cos\left(180^0-x\right)+sin^2x\left(1+tan^2x\right)-tan^2x\)
\(=cosx-cosx+sin^2x.\left(\dfrac{1}{cos^2x}\right)-tan^2x\)
\(=tan^2x-tan^2x\)
\(=0\)
b) \(B=\dfrac{1}{sinx}.\sqrt{\dfrac{1}{1+cosx}+\dfrac{1}{1-cosx}}-\sqrt{2}\)
\(=\dfrac{1}{sinx}.\sqrt{\dfrac{1-cosx+1+cosx}{1-cos^2x}}-\sqrt{2}\)
\(=\dfrac{1}{sinx}.\sqrt{\dfrac{2}{sin^2x}}-\sqrt{2}\)
\(=\dfrac{\sqrt{2}}{sin^2x}-\sqrt{2}\)
\(=\dfrac{\sqrt{2}\left(1-sin^2x\right)}{sin^2x}\)
\(=\dfrac{\sqrt{2}cos^2x}{sin^2x}\)
\(=\sqrt{2}tan^2x\)
1) Đơn giản biểu thức : \(P=\frac{1-sin^2x.cos^2x}{cos^2x}-cos^2x\)
2)Đơn giản biểu thức : \(M=\frac{2cos^2x-1}{sinx+cosx}\)
\(P=\frac{1-sin^2x.cos^2x}{cos^2x}-cos^2x=\frac{1}{cos^2x}-sin^2x-cos^2x\)
\(=1+tan^2x-\left(sin^2x+cos^2x\right)=1+tan^2x-1=tan^2x\)
\(M=\frac{2cos^2x-1}{sinx+cosx}=\frac{2cos^2x-\left(sin^2x+cos^2x\right)}{sinx+cosx}=\frac{cos^2x-sin^2x}{sinx+cosx}\)
\(\frac{\left(cosx-sinx\right)\left(cosx+sinx\right)}{sinx+cosx}=cosx-sinx\)
Đơn giản biểu thức ![]() ta được:
ta được:
![]()
![]()
![]()
![]()
Đơn giản biểu thức ![]() , ta được:
, ta được:
A. x2( x + 1)
B. –x2(x + 1)
C. x2( x - 1)
D. x2|x + 1|
Đơn giản biểu thức 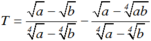 ta được:
ta được:
A. ![]()
B. ![]()
C. ![]()
D. a – b
Đơn giản biểu thức
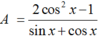
ta có
A. A = cosx + sinx.
B. A = cosx - sinx.
C. A = sinx - cosx.
D. A = -sinx - cosx.
Đơn giản biểu thức ![]() ta được:
ta được:
A . A = a2
B. A = a5/6
C. A = a2/3
D. A= a
Đơn giản biểu thức 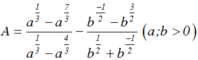 ta được:
ta được:
A. A = a + b
B. A = a - b
C. A = a + b + 2
D. A = a – b + 2
Chọn A.
Ta có:
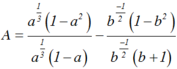
= 1 + a – (1 – b) = a + b