Cho cos a = 4/5 ; 0° < a < 90°. Tính giá trị của A = cos a +sin a / cos a - sin a
NT
Những câu hỏi liên quan
a) cho sin alpha = 4/5 tính a = 5 sin alpha + 3 cos alpha b) cho cotan alpha = 1/3 Tính B = sin alpha trừ cos alpha trên sin alpha + cos alpha bài này cho học sinh khá giỏi nè
Cho \(\tan\alpha-5\cot\alpha+4=0.\). Tính \(A=\frac{4\sin\alpha+2\cos\alpha}{3\sin\alpha-\cos\alpha}\)
\(tana-5cota+4=0\Rightarrow tana-\dfrac{5}{tana}+4=0\)
\(\Rightarrow tan^2a+4tana-5=0\Rightarrow\left[{}\begin{matrix}tana=1\\tana=-5\end{matrix}\right.\)
\(A=\dfrac{4sina+2cosa}{3sina-cosa}=\dfrac{\dfrac{4sina}{cosa}+\dfrac{2cosa}{cosa}}{\dfrac{3sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{4tana+2}{3tana-1}=\left[{}\begin{matrix}3\\\dfrac{9}{8}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Nếu \(\cos a = \frac{3}{5}\) và \(\cos b = - \frac{4}{5}\) thì \(\cos \left( {a + b} \right)\cos \left( {a - b} \right)\) bằng:
A.0
B.2
C.4
D.5
Ta có :
\(\cos \left( {a + b} \right)\cos \left( {a - b} \right) = \frac{1}{2}\left( {\cos 2a + \cos 2b} \right) = \frac{1}{2}\left( {2{{\cos }^2}a - 1 + 2{{\cos }^2}b - 1} \right) = 0\)
Chọn A
Đúng 0
Bình luận (0)
Cho sin a = 3/5 và cos a < 0 ; cos b = 3/4 và sin b > 0. Giá trị của sin(a - b) bằng :
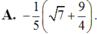
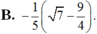
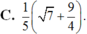
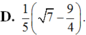
Chọn C.
Ta có :
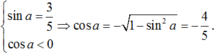
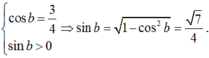
Áp dụng công thức cộng ta có:
sin(a – b) = sin a.cos b – cos a.sin b
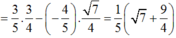
Đúng 0
Bình luận (0)
Cho sin x + cos x =5/4 . Tính giá trị của biểu thức : A = sin x . cos x , B = sin x - cos x
\(\left(sinx+cosx\right)^2=\frac{25}{16}\Rightarrow1+2sinx.cosx=\frac{25}{16}\)
\(\Rightarrow sinx.cosx=\frac{9}{32}\)
\(\left(sinx-cosx\right)^2=\left(sinx+cosx\right)^2-4sinx.cosx=\frac{25}{16}-4.\frac{9}{32}=\frac{7}{16}\)
\(\Rightarrow sinx-cosx=\pm\frac{\sqrt{7}}{4}\)
a, bt sin α=3/5, tính A= 5 \(sin^2\)α + 6\(cos^2\)α.
b,bt cos α= 4/5, tính B= 4\(sin^2\)α - 5\(cos^2\)α.
a) Ta có: \(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\cos^2\alpha=1-\dfrac{9}{25}=\dfrac{16}{25}\)
Ta có: \(A=5\cdot\sin^2\alpha+6\cdot\cos^2\alpha\)
\(=5\left(\sin^2\alpha+\cos^2\alpha\right)+\cos^2\alpha\)
\(=5+\dfrac{16}{25}=\dfrac{141}{25}\)
Đúng 0
Bình luận (1)
Cho sin a = 3/5 với π/2 < a < π Tính sin 2a , cos 2a , tan 2a , cot ( a - π/4 ) , sin a/2 , cos a/2 Cảm ơn trc❤
1) Cho \(\cos a.\sin a=\frac{1}{5}\)Tính cot a
2) Chứng minh rằng
a)\(\frac{\cos a}{1-\sin a}=\frac{1+\sin a}{\cos a}\)
b)\(\frac{\left(\sin a+\cos a\right)^2-\left(\sin a-\cos a\right)^2}{\sin a.\cos a}=4\)
\(cosa.sina=\frac{1}{5}\Rightarrow\frac{cosa.sina}{sin^2a}=\frac{1}{5sin^2a}=\frac{sin^2a+cos^2a}{5sin^2a}\)
\(\Rightarrow\frac{cosa}{sina}=\frac{1}{5}+\frac{1}{5}.\frac{cos^2a}{sin^2a}\)
\(\Rightarrow cota=\frac{1}{5}+\frac{1}{5}cot^2a\)
\(\Rightarrow cot^2a-5cota+1=0\)
\(\Rightarrow cota=\frac{5\pm\sqrt{21}}{2}\)
Đúng 0
Bình luận (0)
Câu 2:
\(\frac{cosa}{1-sina}=\frac{cosa\left(1+sina\right)}{\left(1-sina\right)\left(1+sina\right)}=\frac{cosa\left(1+sina\right)}{1-sin^2a}=\frac{cosa\left(1+sina\right)}{cos^2a}=\frac{1+sina}{cosa}\)
b/
\(\frac{\left(sina+cosa\right)^2-\left(sina-cosa\right)^2}{sina.cosa}\)
\(=\frac{sin^2a+cos^2a+2sina.cosa-\left(sin^2a+cos^2a-2sina.cosa\right)}{sina.cosa}\)
\(=\frac{4sina.cosa}{sina.cosa}\)
\(=4\)
Đúng 0
Bình luận (0)
Cho \(\sin a+\cos a=\frac{5}{4}\)
a, Tính \(\sin a\times\cos a\)
b, tính \(\sin a-\cos a\)
\(sina+cosa=\frac{5}{4}\Rightarrow\left(sina+cosa\right)^2=\frac{25}{16}\)
\(\Rightarrow sin^2a+cos^2a+2sina.cosa=\frac{25}{16}\)
\(\Rightarrow2sina.cosa=\frac{25}{16}-1=\frac{9}{16}\)
\(\Rightarrow sina.cosa=\frac{9}{32}\)
\(\Rightarrow1-\frac{9}{16}=sin^2a+cos^2a-2sina.cosa\)
\(\Leftrightarrow\left(sina-cosa\right)^2=\frac{7}{16}\)
\(\Rightarrow sina-cosa=\pm\frac{\sqrt{7}}{4}\)
Đúng 0
Bình luận (0)




