Bài 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180 ĐỘ

\(tan\alpha=3\)

\(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)

\(\Rightarrow cos\alpha=\pm\sqrt{\dfrac{1}{1+tan^2\alpha}}=\pm\sqrt{\dfrac{1}{1+3^2}}=\pm\dfrac{\sqrt{10}}{10}\)

\(\Rightarrow A\)

`tan a =3 <=> (sina)/(cosa) =3 <=> sina=3cosa`

Có: `sin^2a+cos^2a =1`

`<=> (3cosa)^2 + cos^2a =1`

`<=> 10cos^2a =1`

`<=> cosa = \pm \sqrt10/10`

`=>` A.

Bạn tham khảo

`sin^2x+cos^2x=1`

`<=>sin^2x+(1/2)^2=1`

`<=> sinx=\pm \sqrt3/2`

• `sinx=\sqrt3/2 => P=3. (\sqrt3/2)^2 +1=13/4`

• `sinx=-\sqrt3/2 => P = 3.(-\sqrt3/2) +1=13/4`

`=>` A.

\(P=3sin^2x+1=3\left(1-cos^2x\right)+1=3\left(1-\dfrac{1}{4}\right)+1=\dfrac{13}{4}\)

\(\pi< x< \dfrac{3\pi}{2}\Rightarrow\left\{{}\begin{matrix}sinx< 0\\cosx< 0\end{matrix}\right.\)

\(\Rightarrow sinx=-\sqrt{1-cos^2x}=-\dfrac{4}{5}\)

\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{4}{3}\) ; \(cotx=\dfrac{1}{tanx}=\dfrac{3}{4}\)

\(P=\dfrac{4}{3}+\dfrac{3}{4}=\dfrac{25}{12}\)

a, ( Chắc là tính AB :vvvv )

Ta có : \(m_a^2=4^2=\dfrac{AB^2+AC^2}{2}-\dfrac{BC^2}{4}\)

\(\Rightarrow AB=\sqrt{41}\)

 - Áp dụng công thức herong ta được : \(S_{ABC}=4\sqrt{5}\left(cm^2\right)\)

b, Ta có : \(S_{ABC}=\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.6.AH=4\sqrt{5}\)

\(\Rightarrow AH=\dfrac{4\sqrt{5}}{3}\left(cm\right)\)

- Áp dụng hệ quả định lý cos : \(CosACB=\dfrac{1}{9}\)

\(\Rightarrow\widehat{ACB}\approx83^o37^,\)

- Áp dụng định lý sin : \(\dfrac{BC}{SinA}=\dfrac{AB}{SinC}=\dfrac{AC}{SinB}\)

\(\Rightarrow\widehat{ABC}=28^O7^,\)

c, Ta có : \(S_{ABC}=4\sqrt{5}=\dfrac{abc}{4R}\)

\(\Rightarrow R=\dfrac{9\sqrt{205}}{40}\left(cm\right)\)

\(A=\dfrac{cos^2a-sin^2a}{\dfrac{cos^2a}{sin^2a}-\dfrac{sin^2a}{cos^2a}}-cos^2a=\dfrac{cos^2a.sin^2a\left(cos^2a-sin^2a\right)}{\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)}-cos^2a\)

\(=cos^2a.sin^2a-cos^2a=cos^2a\left(sin^2a-1\right)=-cos^4a\)

\(B=\sqrt{\left(1-cos^2a\right)^2+6cos^2a+3cos^4a}+\sqrt{\left(1-sin^2a\right)^2+6sin^2a+3sin^4a}\)

\(=\sqrt{4cos^4a+4cos^2a+1}+\sqrt{4sin^4a+4sin^2a+1}\)

\(=\sqrt{\left(2cos^2a+1\right)^2}+\sqrt{\left(2sin^2a+1\right)^2}\)

\(=2\left(sin^2a+cos^2a\right)+2=4\)

Giả sử trực tâm của tam giác ABC có tọa độ \(H\left(x;y\right)\)

\(\left\{{}\begin{matrix}\overrightarrow{BC}=\left(6;-2\right)\\\overrightarrow{AH}=\left(x-1;y\right)\end{matrix}\right.\Rightarrow\overrightarrow{BC}\perp\overrightarrow{AH}\Leftrightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)

\(\Leftrightarrow6\left(x-1\right)-2y=0\)

\(\Leftrightarrow3x-y=3\left(1\right)\) 

Lại có:

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;1\right)\\\overrightarrow{CH}=\left(x-5;y+1\right)\end{matrix}\right.\Rightarrow\overrightarrow{AB}\perp\overrightarrow{CH}\Leftrightarrow\overrightarrow{CH}.\overrightarrow{AB}=0\)

\(\Leftrightarrow-2\left(x-5\right)+y+1=0\)

\(\Leftrightarrow-2x+y=-11\left(2\right)\)

\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}x=-8\\y=-27\end{matrix}\right.\Rightarrow H\left(-8;-27\right)\)

Phương trình đường tròn (C) có dạng:

x² + y² -2ax – 2by + c= 0 ( a²+ b² –c > 0)

Do 3 điểm A; B; C thuộc (C) nên 

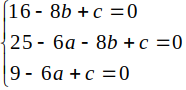
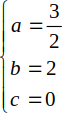
Vậy bán kính R= \(\sqrt{a^2+b^2-c^2}=\sqrt{\left(\dfrac{3}{2}\right)^2+2^2}=2.5\)

#TK

Suy ra diện tích tam giác ABC là 1/2.AB.BC = 6.