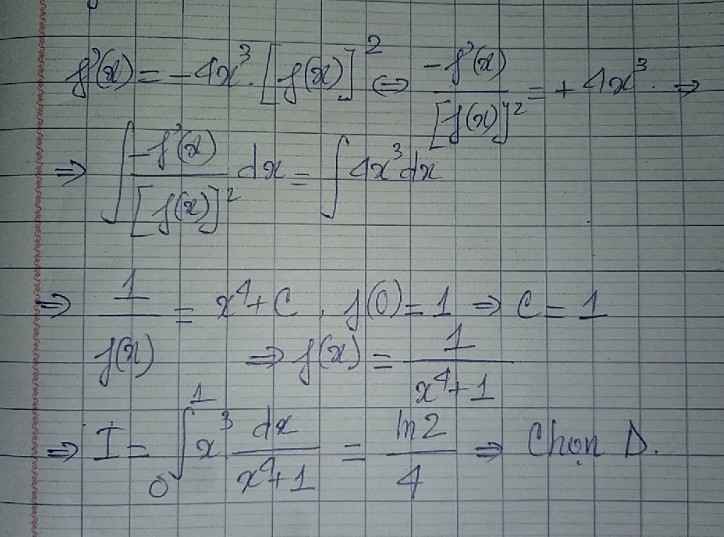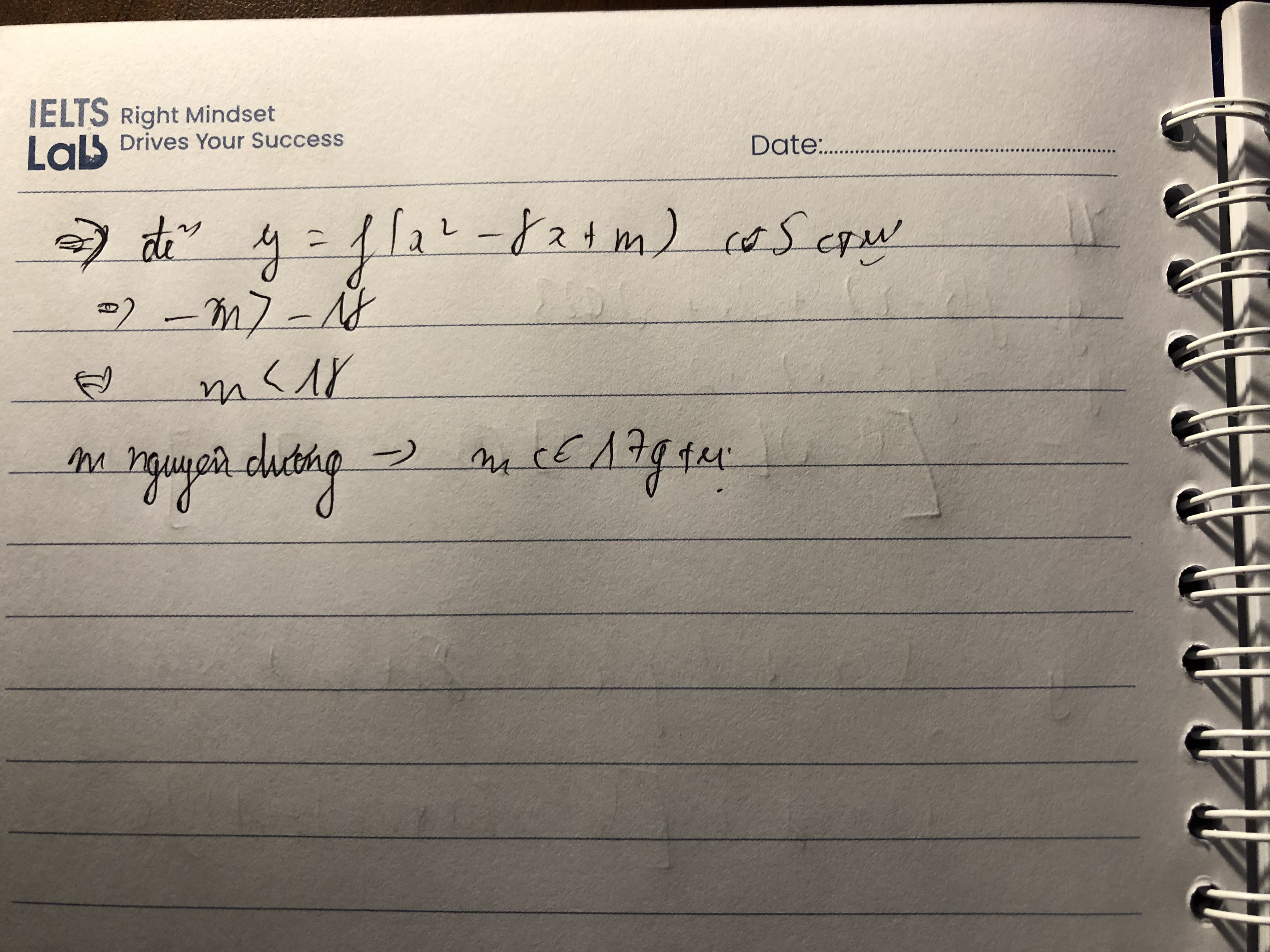Cho hàm số \(y=f\left(x\right)\) có đạo hàm và liên tục trên \(\left[0;\dfrac{\pi}{2}\right]\)thoả mãn \(f\left(x\right)=f'\left(x\right)-2cosx\). Biết \(f\left(\dfrac{\pi}{2}\right)=1\), tính giá trị \(f\left(\dfrac{\pi}{3}\right)\)
A. \(\dfrac{\sqrt{3}+1}{2}\) B. \(\dfrac{\sqrt{3}-1}{2}\) C. \(\dfrac{1-\sqrt{3}}{2}\) D. 0