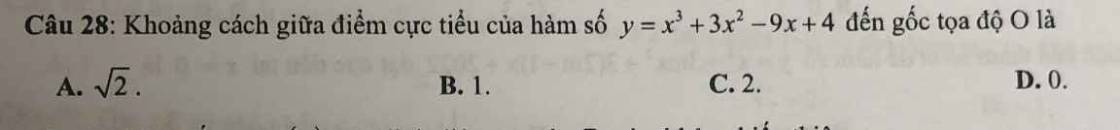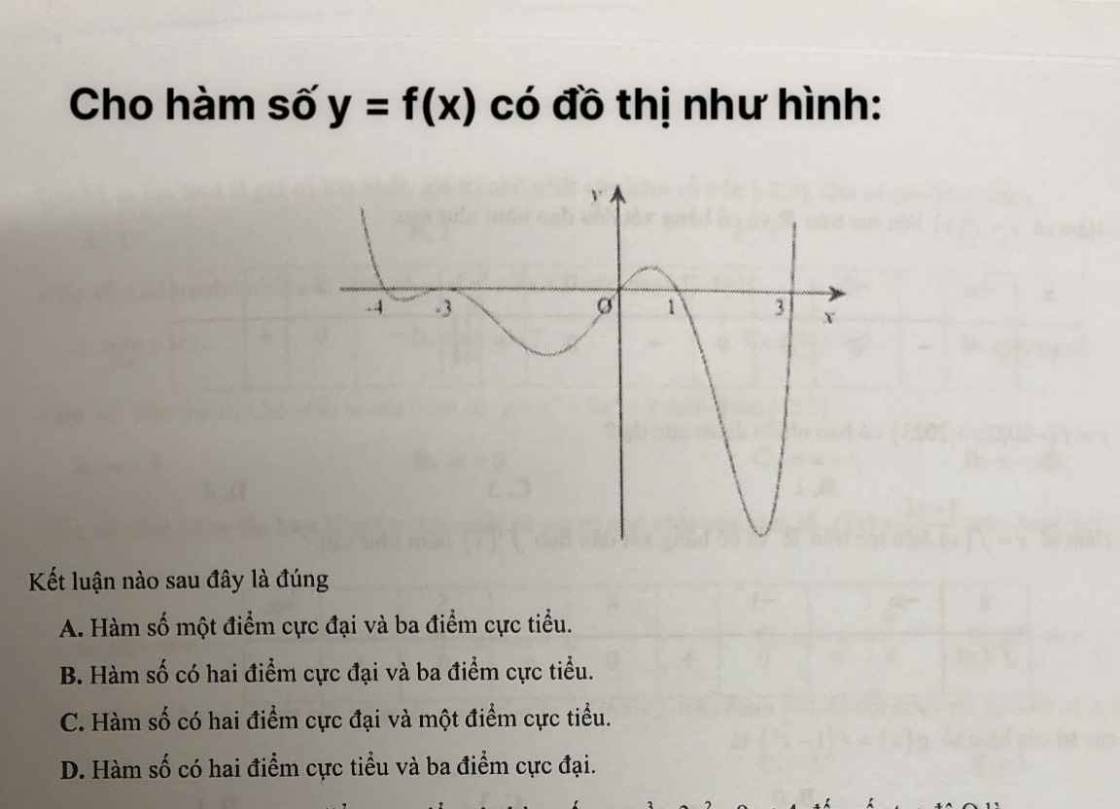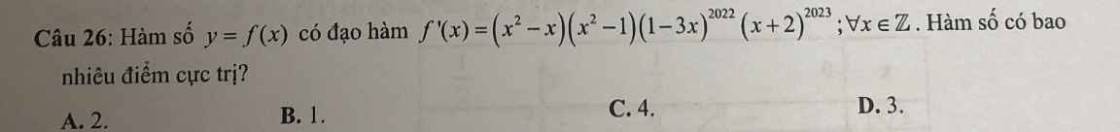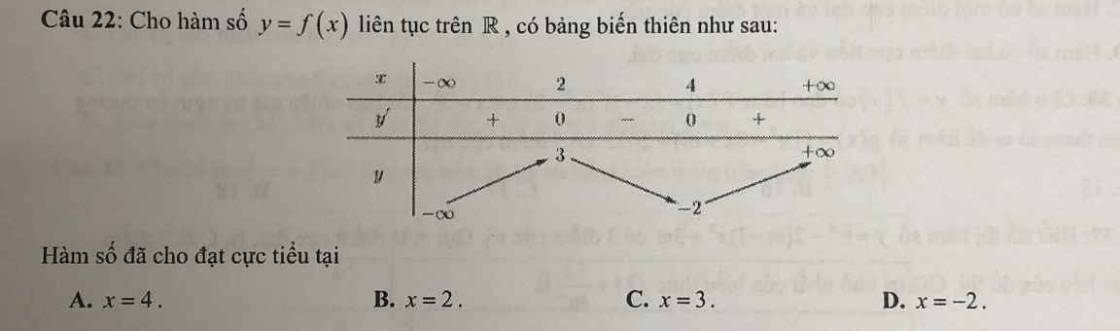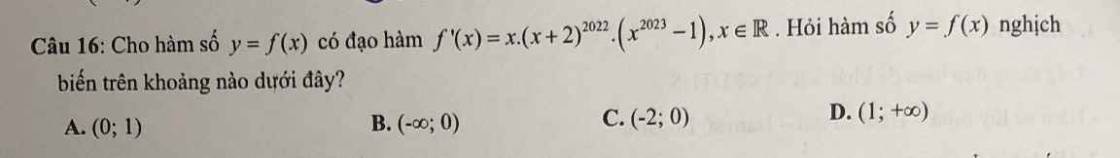
Bài 6: Ôn tập chương Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Chọn B

\(y=x^3+3x^2-9x+4\)

=>\(y'=3x^2+3\cdot2x-9=3x^2+6x-9\)

=>\(y''=3\cdot2x+6=6x+6\)

Đặt y'=0

=>\(3x^2+6x-9=0\)

=>\(x^2+2x-3=0\)

=>(x+3)(x-1)=0

=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)

Khi x=-3 thì \(y''=6\cdot\left(-3\right)+6=-18+6=-12< 0\)

=>x=-3 là cực đại của hàm số

Khi x=1 thì \(y''=6\cdot1+6=12>0\)

=>x=1 là cực tiểu của hàm số

Khi x=1 thì \(y=1^3+3\cdot1^2-9\cdot1+4=-1\)

=>A(1;-1) là cực tiểu của hàm số

\(AO=\sqrt{1^2+1^2}=\sqrt{2}\)

=>Chọn A

Chọn B

\(f'\left(x\right)=\left(x^2-x\right)\left(x^2-1\right)\left(1-3x\right)^{2022}\left(x+2\right)^{2023}\)

=>\(f'\left(x\right)=x\left(1-3x\right)^{2022}\left(x^2-1\right)\cdot\left(x+2\right)^{2022}\cdot\left(x-1\right)\left(x+2\right)\)

Chúng ta sẽ loại \(x;\left(1-3x\right)^{2022};\left(x^2-1\right);\left(x+2\right)^{2022}\) vì đây là những đa thức có bậc chẵn

=>Còn lại x-1;x+2

=>f(x) sẽ có 2 cực trị

=>Chọn A

TXĐ: D=R\{1/5}

\(y=\dfrac{4x+3}{5x-1}\)

\(y'=\dfrac{\left(4x+3\right)'\left(5x-1\right)-\left(4x+3\right)\left(5x-1\right)'}{\left(5x-1\right)^2}\)

\(\Leftrightarrow y'=\dfrac{4\left(5x-1\right)-5\left(4x+3\right)}{\left(5x-1\right)^2}\)

=>\(y'=\dfrac{20x-4-20x-15}{\left(5x-1\right)^2}=-\dfrac{19}{\left(5x-1\right)^2}\)<0 với mọi x thuộc TXĐ

=>Chọn C

Chọn C

Chọn A

Chọn A

Chọn B

Đặt f'(x)<0

=>\(x\left(x+2\right)^{2022}\left(x^{2023}-1\right)< 0\)

=>\(x\left(x^{2023}-1\right)< 0\)

TH1: \(\left\{{}\begin{matrix}x>0\\x^{2023}-1< 0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>0\\x< 1\end{matrix}\right.\)

=>0<x<1

TH2: \(\left\{{}\begin{matrix}x< 0\\x^{2023}-1>0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< 0\\x>1\end{matrix}\right.\)

=>Loại

Do đó: f'(x)<0 khi 0<x<1

=>Chọn A

Chọn C