Tìm các giá trị của m để hs y=X3+ (m -1)x2+xm-2 ngịch biến trên khoảng (1;3)
Bài 1: Sự đồng biến và nghịch biến của hàm số
Tam giác ABC vuông cân tại A nên AB/BC = 1/ V2 (V2 là căn bậc 2 của 2).
Tam tác PAB đồng dạng với Tam giác PBC vì PA/PB = PB/PC = AB/BC = 1/ V2 --> gócPAB = góc PBC.
GócPAB + gócPBA = gócPBC + góc PBA = góc ABC = 45 độ (do tam giác ABC vuông cân tại A).
Góc APB = 180 độ - (góc PAB + góc PBA) = 180 độ - 45 độ = 135 độ.
Đúng 0
Bình luận (0)
0,1a mol amin X tác dụng vừa đủ với 200 ml dung dịch HCl aM. Nhận định đúng về X là:A. X là amin no, don, hoB. X là amin 2 chức C. X có CT là C2H5NH2D. X là amin không no
Đọc tiếp
0,1a mol amin X tác dụng vừa đủ với 200 ml dung dịch HCl aM. Nhận định đúng về X là:
A. X là amin no, don, ho
B. X là amin 2 chức
C. X có CT là C2H5NH2
D. X là amin không no
Đây là bài hóa bạn cần cho vào box môn Hóa học nhé.
Đúng 0
Bình luận (0)
Xét tính đơn điệu của hàm số (có vẽ bảng biến thiên)
\(y = \sqrt{2x - x^3}\)
Tìm các giá trị nguyên của m để hàm số y= 1/3x³ - mx² + (2m+3)x +1 .đồng biến trên R
\(y'=\dfrac{1}{3}\cdot3x^2-m\cdot2x+2m+3=x^2-2m\cdot x+2m+3\)
Để hàm số đồng biến trên R thì y'>=0 với mọi x thuộc R
=>Δ=(-2m)^2-4(2m+3)<=0 và 1>0
=>4m^2-8m-12<=0
=>m^2-2m-3<=0
=>(m-3)(m+1)<=0
=>-1<=m<=3
mà m nguyên
nên \(m\in\left\{-1;0;1;2;3\right\}\)
Đúng 0
Bình luận (0)
Xét tính đơn điệu của hàm số: f(x) = x +\(\sqrt{x^2-4}\)
\(f\left(x\right)=x+\sqrt[]{x^2-4}\)
\(f\left(x\right)\) xác định khi và chỉ khi
\(x^2-4\ge0\Leftrightarrow x^2\ge4\Leftrightarrow x\le-2\cup x\ge2\)
Tập xác định : \(D=(-\infty;-2]\cup[2;+\infty)\)
\(f'\left(x\right)=1+\dfrac{x}{\sqrt[]{x^2-4}}\)
\(f'\left(x\right)=0\)
\(\Leftrightarrow1+\dfrac{x}{\sqrt[]{x^2-4}}=0\)
\(\Leftrightarrow\dfrac{\sqrt[]{x^2-4}+x}{\sqrt[]{x^2-4}}=0\)
\(\Leftrightarrow\sqrt[]{x^2-4}+x=0\left(x< -2;x>2\right)\)
Theo bất đẳng thức Bunhiacopxki:
\(\left(1.\sqrt[]{x^2-4}+1.x\right)^2\le2\left(2x^2+4\right)=4\left(x^2+2\right)\)
\(pt\Leftrightarrow4\left(x^2+2\right)=0\left(vô.lý\right)\)
\(\Rightarrow\) phương trình vô nghiệm
Đúng 1
Bình luận (0)
Tiếp tục bài giải, mình nhấn nút gửi
\(...\Rightarrow f'\left(x\right)>0,\forall x\in D\)
\(\Rightarrow f\left(x\right)\) luôn luôn tăng trên tập xác định D.
Đúng 1
Bình luận (0)
Xét tính đơn điệu của hàm số: f(x) = x + |3x2 + 9x -12|
Xét tính đơn điệu của hàm số:
a, f(x) = x + 2cosx trên (0;2π)
b, f(x) = |x2 - 3x + 2|
Xét tính đơn điệu của hàm số: f(x) = 2x - sin2x
\(f'\left(x\right)=2-2cos2x\)
\(f'\left(x\right)=0\Leftrightarrow x=0\)
Hàm số đồng biến trên khoảng \(\left(0;+\infty\right)\)
Hàm số nghịch biến trên khoảng \(\left(-\infty;0\right)\)
Đúng 1
Bình luận (0)
![]() BẠN NÀO CHO MIK BIẾT 1678327978+329783653348689:56432 =
BẠN NÀO CHO MIK BIẾT 1678327978+329783653348689:56432 =



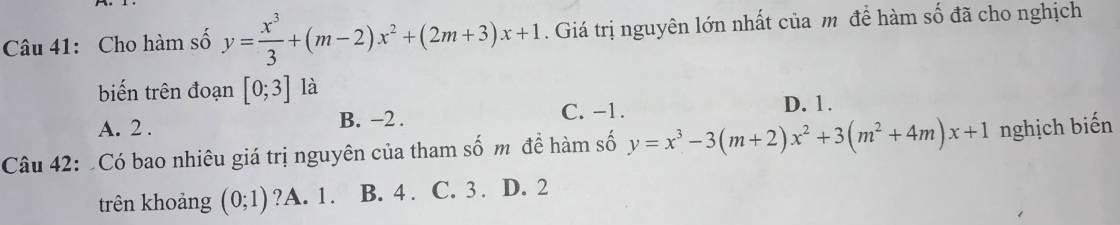

 chúc bạn học tốt
chúc bạn học tốt





