Em hãy lập kế hoạch cá nhân cho 1 tuần nghỉ TẾT
Cho 3 số a,b,c thỏa mãn:
a2 + b2 + c2 = a3 + b3 + c3 = 1
Tính S =a2 + b2017 + c2018 ☠ ☠ ☠
\(a^2+b^2+c^2=1\Rightarrow\left\{{}\begin{matrix}a^2\le1\\b^2\le1\\c^2\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\le1\\\left|b\right|\le1\\\left|c\right|\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^3\le a^2\\b^3\le b^2\\c^3\le c^2\end{matrix}\right.\)
\(\Rightarrow a^3+b^3+c^3\le a^2+b^2+c^2=1\)
Đẳng thức xảy ra khi và chỉ khi: \(\left(a;b;c\right)=\left(0;0;1\right)\) và các hoán vị
\(\Rightarrow S=0+0+1=1\)
Đúng 2
Bình luận (0)
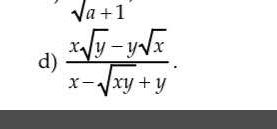rút gọn cái bài này giúp tớ
Cho hai tiếp tuyến AB, AC của đường tròn (O) (B, C là hai tiếp điểm). AO cắt BC tại H. Vẽ đường kính BD. Gọi M là trung điểm của AH. DN cắt (O) tại N. Chứng minh M, B, N thẳng hàng.(làm theo kiến thức lớp 9 ạ)
6. Cho hai tiếp tuyến AB, AC của đường tròn (O) (B, C là hai tiếp điểm). AO cắt BC tại H. Vẽ đường kính BD. Gọi M là trung điểm của AH. DN cắt (O) tại N. Chứng minh M, B, N thẳng hàng.(làm theo kiến thức lớp 9 ạ)
Cho (O,R) và (O',R') cắt nhau tại A,B ( O,O' khác phía với A,B). AO và AO' cắt (O) tại 2 điểm C,D và cắt (O') tại E,F. Chứng minh: ∠DBC = ∠EBF
Xét (O) có A,B,C,D cùng thuộc một đường tròn
nên ABCD là tứ giác nội tiếp
=>\(\widehat{DAC}=\widehat{DBC}\)
mà \(\widehat{DAC}=\widehat{EAF}\)(hai góc đối đỉnh)
nên \(\widehat{DBC}=\widehat{EAF}\)(1)
Xét (O') có A,E,F,B cùng thuộc (O')
nên AEFB là tứ giác nội tiếp
=>\(\widehat{EAF}=\widehat{EBF}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{DBC}=\widehat{EBF}\)
Đúng 1
Bình luận (0)
NH
13 tháng 1 lúc 21:50
Cho tam giác ABC nhọn, AB < AC. Vẽ AH vuông góc với BC (H thuộc BC). Trên tia AH lấy điểm K sao cho H là trung điểm của AK.
a) Chứng minh rằng ∆ACH=AKCH
(Làm giúp em phần c,d thôi ạ, em cảm ơn)
cho ba số thực dương x,y,z :(x-y).(y-z).(x-z)=9.Tính B=(x-y)^3+(y-z)^3+(x-z)^3
Sửa đề là z-x không phải x-z nhé!
Đặt: `a=x-y;b=y-z;c=z-x`
Ta có: `abc=9` và cần tính `B=a^3+b^3+c^3`
`B-3abc=a^3+b^3+c^3-3abc`
`=(a+b)^3-3ab(a+b)+c^3-3abc`
`=(a+b+c)[(a+b)^2-(a+b)c+c^2]-3ab(a+b+c)`
`=(a+b+c)(a^2+2ab+b^2-ab-ac+c^2-3ab)`
`=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)`
Mà: `a+b+c=x-y+y-z+z-x=0`
`=>B-3abc=0<=>B=3abc=3*9=27`
Đúng 1
Bình luận (0)
PL
13 tháng 1 lúc 21:06
Xem thêm câu trả lời
H24
13 tháng 1 lúc 21:00
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3 cm, cạnh bên SA vuông góc với mặt đáy, đường thẳng SD tạo với mặt đáy một góc 45 độ. Gọi M là trung điểm của cạnh CD. Khoảng cách từ điểm A đến mặt phẳng (SBM) bằng bao nhiêu cm?
H24
13 tháng 1 lúc 20:58
Tìm GTNN của hàm số \(y=x\sqrt{3}-cos2x\) trên đoạn \(\left[-\text{ }\dfrac{\text{π}}{4};0\right]\)