Cho tam giác nhọn AMN VẼ AH VUÔNG GÓC VỚI MN GỌI O LÀ MỘT ĐIỂM NẰM TRÊN ĐOẠN THẲNG AH BIẾT CHU VI TAM GIÁC AMN LÀ 38 VÀ MN = 8 TÌM GIÁ TRỊ LỚN NHẤT CỦA TỔNG OM + ON GIÚP VỚI PLS
Ôn tập Tam giác
Cho tam giác MNP cân tại P với góc P nhỏ hơn 90 độ và A là trung điểm của M N CÂU A CHỨNG MINH TAM GIÁC NAP BẰNG TAM GIÁC MAP VÀ PA VUÔNG GÓC VỚI MN câu b gọi B là trung điểm của PN và MB cắt PA Tại G . Tính AB và GB biết MP bằng 13 cm và MN = 10 cm câu c trên tia đối của tia BM LẤY ĐIỂM C SAO CHO BG = BC CHỨNG MINH CM LỚN HƠN CN GIÚP VỚI PLS
a: Xét ΔPAM và ΔPAN có
PA chung
AM=AN
PM=PN
Do đó: ΔPAM=ΔPAN
=>\(\widehat{PAM}=\widehat{PAN}\)
mà \(\widehat{PAM}+\widehat{PAN}=180^0\)
nên \(\widehat{PAM}=\widehat{PAN}=\dfrac{180^0}{2}=90^0\)
=>PA\(\perp\)MN
b: ta có: A là trung điểm của MN
=>\(MA=AN=\dfrac{MN}{2}=5\left(cm\right)\)
Xét ΔPAM vuông tại A có \(PA^2+AM^2=PM^2\)
=>\(PA^2=13^2-5^2=144=12^2\)
=>PA=12(cm)
Xét ΔNMP có
A,B lần lượt là trung điểm của NM,NP
=>AB là đường trung bình của ΔNMP
=>\(AB=\dfrac{MP}{2}=6,5\left(cm\right)\)
Đúng 2
Bình luận (1)
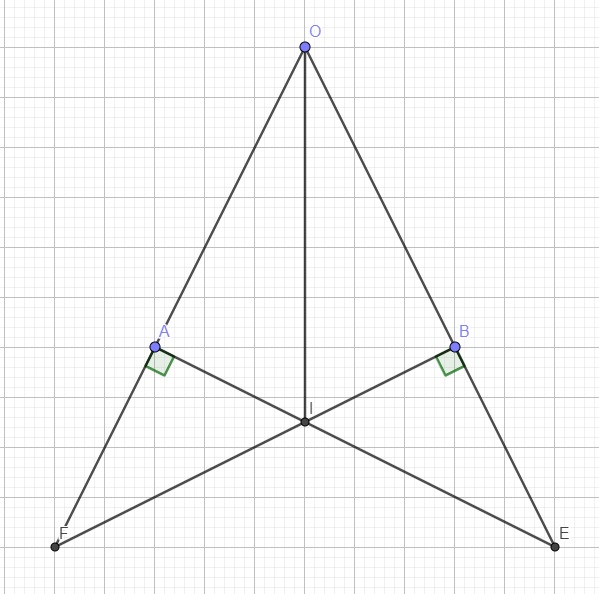
Cho góc nhọn xOy.Trên Ox,Oy lần lượt lấy 2 điểm A,B sao cho OA=OB.Từ A kẻ đường thẳng vuông góc với Ox cắt Oy tại E.Từ B kẻ đường thẳng vuông góc với Ox cắt Ox tại F.AE và BF cắt nhau tại I
Chứng minh:
a,AE=BF
b,tam giác AFI=tam giác BEI
c,OI là phân giác của AOB
Mong các bạn chữa bài này của mình nhé.
a.
Do \(BF\perp OE\left(gt\right)\Rightarrow\widehat{OBF}=90^0\)
Do \(AE\perp OF\Rightarrow\widehat{OAE}=90^0\)
Xét hai tam giác OAE và OBF có:
\(\left\{{}\begin{matrix}\widehat{O}-chung\\OA=OB\left(gt\right)\\\widehat{OAE}=\widehat{OBF}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta OAE=\Delta OBF\left(g.c.g\right)\)
\(\Rightarrow AE=BF\)
b.
Từ câu a, do \(\Delta OAE=\Delta OBF\Rightarrow OE=OF\)
\(\Rightarrow OB+BE=OA+AF\)
Mà \(OA=OB\Rightarrow BE=AF\)
Lại có \(\widehat{AIF}=\widehat{BIE}\) (hai góc đối đỉnh)
\(\Rightarrow90^0-\widehat{AFI}=90^0-\widehat{BEI}\) (các tam giác AFI và BEI vuông)
\(\Rightarrow\widehat{AFI}=\widehat{BEI}\)
Xét hai tam giác AFI và BEI có:
\(\left\{{}\begin{matrix}\widehat{AFI}=\widehat{BEI}\left(cmt\right)\\AF=BE\left(cmt\right)\\\widehat{IAF}=\widehat{IBE}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AFI=\Delta BEI\left(g.c.g\right)\)
c.
Từ câu b, do \(\Delta AFI=\Delta BEI\Rightarrow AI=BI\)
Xét hai tam giác OAI và OBI có:
\(\left\{{}\begin{matrix}OA=OB\left(gt\right)\\OI-chung\\AI=BI\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta OAI=\Delta OBI\left(c.c.c\right)\)
\(\Rightarrow\widehat{AOI}=\widehat{BOI}\)
\(\Rightarrow OI\) là phân giác góc \(\widehat{AOB}\)
Đúng 1
Bình luận (0)
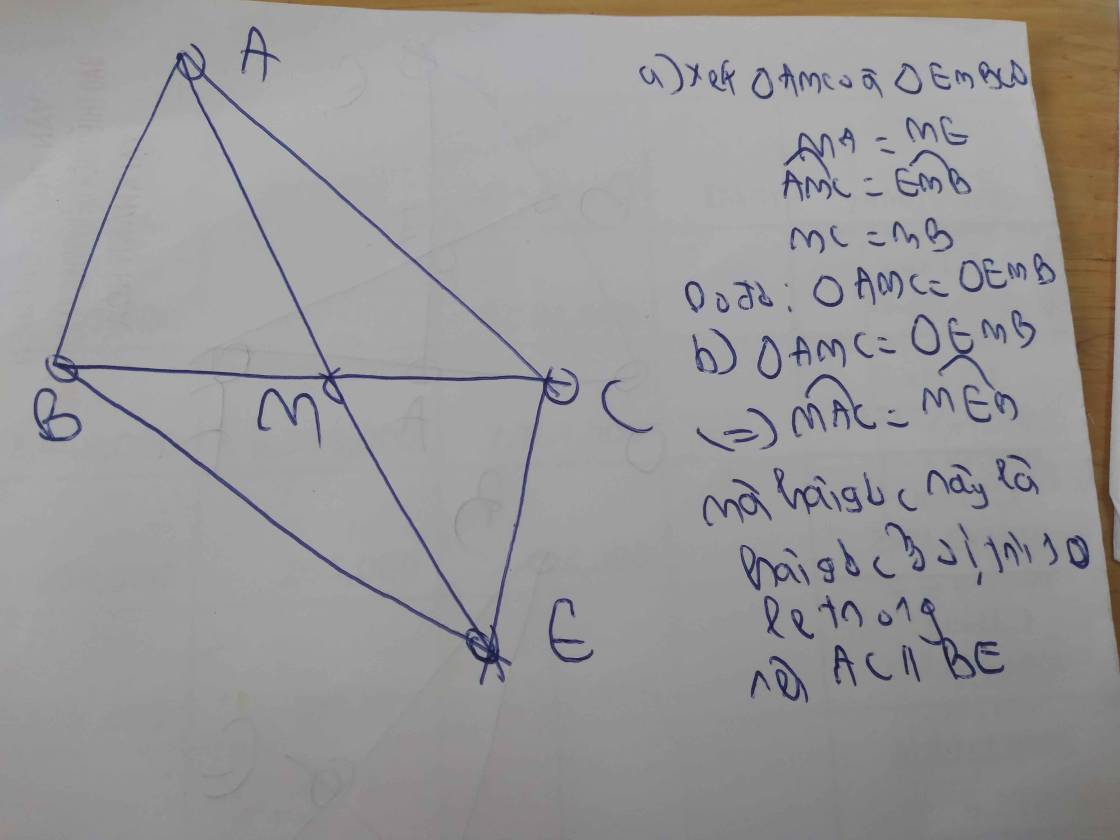
Cho tam giác ABC,M là trung điểm của BC.Trên tia AM lấy điểm E sao cho AM=ME
a)Chứng minh tam giác AMC=tam giác EMB
b)Chứng minh AC song song với BE
(Trả lời và vẽ hình giúp mik với ạ ! Mình xin chân thành cảm ơn)
Cho tam giác ABC có góc ABC =35°; góc ACB =65° a, Tính số đo góc BAC b, Tìm cạnh lớn nhất và bé nhất của tam giác ABC c, Vẽ AI vuông góc với BC ( I thuộc cạnh BC ). Trên đoạn AI lấy điểm D, trên đoạn IB lấy điểm E. Chứng minh DE < AB
a: Xét ΔABC có
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{BAC}+35^0+65^0=180^0\)
=>\(\widehat{BAC}=80^0\)
b: Xét ΔABC có \(\widehat{BAC}>\widehat{ACB}>\widehat{ABC}\)
mà BC,AB,AC lần lượt là cạnh đối diện của các góc BAC;ACB;ABC
nên BC>AB>AC
=>Cạnh lớn nhất là BC, cạnh nhỏ nhất là AC
c: Xét ΔIDE có \(\widehat{ADE}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADE}=\widehat{DIE}+\widehat{DEI}=90^0+\widehat{DEI}>90^0\)
Xét ΔADE có \(\widehat{ADE}>90^0\)
nên AE là cạnh lớn nhất
=>AE>DE
Xét ΔAIE có \(\widehat{AEB}\) là góc ngoài tại đỉnh E
nên \(\widehat{AEB}=\widehat{EIA}+\widehat{EAI}=90^0+\widehat{EAI}>90^0\)
Xét ΔAEB có \(\widehat{AEB}>90^0\)
nên AB là cạnh lớn nhất trong ΔAEB
=>AB>AE
mà AE>DE
nên DE<AB
Đúng 0
Bình luận (0)
a: Xét ΔMNP và ΔPQM có
MN=PQ
NP=QM
MP chung
Do đó: ΔMNP=ΔPQM
b: ΔMNP=ΔPQM
=>\(\widehat{NMP}=\widehat{QPM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên MN//QP
Ta có: ΔMNP=ΔPQM
=>\(\widehat{MPN}=\widehat{PMQ}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NP//MQ
Đúng 3
Bình luận (0)
a) Xét ΔDAB và ΔBDC có:
\(AB=CD\)
\(BD\) chung
\(\widehat{ABD}=\widehat{BDC}\) (cặp góc so le trong vì AB//CD)
\(\Rightarrow\text{Δ}ABD=\text{Δ}CDB\left(c.g.c\right)\)
b) Xét ΔDAC và ΔBCA có:
\(\widehat{DCA}=\widehat{BAC}\) (cặp góc so le trong vì AB//CD)
\(AC\) chung
\(AB=CD\)
\(\Rightarrow\text{Δ}DAC=\text{Δ}BCA\left(c.g.c\right)\)
Đúng 2
Bình luận (0)
Ta có:
3,8m+3,3m=7,1m > 3,4m
3,3m+3,4m=6,7m > 3,8m
3,4m+3,8m=7,2m > 3,3m
Vậy theo bất đẳng thức tam giác thì bộ ba độ dài đoạn thẳng trên là cạnh của tam giác.
Đúng 1
Bình luận (0)
Ta có:
3,3 + 3,4 = 6,7 > 3,8
Vậy bộ ba độ dài đoạn thẳng 3,8 m; 3,3 m; 3,4 m có thể là ba cạnh của tam giác
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM CN.a) chứng minh tam giác AMN cân.b) kẻ BE vuông góc AM, CF vuông góc AN. chứng minh tam giác BME tam gác CNF. c) EB và FC kéo dài cắt nhau tại O . chứng minh AO là tia phân giác của góc MAN.
Đọc tiếp
Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.
a) chứng minh tam giác AMN cân.b) kẻ BE vuông góc AM, CF vuông góc AN. chứng minh tam giác BME = tam gác CNF. c) EB và FC kéo dài cắt nhau tại O . chứng minh AO là tia phân giác của góc MAN.a: Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
b: Xét ΔEMB vuông tại E và ΔFNC vuông tại F có
BM=CN
\(\widehat{EMB}=\widehat{FNC}\)(ΔAMN cân tại A)
Do đó: ΔEMB=ΔFNC
c: Ta có: \(\widehat{EBM}=\widehat{OBC}\)(hai góc đối đỉnh)
\(\widehat{FCN}=\widehat{OCB}\)(hai góc đối đỉnh)
mà \(\widehat{EBM}=\widehat{FCN}\)(ΔEBM=ΔFCN)
nên \(\widehat{OBC}=\widehat{OCB}\)
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC
=>AO\(\perp\)MN
Ta có: ΔAMN cân tại A
mà AO là đường cao
nên AO là phân giác của góc MAN
Đúng 2
Bình luận (0)
Bài 4: Cho ABC nhọn, trên nửa mp bờ AB không chứa C, dựng đoạn thẳng AD vuông góc với AB và AD AB, trên nửa mp bờ AC không chứa B, dừng AE vuông góc AC và AEAC, vẽ AH vuông góc với BC, đường thẳng HA cắt DE ở K, CMR: K là trung điểm của DE
Đọc tiếp
Bài 4: Cho ![]() ABC nhọn, trên nửa mp bờ AB không chứa C, dựng đoạn thẳng AD vuông góc với AB và AD= AB, trên nửa mp bờ AC không chứa B, dừng AE vuông góc AC và AE=AC, vẽ AH vuông góc với BC, đường thẳng HA cắt DE ở K, CMR: K là trung điểm của DE
ABC nhọn, trên nửa mp bờ AB không chứa C, dựng đoạn thẳng AD vuông góc với AB và AD= AB, trên nửa mp bờ AC không chứa B, dừng AE vuông góc AC và AE=AC, vẽ AH vuông góc với BC, đường thẳng HA cắt DE ở K, CMR: K là trung điểm của DE