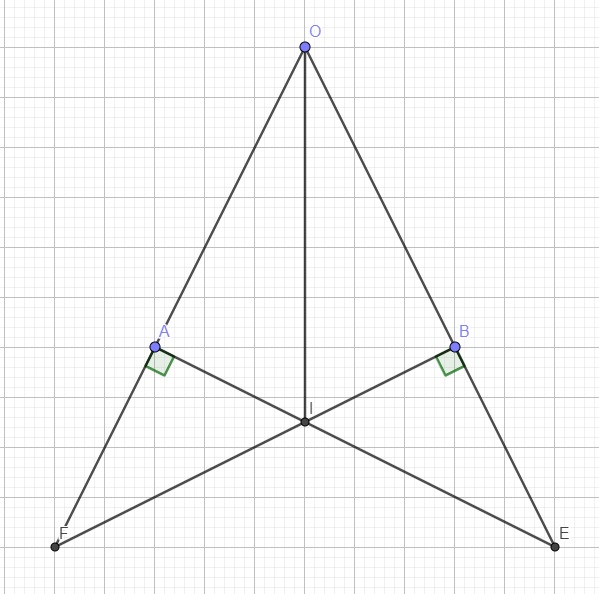
a.
Do \(BF\perp OE\left(gt\right)\Rightarrow\widehat{OBF}=90^0\)
Do \(AE\perp OF\Rightarrow\widehat{OAE}=90^0\)
Xét hai tam giác OAE và OBF có:
\(\left\{{}\begin{matrix}\widehat{O}-chung\\OA=OB\left(gt\right)\\\widehat{OAE}=\widehat{OBF}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta OAE=\Delta OBF\left(g.c.g\right)\)
\(\Rightarrow AE=BF\)
b.
Từ câu a, do \(\Delta OAE=\Delta OBF\Rightarrow OE=OF\)
\(\Rightarrow OB+BE=OA+AF\)
Mà \(OA=OB\Rightarrow BE=AF\)
Lại có \(\widehat{AIF}=\widehat{BIE}\) (hai góc đối đỉnh)
\(\Rightarrow90^0-\widehat{AFI}=90^0-\widehat{BEI}\) (các tam giác AFI và BEI vuông)
\(\Rightarrow\widehat{AFI}=\widehat{BEI}\)
Xét hai tam giác AFI và BEI có:
\(\left\{{}\begin{matrix}\widehat{AFI}=\widehat{BEI}\left(cmt\right)\\AF=BE\left(cmt\right)\\\widehat{IAF}=\widehat{IBE}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AFI=\Delta BEI\left(g.c.g\right)\)
c.
Từ câu b, do \(\Delta AFI=\Delta BEI\Rightarrow AI=BI\)
Xét hai tam giác OAI và OBI có:
\(\left\{{}\begin{matrix}OA=OB\left(gt\right)\\OI-chung\\AI=BI\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta OAI=\Delta OBI\left(c.c.c\right)\)
\(\Rightarrow\widehat{AOI}=\widehat{BOI}\)
\(\Rightarrow OI\) là phân giác góc \(\widehat{AOB}\)