Ôn tập Tam giác

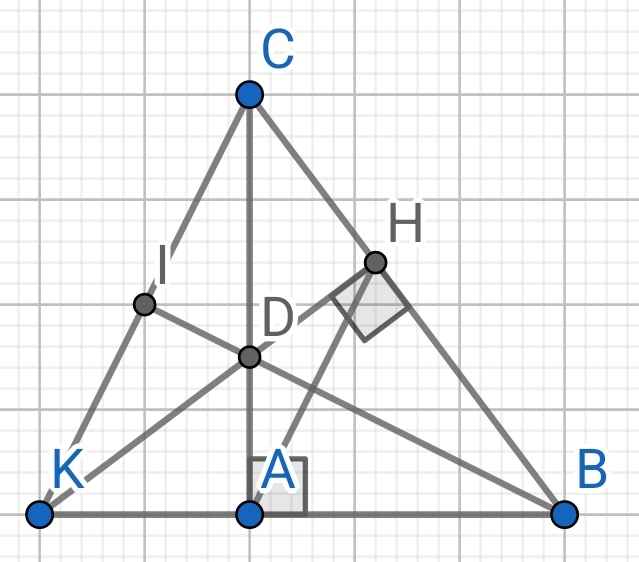
Do BD là tia phân giác của ∠ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠HBD

Xét hai tam giác vuông: ∆ABD và ∆HBD có:

BD là cạnh chung

∠ABD = ∠HBD (cmt)

⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)

⇒ AD = DH (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆ADK và ∆HDC có:

AD = DH (cmt)

∠ADK = ∠HDC (đối đỉnh)

⇒ ∆ADK = ∆HDC (cạnh góc vuông - góc nhọn kề)

⇒ AK = HC (hai cạnh tương ứng)

Do ∆ABD = ∆HBD (cmt)

⇒ AB = HB (hai cạnh tương ứng)

Mà AK = HC (cmt)

⇒ AB + AK = HB + HC

⇒ BK = BC

Do I là trung điểm của KC (gt)

⇒ IK = IC

Xét ∆BCI và ∆BKI có:

BC = BK (cmt)

IC = IK (cmt)

BI là cạnh chung

⇒ ∆BCI = ∆BKI (c-c-c)

⇒ ∠IBC = ∠IKC (hai góc tương ứng)

⇒ BI là tia phân giác của ∠KBC

⇒ BI là tia phân giác của ∠ABC

Mà BD là tia phân giác của ∠ABC (gt)

⇒ B, D, I thẳng hàng

Sửa đề:cho tam giác abc vuông tại a dường phân giác bd  ( d thuộc ac ) từ d kẻ dh vuông góc với bc gọi k là giao điểm của đường thẳng ab và hd,i là trung điểm của kc . chứng minh 3 điểm b,d,i thẳng hàng

                                                                                            Giải

Xét △BAD và △BHD có:BD chung

                                       DAB^=DHB^=90°

                                       ABD^=HBD^

⇒△BAD = △BHD

⇒BA=BH

Xét △BAC và △BHK có: BA=BH

                                        BHK^=BAC^=90°

                                        B^ chung

⇒△BAC = △BHK

⇒BK=BC

Xét △BIC và △BIK có: IK=IC

                                    BK=BC

                                     BI chung

⇒△BIC = △BIK

⇒BIK^=BIC^

mà 2 góc này là 2 góc kề bù

⇒BIK^=BIC^=90°

⇒BI⊥KC (1)

△BKC có:KH⊥BC

                CA⊥BK

               KH cắt CA tại D

⇒D là trực tâm △BKC

Vì D là trực tâm △BKC nên đường cao thứ 3 đi qua D

mà đường cao thứ 3 của △BKC là BI(Do BI⊥KC)

⇒B,D,I thẳng hàng

Sửa đề:Cho tam giác abc vuông tại a dường phân giác bc  ( d thuộc ac ) từ d  góc với bc kẻ dh vuông. gọi k là giao điểm của đường thẳng ab và dh. i là trung điểm của kc và dh . chứng minh 3 điểm b,d,i thẳng hàng

                                                        Giải

△BKC có:KH⊥BC

                CA⊥BK

                KH cắt CA tại D

⇒D là trực tâm của △BKC

⇒BD⊥KC (1)

Xét △ vuông ABD và △ vuông AHD có:AD chung

                                                               ABD^=HAD^(BD là p/g BAC^)

⇒△ vuông ABD = △ vuông AHD

⇒BA=BH

Xét △ vuông BKH và △ vuông BAC có:B^chung

                                                               BA=BH

⇒△ vuông BKH = △ vuông BAC

⇒BK=BC

⇒△BKC cân tại B

Vì BI là trung tuyến của △ cân BKC ⇒BI⊥KC(2)

Từ (1) và (2)⇒B,D,I  thẳng hàng

đề sai r bn ạ 

Ta có tam giác OMN cân tại O do OM = ON 

Lại có NF là đường cao; ME là đường cao 

mà NF giao ME tại G 

=> G là trực tâm 

Xét tam giác OMN có OG là đường cao 

=> OG đồng thời là đường pg => ^MOG = 1/2^xOy = 36⁰

a: Ta có: ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-\widehat{BAC}}{2}=65^0\)

Xét ΔABC có \(\widehat{ACB}>\widehat{BAC}\)

mà AB,BC lần lượt là cạnh đối diện của các góc ACB,BAC

nên AB>BC

b: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

c: ta có: ΔABM=ΔACM

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AM\(\perp\)BC
 

Em ghi thiếu đề rồi, đề phải có thêm 1 dữ kiện về độ dài cạnh AC hoặc góc B, góc C

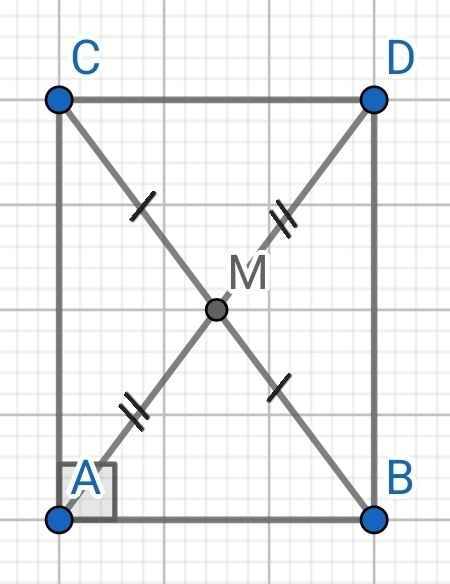
a) Do M là trung điểm của BC (gt)

⇒ MB = MC

Xét ∆AMB và ∆DMC có:

AM = DM (gt)

∠AMB = ∠DMC (đối đỉnh)

MB = MC (cmt)

⇒ ∆AMB = ∆DMC (c-g-c)

⇒ ∠MAB = ∠MDC (hai góc tương ứng)

Lại có:

∠MAC + ∠MAB = 90⁰ (∆ABC vuông tại A)

⇒ ∠MAC + ∠MDC = 90⁰

⇒ ∠DAC + ∠ADC = 90⁰

∆CDA có:

∠DAC + ∠CDA + ∠ACD = 180⁰ (tổng ba góc trong ∆ACD)

⇒ ∠ACD = 180⁰ - (∠DAC + ∠CDA)

= 180⁰ - 90⁰

= 90⁰

⇒ ∆ACD vuông tại C

Do ∆AMB = ∆DMC (cmt)

⇒ AB = CD (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆ABC và ∆CDA có:

AC là cạnh chung

AB = CD (cmt)

⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)

b) Do ∆ABC = ∆CDA (cmt)

⇒ BC = AD (hai cạnh tương ứng)

Do AM = DM (gt)

⇒ AM = DM = ½AD

Mà AD = BC (cmt)

⇒ AM = ½BC

a: Xét tứ giác ABDC có 

M là trung điểm của AD

M là trung điểm của BC

DO đó: ABDC là hình bình hành

Suy ra: AB=DC; AC=BD

Xét ΔABC và ΔCDA có 

AB=CD

BC=DA

AC chung

Do đó: ΔABC=ΔCDA

b: Ta có: ΔABC vuông tại A

mà AM là đường trung tuyến

nên AM=1/2BC

E nằm trên đường trung trực của MN

=>EM=EN

=>ΔEMN cân tại E

=>\(\widehat{EMN}=\widehat{ENM}\)

F nằm trên đường trung trực của MP

=>FM=FP

=>ΔFMP cân tại F

=>\(\widehat{FMP}=\widehat{FPM}\)

Ta có: \(\widehat{EMN}+\widehat{FMP}=\widehat{N}+\widehat{P}\)

\(=180^0-\widehat{NMP}=40^0\)

Ta có: \(\widehat{EMN}+\widehat{FMP}+\widehat{EMF}=\widehat{NMP}\)

=>\(\widehat{EMF}+40^0=140^0\)

=>\(\widehat{EMF}=100^0\)