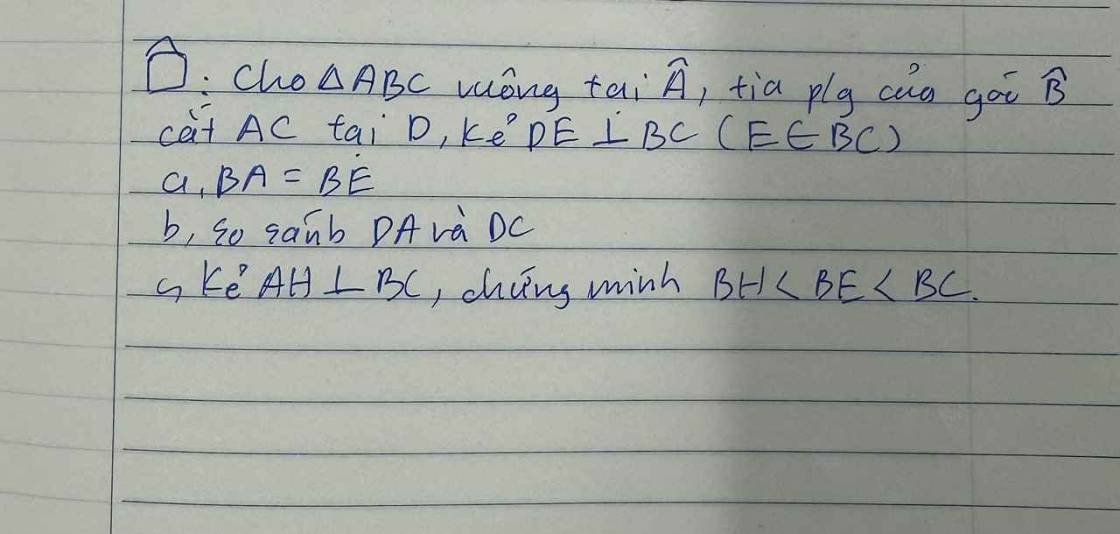
Ôn tập Tam giác

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

=>BA=BE

b: ta có: ΔBAD=ΔBED

=>DA=DE
mà DE<DC

nên DA<DC
c: Ta có: ΔBAH vuông tại H

=>BH<BA

mà BA=BE

nên BH<BE(1)

Ta có: ΔBAC vuông tại A

=>BA<BC

mà BE=BA

nên BE<BC(2)

từ (1) và (2) suy ra BH<BE<BC

Sửa đề: Lấy E thuộc BC sao cho BE=BA

a: Chứng minh ΔBAD=ΔBED

Xét ΔBAD và ΔBED có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED

b: ta có: ΔBAD=ΔBED

=>\(\widehat{BAD}=\widehat{BED}\)

mà \(\widehat{BAD}=90^0\)

nên \(\widehat{BED}=90^0\)

=>DE\(\perp\)BC

=>ΔDEC vuông tại E

c: Sửa đề: Tia BA cắt ED tại F

Ta có: ΔBAD=ΔBED

=>DA=DE

Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó: ΔDAF=ΔDEC

=>AF=EC

d.

Theo chứng minh câu c ta có tam giác NPO cân tại N

Mà I là trung điểm OP \(\Rightarrow NI\) là đường trung tuyến

Trong tam giác NPO cân tại N, NI là trung tuyến nên nó đồng thời là phân giác góc \(\widehat{ONP}\)

Hay NI là phân giác trong góc \(\widehat{MNP}\)

Lại có ND cũng là phân giác trong góc \(\widehat{MNP}\) (giả thiết)

\(\Rightarrow\) Đường thẳng NI trùng đường thẳng ND

Hay 3 điểm N, D, I thẳng hàng

a: Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

b: Xét ΔBFC có

BH là đường cao
BH là đường phân giác

Do đó: ΔBFC cân tại B

c: Ta có: ΔBFC cân tại B

=>BF=BC

Xét ΔBDF và ΔBAC có

BD=BA

\(\widehat{DBF}\) chung

BF=BC

Do đó: ΔBDF=ΔBAC

=>\(\widehat{BDF}=\widehat{BAC}=90^0\)

Ta có: ΔBAE=ΔBDE

=>\(\widehat{BAE}=\widehat{BDE}\)

mà \(\widehat{BAE}=90^0\)

nên \(\widehat{BDE}=90^0\)

mà \(\widehat{BDF}=90^0\)

và DE,DF có điểm chung là D

nên D,E,F thẳng hàng

Đề thiếu yêu cầu. Bạn xem lại

Câu 1: 

a. Xét tam giác $ABM$ và $DCM$ có:

$BM=CM$ (do $M$ là trung điểm $AB$)

$AM=MD$ (gt)

$\widehat{AMB}=\widehat{DMC}$ (đối đỉnh)

$\Rightarrow \triangle ABM=\triangle DCM$ (c.g.c)

b.

Từ tam giác bằng nhau phần a suy ra $\widehat{ABM}=\widehat{DCM}$

Mà 2 góc này ở vị trí so le trong nên $AB\parallel CD$

c. 

Xét tam giác $ABM$ và $ACM$ có:

$AB=AC$

$BM=CM$

$AM$ chung

$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)

$\Rightarrow \widehat{AMB}=\widehat{AMC}$ 

Mà 2 góc này kề bù nên $\widehat{AMB}=\widehat{AMC}=90^0$

$\Rightarrow AM\perp BC$ hay $AM\perp BC$

Mà $M$ là trung điểm của $BC$ nên $AM$ là trung trực của $BC$

Hình vẽ:

Câu 2 bạn xem lại đề nhé.

Sửa đề: cắt MN tại K

a: Xét ΔAHM và ΔAHN có

AH chung

\(\widehat{HAM}=\widehat{HAN}\)

AM=AN

Do đó: ΔAHM=ΔAHN

b: Ta có: ΔAHM=ΔAHN

=>HM=HN

Ta có: ΔAMN cân tại A

mà AK là đường phân giác

nên K là trung điểm của MN

=>KM=KN

Xét ΔHKM và ΔHKN có

HK chung

KM=KN

HM=HN

Do đó: ΔHKM=ΔHKN

a: Xét ΔBAE và ΔBFE có

BA=BF

\(\widehat{ABE}=\widehat{FBE}\)

BE chung

Do đó: ΔBAE=ΔBFE

b: Ta có: ΔBAE=ΔBFE

=>\(\widehat{BAE}=\widehat{BFE}\)

mà \(\widehat{BAE}=90^0\)

nên \(\widehat{BFE}=90^0\)

=>EF\(\perp\)BC

c: Xét ΔAEM và ΔFEC có

EA=EF

\(\widehat{AEM}=\widehat{FEC}\)

EM=EC

Do đó: ΔAEM=ΔFEC

=>\(\widehat{EAM}=\widehat{EFC}\)

mà \(\widehat{EFC}=90^0\)

nên \(\widehat{EAM}=90^0\)

Ta có: \(\widehat{BAM}=\widehat{BAE}+\widehat{MAE}\)

\(=90^0+90^0=180^0\)

=>B,A,M thẳng hàng

a: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

b: Ta có: ΔABM=ΔACM

=>\(\widehat{BAM}=\widehat{CAM}\)

=>\(\widehat{DAM}=\widehat{EAM}\)

Xét ΔDAM và ΔEAM có

DA=EA

\(\widehat{DAM}=\widehat{EAM}\)

AM chung

Do đó: ΔDAM=ΔEAM

=>MD=ME

c: Xét ΔNKD và ΔNMB có

NK=NM

\(\widehat{KND}=\widehat{MNB}\)(hai góc đối đỉnh)

ND=NB

Do đó: ΔNKD=ΔNMB

=>\(\widehat{NKD}=\widehat{NMB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên KD//BM

mà M\(\in\)BC

nên KD//BC

Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)

nên DE//BC

Ta có: KD//BC

DE//BC

KD,DE có điểm chung là D

Do đó: K,D,E thẳng hàng

a: Xét ΔMAD và ΔMCB có

MA=MC

\(\widehat{AMD}=\widehat{CMB}\)(hai góc đối đỉnh)

MD=MB

Do đó: ΔMAD=ΔMCB

=>AD=BC

b: Xét ΔMAB và ΔMCD có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

MB=MD

Do đó: ΔMAB=ΔMCD

=>\(\widehat{MAB}=\widehat{MCD}=90^0\)

=>CD\(\perp\)CA

c: Xét tứ giác ABNC có

AB//NC

AC//BN

Do đó: ABNC là hình bình hành

=>AB=CN

Xét ΔABM vuông tại A và ΔCNM vuông tại C có

AB=CN

AM=CM

Do đó: ΔABM=ΔCNM