cho tam giác abc, đường cao ah. gọi I là trung điiểm ac. lấy d là điểm sao cho I là trung điểm của HD. C/m tứ giác ahcd là hcn
Bài 9: Hình chữ nhật
Xét tứ giác AHCN, có:
IH = ID (gt)
IA = IC (gt)
=> tứ giác AHCN là hình bình hành
lại có \(\widehat{AHC}=90^0\)
=> hình bình hành AHCN là hình chữ nhật
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Lấy điểm M thuộc đoạn thẳng OC. Gọi E, F lần lượt là hình chiếu của điểm M trên đường thẳng AB, AD. Chứng minh:
a) Tứ giác AEMF là hình chữ nhật.
b) BD // EF.
+ vẽ hình nhé
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{EAF}=90^0\)
=>AEMF là hình chữ nhật
b:
Ta có: MF\(\perp\)AD
DC\(\perp\)AD
Do đó: MF//DC
Ta có: AEMF là hình chữ nhật
=>\(\widehat{AEF}=\widehat{AMF}\)
mà \(\widehat{AMF}=\widehat{ACD}\)(hai góc đồng vị, MF//CD)
nên \(\widehat{AEF}=\widehat{ACD}\)
Ta có: ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>O là trung điểm chung của AC và BD và AC=BD
=>OA=OB=OC=OD
Xét ΔACD vuông tại D và ΔCAB vuông tại B có
CA chung
AD=CB
Do đó: ΔACD=ΔCAB
=>\(\widehat{ACD}=\widehat{CAB}\)
mà \(\widehat{CAB}=\widehat{OAB}=\widehat{OBA}\)(ΔOAB cân tại O)
nên \(\widehat{ACD}=\widehat{ABD}\)
=>\(\widehat{AEF}=\widehat{ABD}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên EF//BD
Đúng 1
Bình luận (0)
Cho tam giác vuông ABC (A = 90°). Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng với M qua AB và AC. Gọi I, K lần lượt là giao điểm của MẸ với AB và MF với AC. Chứng minh:
a) MIAK là hình chữ nhật.
b) A là trung điểm của EF.
a: M đối xứng E qua AB
=>AB là đường trung trực của ME
=>AB\(\perp\)ME tại I và I là trung điểm của ME
Ta có: M đối xứng F qua AC
=>AC là đường trung trực của MF
=>AC\(\perp\)MF tại K và K là trung điểm của MF
Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
=>AIMK là hình chữ nhật
b: Ta có: AKMI là hình chữ nhật
=>AK//MI và AK=MI; KM//AI và KM=AI
Ta có: MI//AK
I\(\in\)ME
Do đó: IE//AK
Ta có: AK=IM
IM=IE
Do đó: AK=IE
Ta có: AI=MK
MK=KF
Do đó: AI=KF
Ta có: AI//MK
K\(\in\)MF
Do đó: AI//KF
Xét tứ giác AKIE có
AK//IE
AK=IE
Do đó: AKIE là hình bình hành
=>KI//AE và KI=AE
Xét tứ giác AIKF có
AI//KF
AI=KF
Do đó: AIKF là hình bình hành
=>KI//AF và KI=AF
Ta có: KI//AF
KI//AE
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
Ta có: KI=AE
KI=AF
Do đó: AE=AF
mà E,A,F thẳng hàng
nên A là trung điểm của EF
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A(AB<AC) .Gọi M là trung điểm BC.Kẻ MQ vuông góc AB,MK vuông góc AC
Xem chi tiết
a) Chứng minh tứ giác QMKA là hình chữ nhật
b) Gọi E là điểm đối xứng của M qua K.Chứng minh tứ giác AMCE là hình thoi
Cứu em bài này
a: Xét tứ giác AQMK có
\(\widehat{AQM}=\widehat{AKM}=\widehat{KAQ}=90^0\)
=>AQMK là hình chữ nhật
b: Xét ΔABC có
M là trung điểm của BC
MK//AB
Do đó: K là trung điểm của AC
Xét tứ giác AMCE có
K là trung điểm chung của AC và ME
=>AMCE là hình bình hành
Hình bình hành AMCE có AC\(\perp\)ME
nên AMCE là hình thoi
Đúng 0
Bình luận (0)
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, D là điểm đối xứng với H qua I. a. Tứ giác AHCE là hình gì? Vì sao? b. Tính độ dài HI nếu AH=6cm và AD = 8cm
a: Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
b: Ta có: AHCD là hình chữ nhật
=>\(AC^2=AD^2+AH^2\)
=>\(AC^2=6^2+8^2=100\)
=>\(AC=\sqrt{100}=10\left(cm\right)\)
Ta có: ΔAHC vuông tại H
mà HI là đường trung tuyến
nên \(HI=\dfrac{AC}{2}=5\left(cm\right)\)
Đúng 2
Bình luận (0)
cho ∆ABC ⊥ tại A. Gọi M là trung điểm BC
a) Với AB = 6cm; AC = 8cm tính BC, AM.
b) Gọi E đối xứng với A qua M. Chứng minh ABEC là hình chữ nhật.
c) Gọi H là hình chiếu của A lên BC. Kẻ HI ⊥ với AB tại I, K là hình chiếu của H lên AC. Gọi O là giao điểm AH và Ik, N là hình chiếu của H lên An. Chứng minh AH = IK, NO = ½IK
d) góc INK = ?
a) Với ∆ABC ⊥ tại A và M là trung điểm BC, ta có:
- Theo định lý Pythagoras, ta có: AB^2 + AC^2 = BC^2
- Thay giá trị vào, ta có: 6^2 + 8^2 = BC^2
- Tính toán, ta có: 36 + 64 = BC^2
- Tổng cộng, BC^2 = 100
- Vì BC là độ dài, nên BC = √100 = 10cm
- Vì M là trung điểm BC, nên AM = MC = 10/2 = 5cm
b) Để chứng minh ABEC là hình chữ nhật, ta cần chứng minh AB // EC và AB = EC.
- Vì M là trung điểm BC, nên AM = MC.
- Vì ∆ABC ⊥ tại A, nên góc BAC = 90 độ.
- Vì M là trung điểm BC, nên BM = MC.
- Vì BM = MC và góc BAC = 90 độ, nên ∆BAM ≅ ∆CAM theo góc-góc-góc.
- Từ đó, ta có AB = AC và góc BAM = góc CAM.
- Vì AB = AC và góc BAM = góc CAM, nên ∆ABM ≅ ∆ACM theo cạnh-góc-cạnh.
- Từ đó, ta có góc AMB = góc AMC và BM = MC.
- Vì góc AMB = góc AMC và BM = MC, nên ∆BME ≅ ∆CME theo góc-góc-góc.
- Từ đó, ta có góc BME = góc CME và BM = MC.
- Vì góc BME = góc CME và BM = MC, nên BM // EC.
- Vì BM // EC và AB = AC, nên AB // EC và AB = EC.
- Từ đó, ta có ABEC là hình chữ nhật.
c) Để chứng minh AH = IK và NO = 1/2 IK, ta cần chứng minh ∆AHN ≅ ∆IKO.
- Vì AH ⊥ BC và IK ⊥ AB, nên góc HAN = góc KIO = 90 độ.
- Vì AH ⊥ BC và HN ⊥ AN, nên góc HAN = góc HNA.
- Vì IK ⊥ AB và KO ⊥ AO, nên góc KIO = góc KOI.
- Vì góc HAN = góc HNA và góc KIO = góc KOI, nên ∆AHN ≅ ∆IKO theo góc-góc-góc.
- Từ đó, ta có AH = IK và NO = 1/2 IK.
d) Vì ∆AHN ≅ ∆IKO, nên góc INK = góc HNO.
- Vì NO = 1/2 IK, nên góc HNO = góc INK.
- Từ đó, ta có góc INK = góc HNO.
Đúng 1
Bình luận (3)
a: AI là phân giác của góc BAD
=>\(\widehat{BAI}=\widehat{DAI}\)
mà \(\widehat{BAI}=\widehat{AID}\)(hai góc so le trong, AB//DI)
nên \(\widehat{DAI}=\widehat{DIA}\)
=>DA=DI
AI là phân giác của góc BAD
=>\(\widehat{BAI}=\widehat{DAI}=\dfrac{1}{2}\cdot\widehat{BAD}=60^0\)
Xét ΔDAI có DA=DI và \(\widehat{DAI}=60^0\)
nên ΔDAI đều
=>AI=ID
mà \(ID=\dfrac{DC}{2}\)
nên \(AI=\dfrac{DC}{2}\)
Xét ΔADC có
AI là đường trung tuyến
\(AI=\dfrac{DC}{2}\)
Do đó: ΔADC vuông tại A
=>AD\(\perp\)AC
b: ABCD là hình bình hành
=>\(\widehat{D}+\widehat{BAD}=180^0\)
=>\(\widehat{D}+120^0=180^0\)
=>\(\widehat{D}=60^0\)
ABCD là hình bình hành
=>\(\widehat{B}=\widehat{D}=60^0\)
mà \(\widehat{IAB}=60^0\)
nên \(\widehat{IAB}=\widehat{CBA}\)
Xét tứ giác ABCI có AB//CI
nên ABCI là hình thang
Hình thang ABCI có \(\widehat{IAB}=\widehat{ABC}\)
nên ABCI là hình thang cân
c: Xét ΔADC vuông tại A có \(cosDAC=\dfrac{AD}{DC}\)
=>\(\dfrac{AD}{DC}=cos60=\dfrac{1}{2}\)
=>\(AD=\dfrac{1}{2}DC=DI=IC\)
AD=IC
AD=BC
Do đó: CI=CB
=>ΔCBI cân tại C
=>\(\widehat{CBI}=\widehat{CIB}\)
mà \(\widehat{CIB}=\widehat{ABI}\)(hai góc so le trong, AB//CI)
nên \(\widehat{ABI}=\widehat{CBI}\)
=>BI là phân giác của góc ABC
Đúng 1
Bình luận (0)
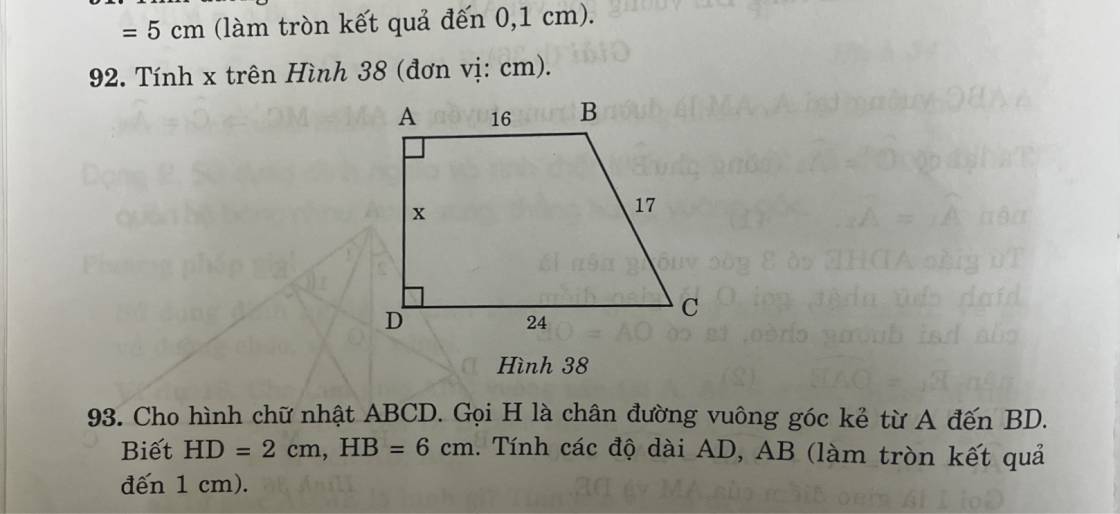
92:
Kẻ BH\(\perp\)DC tại H
Xét tứ giác ABHD có
\(\widehat{BHD}=\widehat{BAD}=\widehat{ADH}=90^0\)
=>ABHD là hình chữ nhật
=>AB=HD=16cm
HD+HC=CD
=>HC+16=24
=>HC=8cm
ΔBHC vuông tại H
=>\(BH^2+HC^2=BC^2\)
=>\(BH^2+8^2=17^2\)
=>\(BH^2+64=289\)
=>\(BH^2=225\)
=>BH=15(cm)
ABHD là hình chữ nhật
=>AD=BH=15(cm)
=>x=15(cm)
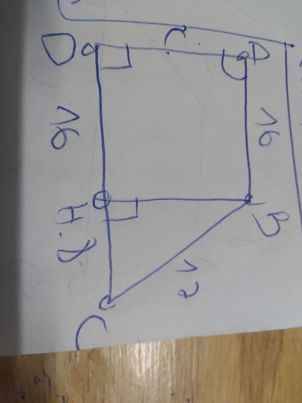
93:
BD=BH+DH
=6+2
=8(cm)
Xét ΔABD vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BD\\AD^2=DH\cdot DB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB^2=6\cdot8=48\\AD^2=2\cdot8=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=4\sqrt{3}\left(cm\right)\\AD=4\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho tam giác abc gọi m là điểm bất kì trên cạnh bc. kẻ mh vuông ab mk vuông ac h chứng minh AHMK là hình chữ nhật
Sửa đề: ΔABC vuông tại A
Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{HAK}=90^0\)
=>AHMK là hình chữ nhật
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A; M là trung điểm của BC ; Lấy E sao cho M là trung điểm của AE a: Chứng minh ABEC là hcn b: Lấy E sao cho B là trung điểm của AE . Gọi I là trung điểm của BE ; Chứng minh rằng IC=Ì
Sửa đề: Lấy F sao cho B là trung điểm của AF
a: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
nên ABEC là hình bình hành
Hình bình hành ABEC có \(\widehat{BAC}=90^0\)
nên ABEC là hình chữ nhật
b: ABEC là hình chữ nhật
=>AB//EC và AB=EC
AB=EC
BA=BF
Do đó: BF=EC
Xét tứ giác BFEC có
BF//EC
BF=EC
Do đó: BFEC là hình bình hành
=>BE cắt FC tại trung điểm của mỗi đường
mà I là trung điểm của BE
nên I là trung điểm của FC
=>IF=IC
Đúng 1
Bình luận (0)