Bài 9: Hình chữ nhật
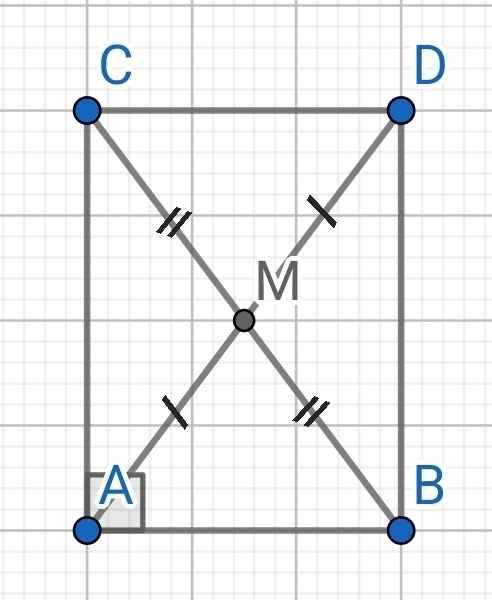a) Do AM là đường trung tuyến của ∆ABC
⇒ M là trung điểm BC
Do MA = MD (gt)
⇒ M là trung điểm AD
Tứ giác ABDC có:
M là trung điểm BC (cmt)
M là trung điểm AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (gt)
⇒ ABDC là hình chữ nhật
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC
⇒ AM = BC : 2
= 10 : 2
= 5 (cm)
c) Nếu ∠B = 45⁰
⇒ C = 90⁰ - ∠B
= 90⁰ - 45⁰
= 45⁰
⇒ ∆ABC vuông cân tại A
⇒ AB = AC
Lại có ABDC là hình chữ nhật
⇒ ABDC là hình vuông
Đúng 0
Bình luận (0)
giúp t bài này với cảm ơn mn trc ạ
Câu 1:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>BC=10(cm)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=5\left(cm\right)\)
c: Xét ΔABC vuông tại A có \(\widehat{ABC}=45^0\)
nên ΔABC vuông cân tại A
=>AB=AC
Hình chữ nhật ABDC có AB=AC
nên ABDC là hình vuông
Câu 2:
a: Xét tứ giác MEKH có
G là trung điểm chung của MK và EH
=>MEKH là hình bình hành
Hình bình hành MEKH có \(\widehat{MHK}=90^0\)
nên MEKH là hình chữ nhật
b: Xét ΔMHK có
N,G lần lượt là trung điểm của MH,MK
=>NG là đường trung bình của ΔMHK
=>NG//HK và NG=HK/2
NG//HK
\(D\in HK\)
Do đó: NG//HD
\(NG=\dfrac{HK}{2}\)
\(HD=\dfrac{HK}{2}\)
Do đó: NG=HD
Xét tứ giác NGDH có
NG//DH
NG=DH
Do đó: NGDH là hình bình hành
Hình bình hành NGDH có \(\widehat{NHD}=90^0\)
nên NGDH là hình chữ nhật
Đúng 0
Bình luận (0)
Câu 1:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>BC=10(cm)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=5\left(cm\right)\)
c: Xét ΔABC vuông tại A có \(\widehat{ABC}=45^0\)
nên ΔABC vuông cân tại A
=>AB=AC
Hình chữ nhật ABDC có AB=AC
nên ABDC là hình vuông
Câu 2:
a: Xét tứ giác MEKH có
G là trung điểm chung của MK và EH
=>MEKH là hình bình hành
Hình bình hành MEKH có \(\widehat{MHK}=90^0\)
nên MEKH là hình chữ nhật
b: Xét ΔMHK có
N,G lần lượt là trung điểm của MH,MK
=>NG là đường trung bình của ΔMHK
=>NG//HK và NG=HK/2
NG//HK
\(D\in HK\)
Do đó: NG//HD
\(NG=\dfrac{HK}{2}\)
\(HD=\dfrac{HK}{2}\)
Do đó: NG=HD
Xét tứ giác NGDH có
NG//DH
NG=DH
Do đó: NGDH là hình bình hành
Hình bình hành NGDH có \(\widehat{NHD}=90^0\)
nên NGDH là hình chữ nhật
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD, lấy điểm E trong hình chữ nhật sao cho EA:EB:EC = 1:2:3. Tính giá trị góc AEB
cho tam giác abc vuông tại a. Có đươngf cao AH. gọi p,q là hình chiếu cảu H xuống ab,ac. I là trùng điểm của bh, k là trung điểm của hc, ah cắt pq tại o
a) tứ giác aphq là hình j?
b)cm tam giác kqh là tam giác cân
c)cm kqp=90 độ và pi//qk
a: Xét tứ giác APHQ có
góc APH=góc AQH=góc PAQ=90 độ
=>APHQ là hình chữ nhật
b: ΔCQH vuông tại Q
mà QK là trung tuyến
nên KQ=KH=KC
=>ΔKQH cân tại K
c: góc KQP=góc KQH+góc PQH
=góc KHQ+góc PAH
=góc HAB+góc HBA=90 độ
góc QPI=góc QPH+góc IPH
=góc QAH+góc IHP
=góc HAC+góc HCA=90 độ
=>QP vuông góc PI
mà QP vuông góc QK
nên QK//PI
Đúng 0
Bình luận (0)
Bài 5. Cho hình chữ nhật ABCD. Nối C với một điểm E bất kì trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại H và K. Chứng minh:
a) Tứ giác AHFK là hình chữ nhật
b) AF // BD;
c) Ba điểm E, H, K thẳng hàng.
a: Xét tứ giác AHFK có
góc AHF=góc AKF=góc KAH=90 độ
=>AHFK là hình chữ nhật
b: Gọi O là giao của AC và BD, I là giao của AF và HK
AHFK là hình chữ nhật
=>I là trung điểm chung của AF và HK
ABCD là hình chữ nhật
=>O là trung điểm chung của AC và BD
Xét ΔAFC có I,O lần lượt là trung điểm của AF,AC
=>IO là đường trung bình
=>IO//FC và IO=FC/2
=>IO//FE và IO=FE
Xét tứ giác IFEO có
IO//FE
IO=FE
=>IFEO là hình bình hành
=>IF//OE
=>AF//BD
Đúng 1
Bình luận (0)
Bài 6. Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM và AB, K là giao điểm của EM và AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng,
b) Tứ giác IAKM là hình chữ nhật
c) Tam giác DME là tam giác vuông cân.
a: góc DAE=góc DAB+góc BAC+góc EAC
=45+90+45=180 độ
=>D,A,E thẳng hàng
b: ΔABC vuông tại A có AM là trung tuyến
nên MA=MB=MC
MA=MB
DA=DB
=>MD là trung trực của AB
=>MD vuông góc AB tại I
MA=MC
EA=EC
=>ME là trung trực của AC
=>ME vuông góc AC tại K
Xét tứ giác AIMK có
góc AIM=góc AKM=góc KAI=90 độ
=>AIMK là hình chữ nhật
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AH là đường cao , đường trung tuyến AM . qua H kẻ đường thẳng song song với AB và AC ,lần lượt cắt AC ở P và AB ở D . DP cắt AH ở O và AM ở Q
a)chứng minh AH=DP
b) tam giác MAC là tam giác j ? Vì sao ?
C)chứng minh tam giác APQ vuông ở Q
a: Xét tứ giác ADHP có
AD//HP
AP//HD
góc PAD=90 độ
Do đó: ADHP là hình chữ nhật
=>AH=DP
b: ΔABC vuông tại A có AM là đường trung tuyến
nên MA=1/2BC=MC=MB
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
c: góc QAP+góc QPA
=góc MAC+góc APD
=góc MCA+góc AHD
=góc ACB+góc ABC=90 độ
=>ΔQAP vuông tại Q
Đúng 5
Bình luận (0)
Bài 2. Cho tam giác ABC vuông tại A. Một đường thẳng song song với BC cắt hai cạnh AB vàAC lần lượt tại D và E. Gọi M và N lần lượt là trung điểm của DE và BC. Chứng minh rằng:a) Ba điểm A, M, N thẳng hàng;b) MN 2BC DEBài 3. Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HE AB; HF AC. Từ A vẽ mộtđường thẳng vuông góc với EF cắt BC tại M. Chứng minh rằng M là trung điểm của BC.
Đọc tiếp
Bài 2. Cho tam giác ABC vuông tại A. Một đường thẳng song song với BC cắt hai cạnh AB và
AC lần lượt tại D và E. Gọi M và N lần lượt là trung điểm của DE và BC. Chứng minh rằng:
a) Ba điểm A, M, N thẳng hàng;
b) MN =
2
BC DE
Bài 3. Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HE AB; HF AC. Từ A vẽ một
đường thẳng vuông góc với EF cắt BC tại M. Chứng minh rằng M là trung điểm của BC.
3:
Xét tứ giác AEHF có
góc AEH=góc AFH=góc EAF=90 độ
=>AEHF là hình chữ nhật
AM vuông góc EF
=>góc MAC+góc AFE=90 độ
=>góc MAC+góc AHE=90 độ
=>góc MAC+góc B=90 độ
mà góc MCA+góc B=90 độ
nên góc MAC=góc MCA
=>MA=MC
góc MAC+góc MAB=90 độ
góc MCA+góc MBA=90 độ
mà góc MAC=góc MCA
nên góc MAB=góc MBA
=>MA=MB
=>MB=MC
=>M là trung điểm của BC
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông cân tại C trên cạnh AC BC lấy lần lượt lấy các điểm P Q sao cho Ac = CD từ điểm B vẽ BM song song với BC M thuộc AB Chứng minh pcqm là hình chữ nhật(vẽ luôn hình aa)
Để chứng minh PCQM là hình chữ nhật, ta cần chứng minh 4 đỉnh P,, Q, M đều thuộc một đường thẳng và đường thẳng đó vuông góc với cả hai đường PQ và CM.Ta sẽ chứng minh từng bước như sau:Bước 1: Chứng minh P, C, Q thẳng hàngVì tam giác ABC vuông cân tại C và BM song song với BC, nên theo thuộc tính tam giác vuông cân và tam giác đồng dạng:- Ta có AC = BC (tam giác vuông cân)- Ta có BM || BC (theo giả thiết)- Ta có ∠ABC = ∠BAC (tam giác vuông cân)Do đó, tam giác ABC đồng dạng với tam giác BPC (theo góc). Từ đó, ta có:∠BPC = ∠ACB = 90° - ∠ABC = 90° - ∠BAC = ∠BCA (do tam giác vuông cân)Vậy ta có P, C,
Đúng 0
Bình luận (0)