Bài 12: Hình vuông
Nội dung lý thuyết
Các phiên bản khác1. Định nghĩa
Cho hình vẽ:
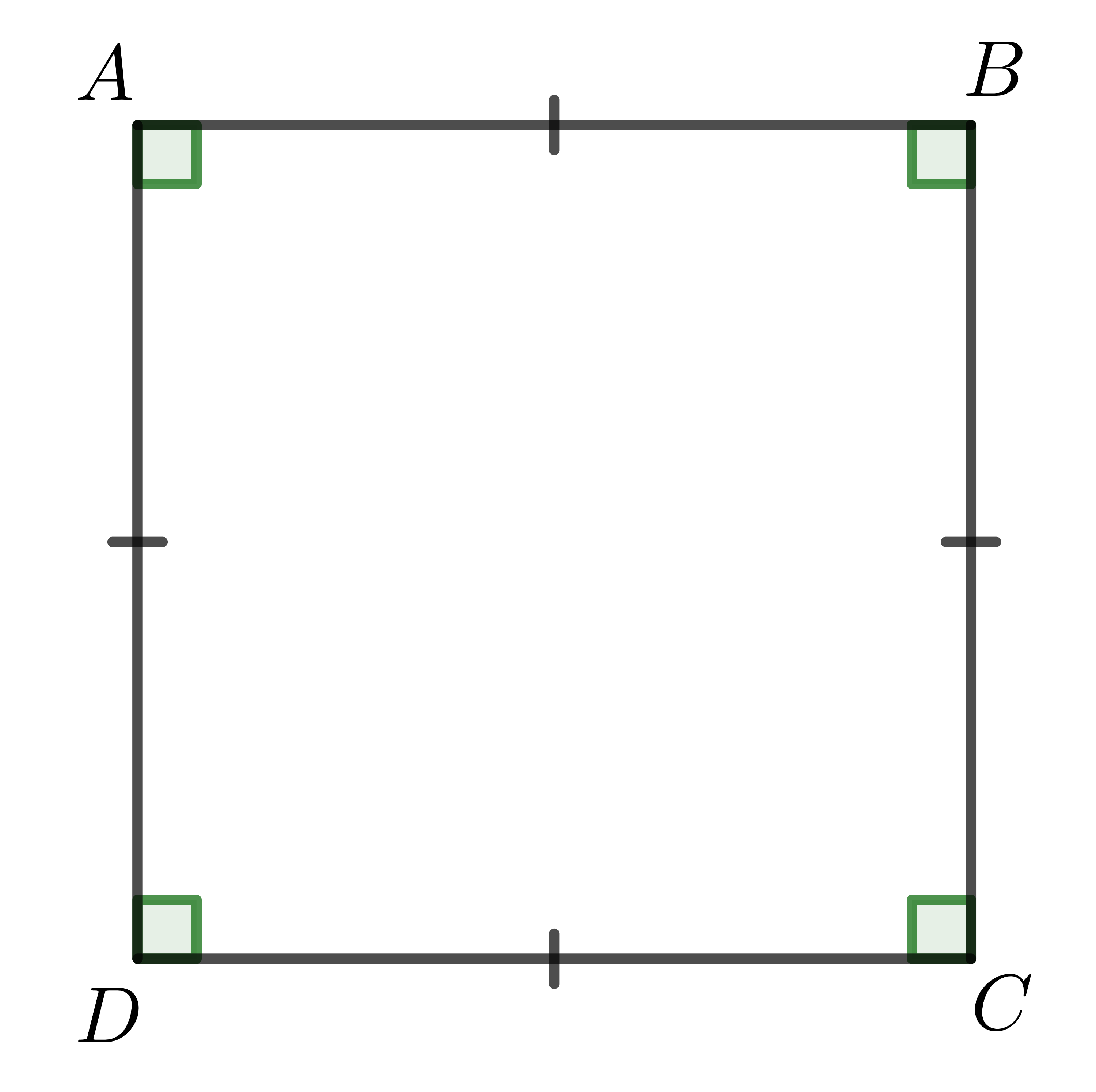
Trong hình trên, tứ giác \(ABCD\) có \(AB=BC=CD=AD\) và \(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\). Ta gọi \(ABCD\) là một hình vuông.
Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Tứ giác \(ABCD\) là hình vuông \(\Leftrightarrow\left\{{}\begin{matrix}AB=BC=CD=AD\\\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\end{matrix}\right.\).
Từ định nghĩa, ta suy ra:
- Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
- Hình vuông là hình thoi có bốn góc vuông.
Nhận xét: Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
2. Tính chất
Ở trên ta đã biết, hình vuông vừa là hình thoi vừa là hình chữ nhật, do đó nó có tất cả các tính chất của hình thoi và hình chữ nhật:
- Các cạnh bằng nhau, các góc bằng nhau (theo định nghĩa).
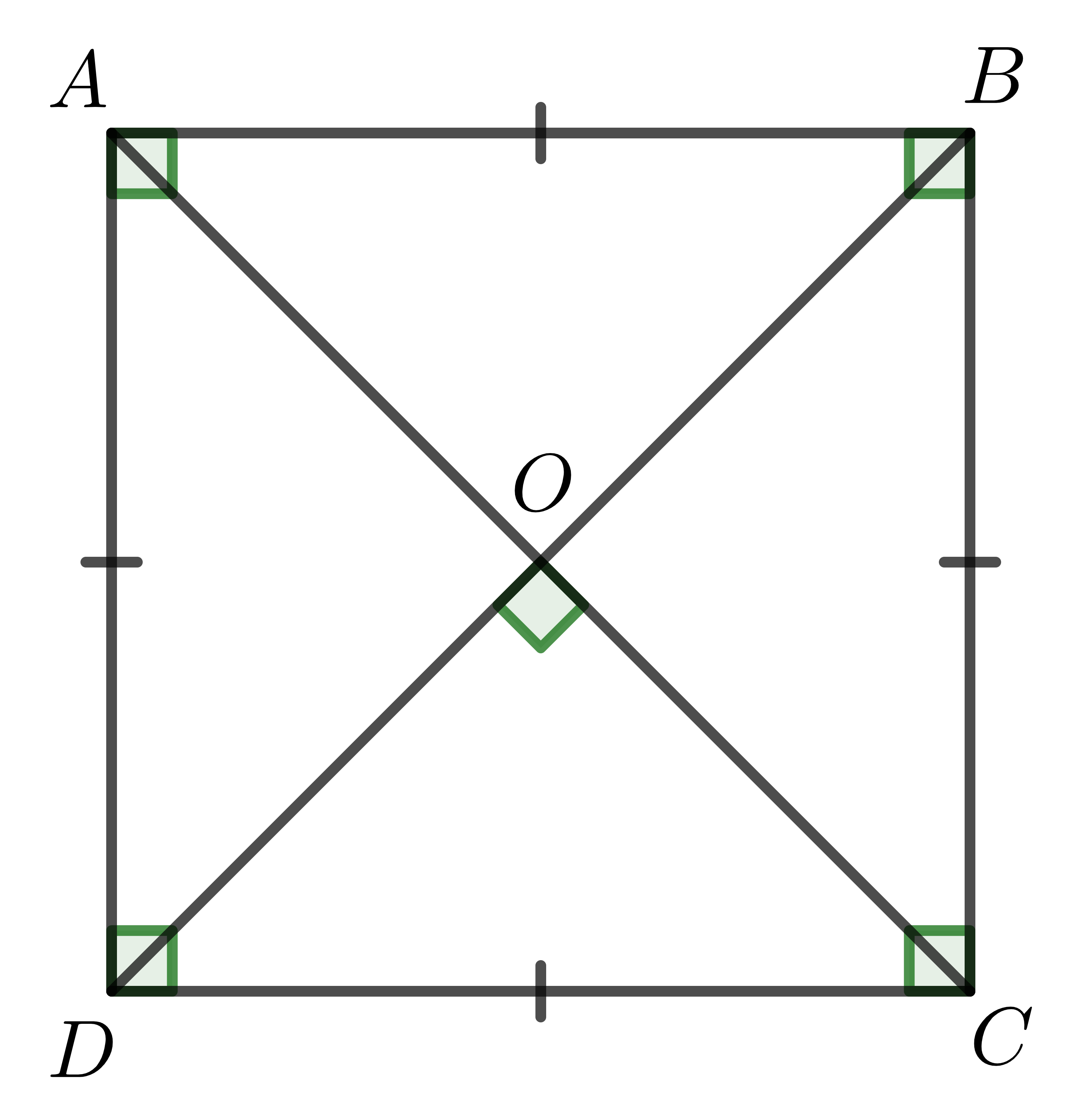
- Hai đường chéo bằng nhau và vuông góc với nhau tại trung điểm mỗi đường.
3. Dấu hiệu nhận biết
Ta có thể nhận biết một tứ giác là hình vuông dựa vào các dấu hiệu sau:
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
- Hình chữ nhật có một đường chéo là phân giác của một góc là hình vuông.
- Hình thoi có một góc vuông là hình vuông.
- Hình thoi có hai đường chéo bằng nhau là hình vuông.
Chứng minh:
1. Giả sử \(ABCD\) là hình chữ nhật có \(AB=BC\).
Theo tính chất hình chữ nhật, ta có \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\) mà \(AB=BC\) \(\Rightarrow AB=BC=CD=AD\).
Ta cũng có \(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\) (tính chất hình chữ nhật).
Theo định nghĩa, ta có \(ABCD\) là hình vuông.
2. Xét hình chữ nhật \(ABCD\). Giả sử \(AC\perp BD\equiv O\).
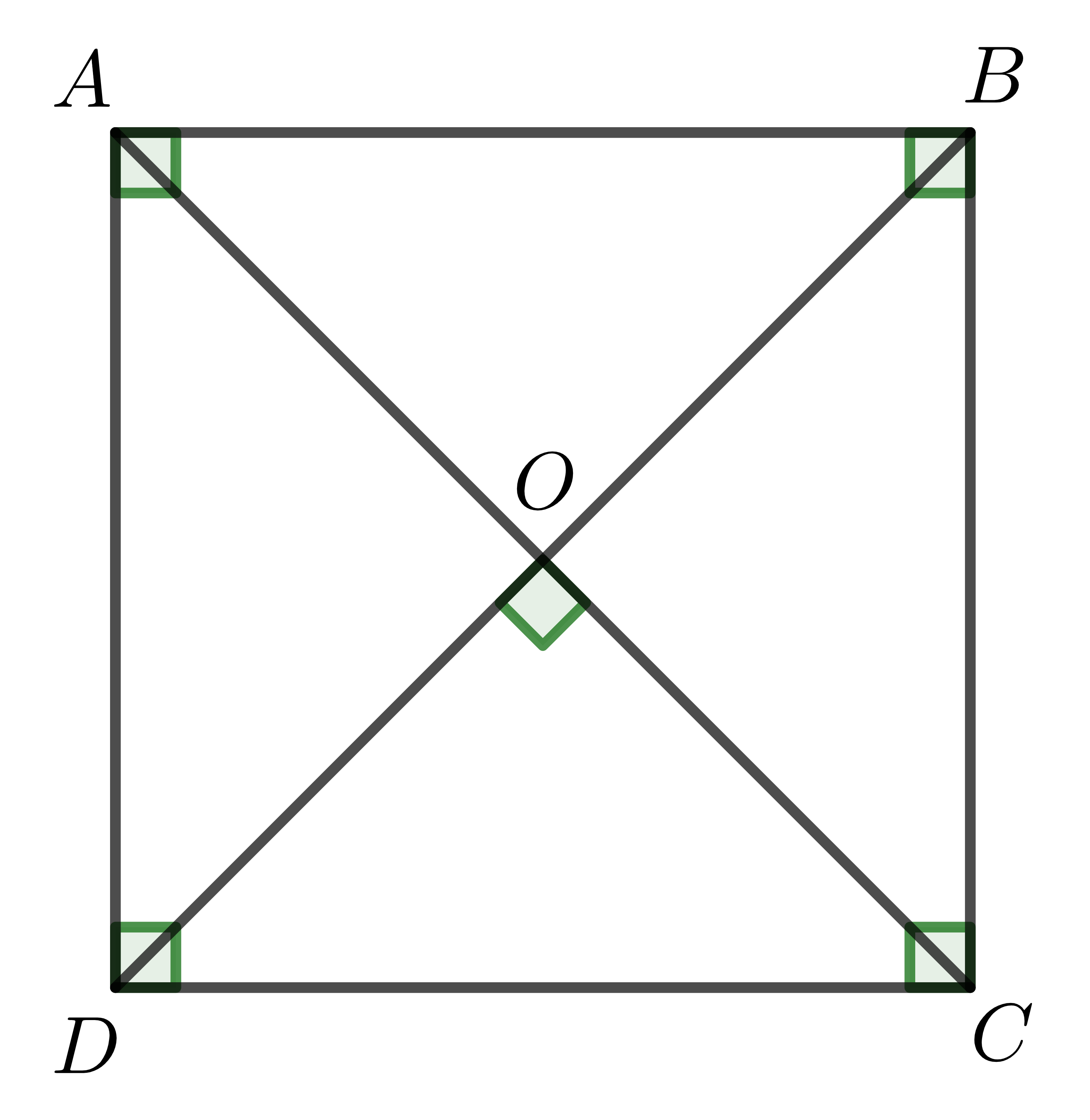
Do \(ABCD\) là hình chữ nhật nên \(O\) là trung điểm \(AC,BD\) nên \(AO\) là trung tuyến của tam giác \(ABD\).
Theo giả thiết, \(AO\perp BD\) nên \(AO\) là đường cao của tam giác \(ABD\).
\(\Rightarrow\Delta ABD\) cân tại \(A\Rightarrow AB=AD\).
Theo dấu hiệu 1, ta suy ra \(ABCD\) là hình vuông.
3. Xét hình chữ nhật \(ABCD\), \(AC\) là phân giác góc \(A\).
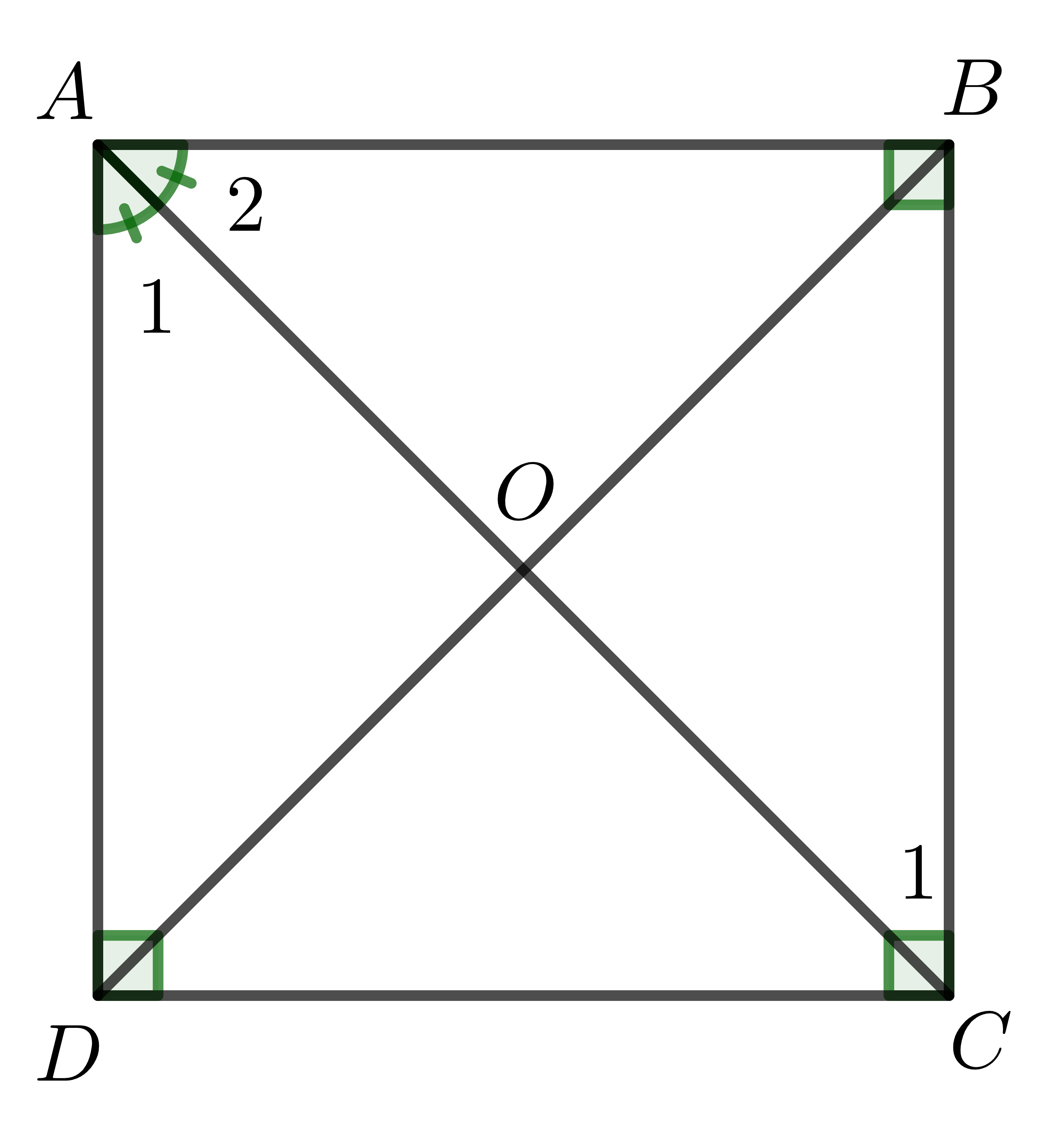
Do \(\widehat{A}=90^0\Rightarrow\widehat{A_1}=\widehat{A_2}=45^0\).
Theo tính chất hình chữ nhật, ta có \(AD\)//\(BC\) \(\Rightarrow\widehat{A_1}=\widehat{C_1}=45^0\) (hai góc so le trong).
\(\Rightarrow\widehat{A_2}=\widehat{C_1}=45^0\Rightarrow\Delta BAC\) vuông cân \(\Rightarrow AB=BC\).
Theo dấu hiệu 1, ta có \(ABCD\) là hình vuông.
4. Xét hình thoi \(ABCD\) có \(\widehat{A}=90^0\).
Theo tính chất hình thoi ta có \(\left\{{}\begin{matrix}AB=BC=CD=AD\\\widehat{A}=\widehat{C}=90^0;\widehat{B}=\widehat{D}\\\widehat{A}+\widehat{B}=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AB=BC=CD=AD\\\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\end{matrix}\right.\Rightarrow ABCD\) là hình vuông.
5. Xét hình thoi \(ABCD\) có \(AC=BD\).
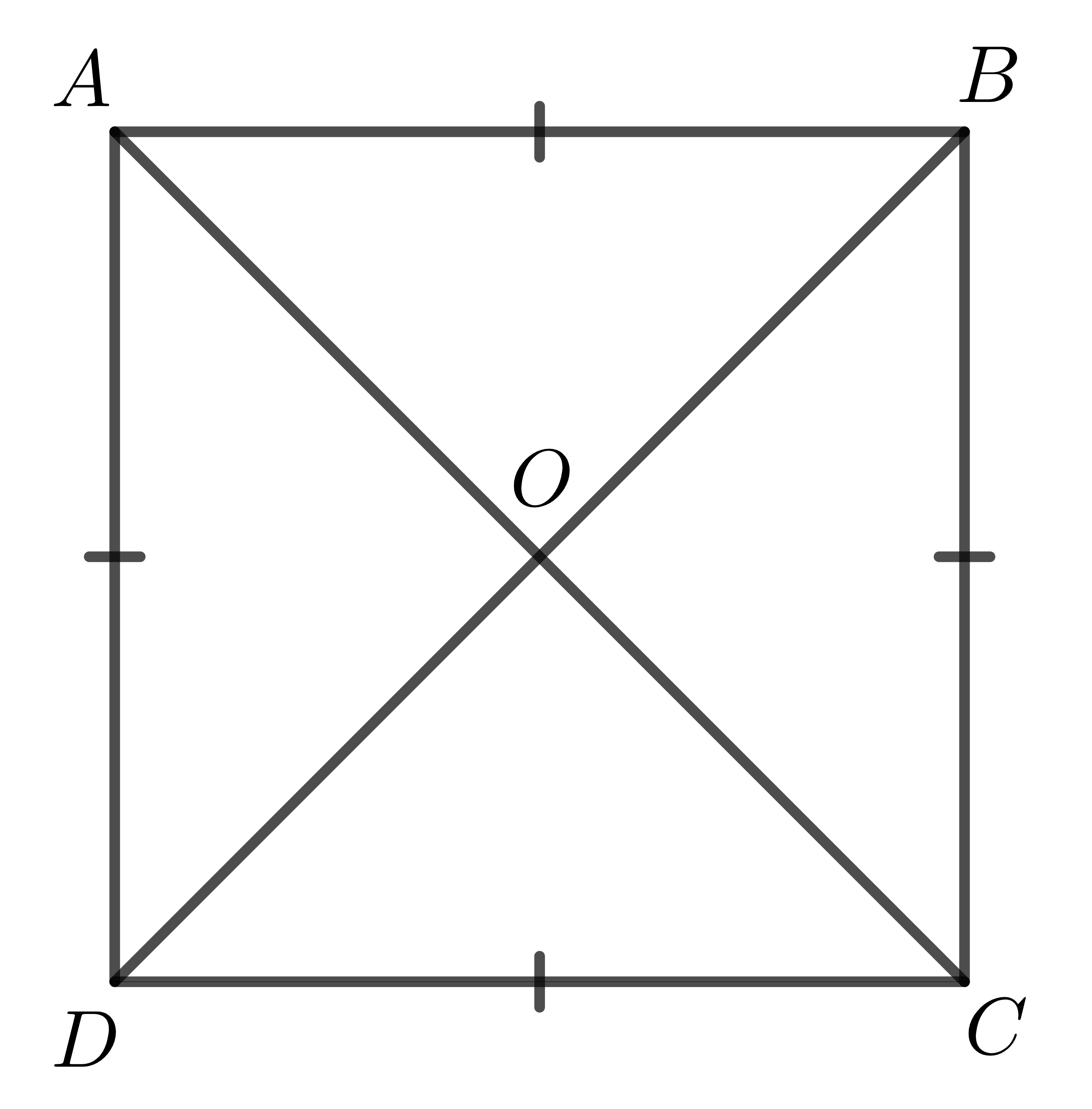
Giả sử \(AC\cap BD\equiv O\). Theo tính chất hình thoi, ta có \(O\) là trung điểm \(AC,BD\).
Mà \(AC=BD\Rightarrow OA=OB=OC=OD\).
Tam giác \(ABC\) có \(BO\) là trung tuyến ứng với \(AC\) và \(BO=\dfrac{1}{2}AC\) \(\Rightarrow\Delta ABC\) vuông.
Theo dấu hiệu 4, ta có \(ABCD\) là hình vuông.
Như vậy, trong thực hành, ta cần sử dụng linh hoạt một trong các dấu hiệu trên để chứng minh một tứ giác là hình vuông.
Ví dụ: Cho tam giác \(ABC\) vuông cân tại \(A\). Gọi \(M,N,P\) lần lượt là trung điểm \(AB,BC,AC\). Chứng minh tứ giác \(AMNP\) là hình vuông.
Lời giải:
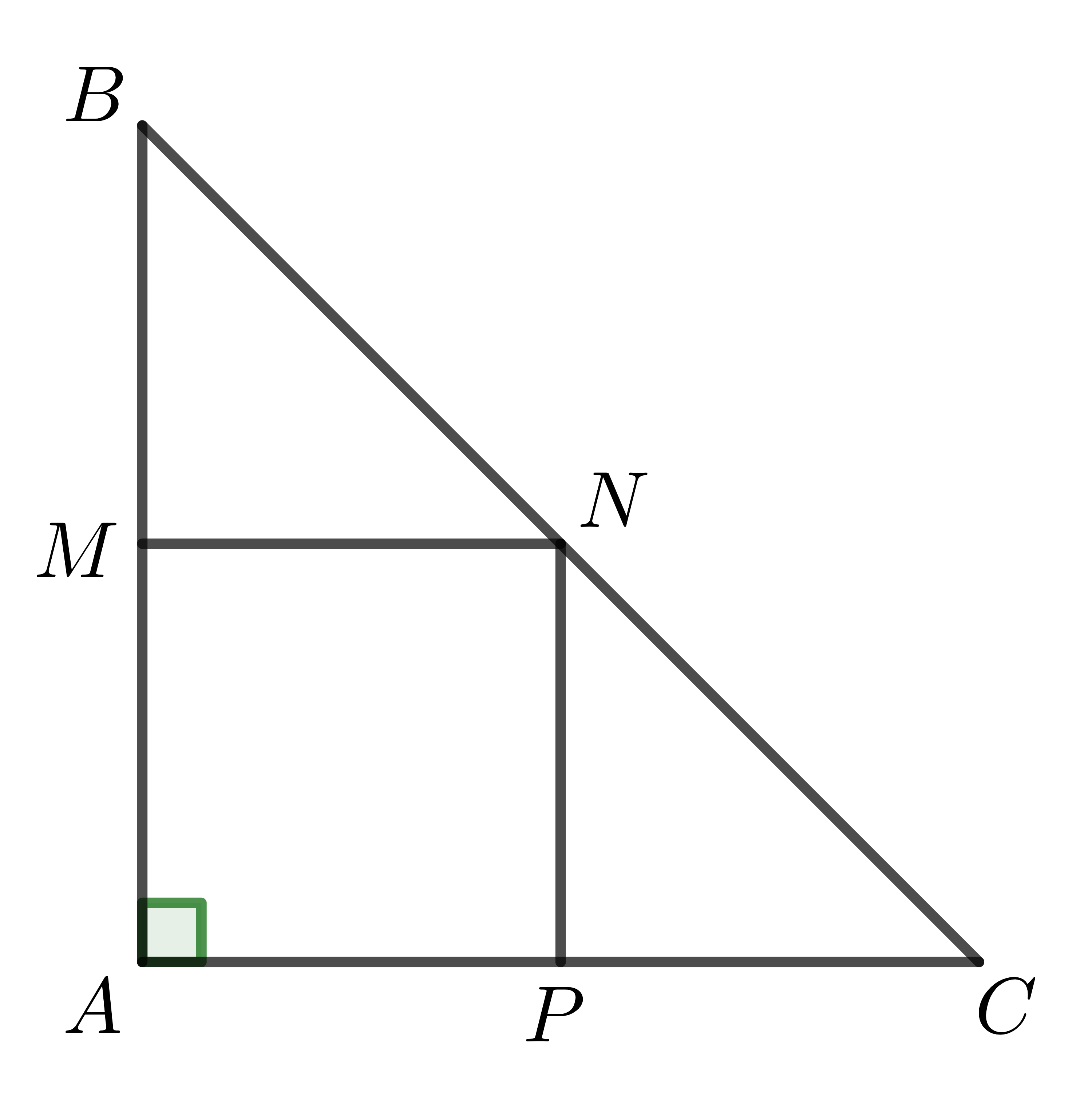
Do \(M,N,P\) lần lượt là trung điểm \(AB,BC,AC\) nên \(MN,NP\) lần lượt là đường trung bình ứng với các cạnh \(AC,AB\).
\(\Rightarrow\left\{{}\begin{matrix}AM=NP=\dfrac{1}{2}AB\\AP=MN=\dfrac{1}{2}AC\end{matrix}\right.\) mà \(AB=AC\) (do tam giác \(ABC\) cân tại \(A\))
\(\Rightarrow AM=MN=NP=AP\). Do đó \(AMNP\) là hình thoi.
Lại có \(\widehat{A}=90^0\) (do tam giác \(ABC\) vuông tại \(A\)).
Theo dấu hiệu 4, ta suy ra \(AMNP\) là hình vuông.
@621386@