Bài 5: Dựng hình bằng thước và compa. Dựng hình thang
Nội dung lý thuyết
Các phiên bản khác1. Bài toán dựng hình
Ta đã biết vẽ hình bằng nhiều dụng cụ: thước, compa, êke.... Ta xét các bài toán vẽ hình mà chỉ sử dụng hai dụng cụ là thước và compa, chúng được gọi là các bài toán dựng hình.
Với thước, ta có thể:
Vẽ được một đường thẳng khi biết hai điểm của nó.
Vẽ được một đoạn thẳng khi biết hai đầu mút của nó.
Vẽ được một tia khi biết gốc và một điểm của tia.
Với compa, ta có thể vẽ được một đường tròn khi biết tâm và bán kính của nó.
2. Các bài toán dựng hình đã biết
Dùng thước và compa, chúng ta đã biết cách giải một số bài toán dựng hình sau:
Dựng một đoạn thẳng bằng một đoạn thẳng cho trước.
Dựng một góc bằng một góc cho trước.
Dựng đường trung trực của một đoạn thẳng cho trước, dựng trung điểm của đoạn thẳng cho trước.
Dựng tia phân giác của một góc cho trước.
Qua một điểm cho trước, dựng đường thẳng vuông góc với một đường thẳng cho trước.
Qua một điểm nằm ngoài một đường thẳng cho trước, dựng đường thẳng song song với một đường thẳng cho trước.
Các dạng dựng tam giác (biết ba cạnh, biết hai cạnh và góc xen giữa, một cạnh và hai góc kề).
Dựng một tam giác đều hoặc một hình vuông khi biết một cạnh của nó.
Dựng hình chữ nhật khi biết hai cạnh kề.
3. Dựng hình thang
Ta hãy nhớ kết quả:
Muốn dựng hình thang, cần biết bốn yếu tố, trong đó số yếu tố về góc không quá 2.
Muốn dựng hình thang cân, cần biết ba yếu tố, trong đó số yếu tố về góc không quá 1.
Ví dụ: Dựng hình thang \(ABCD\) biết đáy \(AB=4cm\), đáy \(CD=5cm\), cạnh bên \(AD=3cm,\widehat{D}=60^0\).


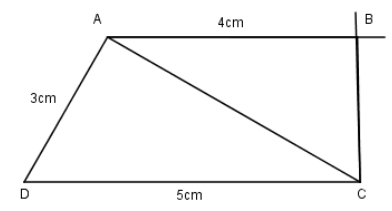
a) Phân tích:
Giả sử đã dựng được hình thang \(ABCD\) thỏa mãn yêu cầu bài toán. Tam giác \(ACD\) dựng được do đã biết hai cạnh và góc xen giữa. Điểm \(B\) phải thỏa mãn hai điều kiện:
- \(B\) nằm trên đường thẳng đi qua \(A\) và song song với \(CD\).
- \(B\) cách \(A\) một khoảng bằng \(4cm\) nên nằm trên đường tròn tâm \(A\) bán kính \(4cm\).
b) Cách dựng:
- Dựng tam giác \(ACD\) có \(\widehat{D}=60^0;AD=3cm;CD=5cm\).
- Dựng tia \(Ax\) song song với \(CD\) (tia \(Ax\) và điểm \(C\) nằm trên cùng một nửa mặt phẳng bờ \(AD\)).
- Dựng điểm \(B\) trên tia \(Ax\) sao cho \(AB=4cm\). Kẻ đoạn thẳng \(BC\).
c) Chứng minh:
Tứ giác \(ABCD\) là hình thang vì \(AB\)//\(CD\).
Ta có \(CD=5cm;AD=3cm;AB=4cm;\widehat{D}=60^0\) nên hình thang \(ABCD\) vừa dựng thỏa mãn yêu cầu bài toán.
d) Biện luận:
Ta luôn dựng được hình thang thỏa mãn yêu cầu đề bài.