Bài 9: Hình chữ nhật

a: Xét tứ giác ADME có

\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)

=>ADME là hình chữ nhật

b; XétΔABC có

M là trung điểm của BC

MD//AC

Do đó: D là trung điểm của AB

Xét ΔABC có

M là trung điểm của BC

ME//AB

Do đó: E là trung điểm của AC

ΔABC vuông tại A có AM là trung tuyến

nên AM=BC/2=BM=CM

Xét tứ giác AMBI có

D là trung điểm chung của AB và MI

Do đó: AMBI là hình bình hành

mà MA=MB

nên AMBI là hình thoi

c: Để AMBI là hình vuông thì \(\widehat{AMB}=90^0\)

=>AM\(\perp\)BC

Xét ΔABC có

AM là đường cao, là đường trung tuyến

Do đó: ΔABC cân tại A

=>AB=AC

a: Xét tứ giác AEDF có

\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)

=>AEDF là hình chữ nhật

=>AD cắt EF tại trung điểm của mỗi đường

mà I là trung điểm của EF

nên I là trung điểm của AD

=>A,I,D thẳng hàng

b: Xét ΔBAC có DE//AC

nên \(\dfrac{DE}{AC}=\dfrac{BD}{BC}\)

Xét ΔBAC có DF//AB

nên \(\dfrac{DF}{AB}=\dfrac{CD}{CB}\)

\(\dfrac{DE}{AC}+\dfrac{DF}{AB}=\dfrac{BD}{BC}+\dfrac{CD}{BC}=1\)

=>\(\dfrac{DE}{AB}+\dfrac{DF}{AB}=1\)

=>\(DE+DF=AB\)

=>\(2\cdot\left(DE+DF\right)=2AB\)

=>\(C_{AEDF}=2\cdot AB\) không đổi

CHÚC EM HỌC TỐT NHÁ

a: Xét tứ giác AHCD có

M là trung điểm chung của AC và HD

\(\widehat{AHC}=90^0\)

Do đó: AHCD là hình chữ nhật

b: ΔABC cân tại A

mà AH là đường cao

nên H là trung điểm của BC

Xét ΔABC có

H,M lần lượt là trung điểm của CB,CA

=>HM làđường trung bình

=>HM//AB và HM=AB/2

mà HM=HD/2

nên AB=HD

c: 

AHCD là hình bình hành

=>AD//CH và AD=CH

AD//CH

=>AD//BH

AD=CH

CH=BH

Do đó: AD=BH

Xét tứ giác ABHD có 

AD//BH

AD=BH

Do đó: ABHD là hình bình hành

Bài 1:

a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có

AD=CB

\(\widehat{ADH}=\widehat{CBK}\)

Do đó: ΔAHD=ΔCKB

=>AH=CK

AH\(\perp\)BD

CK\(\perp\)BD

Do đó: AH//CK

Xét tứ giác AHCK có

AH//CK

AH=CK

Do đó: AHCK là hình bình hành

b: AHCK là hình bình hành

=>AK//CH

mà \(M\in AK;N\in HC\)

nên AM//CN

Xét tứ giác AMCN có

AM//CN

AN//CM

Do đó: AMCN là hình bình hành

=>AN=CM 

c: AMCN là hình bình hành

=>AM=CN

AK+KM=AM

CH+HN=CN

mà AK=CH(AHCK là hình bình hành)

và AM=CN

nên KM=HN

Xét tứ giác KMHN có

KM//HN

KM=HN

Do đó:KMHN là hình bình hành

=>KH cắt MN tại trung điểm của mỗi đường

mà O là trung điểm của HK

nên O là trung điểm của MN

=>M,O,N thẳng hàng

Bài 3: 

a: Xét tứ giác ADME có

\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)

=>ADME là hình chữ nhật

=>AM=DE

b: ADME là hình chữ nhật

=>AM cắt DE tại trung điểm của mỗi đường

mà I là trung điểm của DE

nên I là trung điểm của AM

ΔHAM vuông tại H

mà HI là đường trung tuyến

nên IH=IA=IM

IH=IA

=>I nằm trên đường trung trực của AH

Còn ai thức ko

a: Xét tứ giác AHCE có

I là trung điểm chung của AC và HE

=>AHCE là hình bình hành

Hình bình hành AHCE có \(\widehat{AHC}=90^0\)

nên AHCE là hình chữ nhật

b: Xét ΔAHC có

HI,AM là đường trung tuyến

HI cắt AM tại G

Do đó: G là trọng tâm của ΔAHC

=>\(HG=\dfrac{2}{3}HI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot HE=\dfrac{1}{3}HE\)

Xét ΔEAC có

AN,EI là đường trung tuyến

AN cắt EI tại K

Do đó: K là trọng tâm của ΔEAC

=>\(EK=\dfrac{2}{3}EI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot EH=\dfrac{1}{3}EH\)

HG+GK+KE=HE

=>\(GK+\dfrac{1}{3}HE+\dfrac{1}{3}HE=HE\)

=>\(GK=HE\left(1-\dfrac{1}{3}-\dfrac{1}{3}\right)=\dfrac{1}{3}HE\)

=>HG=GK=KE

Bài 1

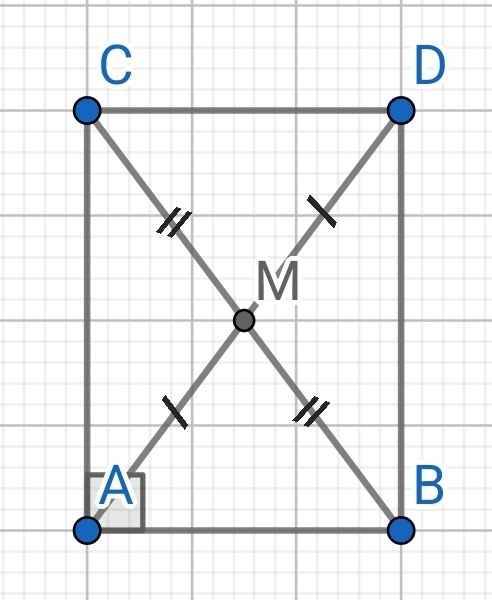 a) Do AM là đường trung tuyến của ∆ABC

⇒ M là trung điểm BC

Do MA = MD (gt)

⇒ M là trung điểm AD

Tứ giác ABDC có:

M là trung điểm BC (cmt)

M là trung điểm AD (cmt)

⇒ ABDC là hình bình hành

Mà ∠BAC = 90⁰ (gt)

⇒ ABDC là hình chữ nhật

b) ∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC

⇒ AM = BC : 2

= 10 : 2

= 5 (cm)

c) Nếu ∠B = 45⁰

⇒ C = 90⁰ - ∠B

= 90⁰ - 45⁰

= 45⁰

⇒ ∆ABC vuông cân tại A

⇒ AB = AC

Lại có ABDC là hình chữ nhật

⇒ ABDC là hình vuông

Bài 2

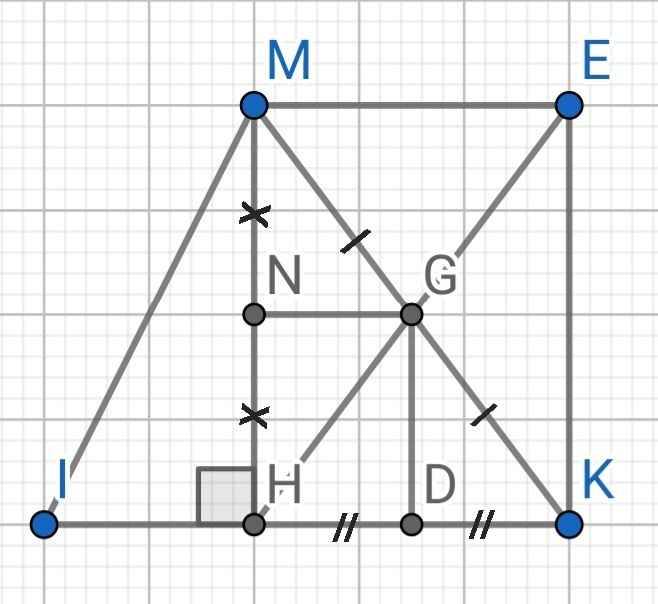a) Do H và E đối xứng với nhau qua G (gt)

⇒ G là trung điểm của HE

Tứ giác MEKH có:

G là trung điểm HE (cmt)

G là trung điểm MK (gt)

⇒ MEKH là hình bình hành

Mà ∠MHK = 90⁰ (MH ⊥ IK)

⇒ MEKH là hình chữ nhật

b) ∆MHK có:

N là trung điểm MH (gt)

G là trung điểm MK (gt)

⇒ NG là đường trung bình của ∆MHK

⇒ NG // HK và NG = HK : 2

Do D là trung điểm HK

⇒ HD = HK : 2

⇒ HD = NG = HK : 2

Do NG // HK

⇒ NG // HD

Do ∠MHK = 90⁰

⇒ ∠NHD = 90⁰

Tứ giác NGDH có:

NG // HD (cmt)

NG = HD (cmt)

⇒ NGDH là hình bình hành

Mà ∠NHD = 90⁰ (cmt)

⇒ NGDH là hình chữ nhật

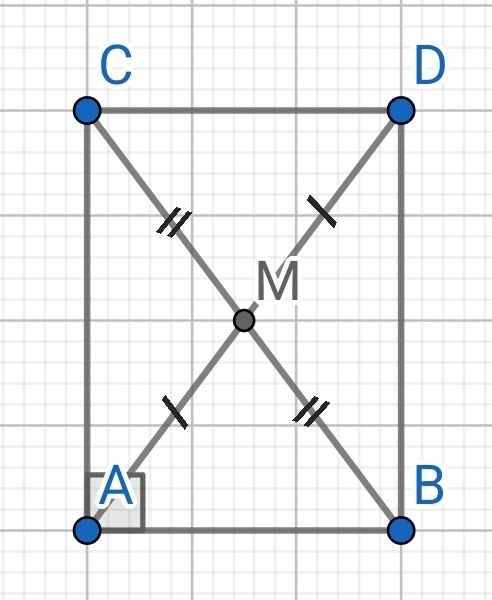
a) Do AM là đường trung tuyến của ∆ABC

⇒ M là trung điểm BC

Do MA = MD (gt)

⇒ M là trung điểm AD

Tứ giác ABDC có:

M là trung điểm BC (cmt)

M là trung điểm AD (cmt)

⇒ ABDC là hình bình hành

Mà ∠BAC = 90⁰ (gt)

⇒ ABDC là hình chữ nhật

b) ∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC

⇒ AM = BC : 2

= 10 : 2

= 5 (cm)

c) Nếu ∠B = 45⁰

⇒ C = 90⁰ - ∠B

= 90⁰ - 45⁰

= 45⁰

⇒ ∆ABC vuông cân tại A

⇒ AB = AC

Lại có ABDC là hình chữ nhật

⇒ ABDC là hình vuông