Question

Answer 1

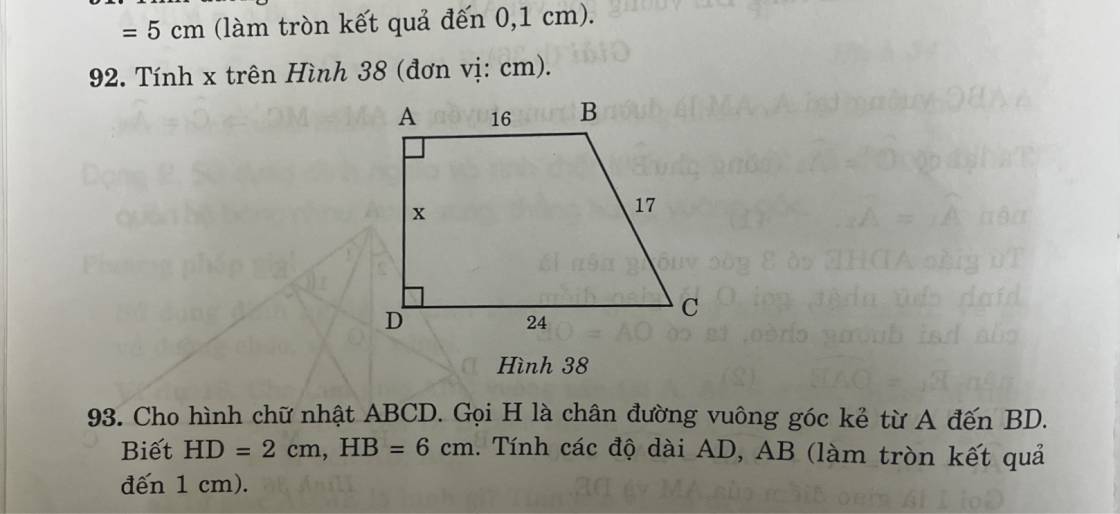
92:

Kẻ BH\(\perp\)DC tại H

Xét tứ giác ABHD có

\(\widehat{BHD}=\widehat{BAD}=\widehat{ADH}=90^0\)

=>ABHD là hình chữ nhật

=>AB=HD=16cm

HD+HC=CD

=>HC+16=24

=>HC=8cm

ΔBHC vuông tại H

=>\(BH^2+HC^2=BC^2\)

=>\(BH^2+8^2=17^2\)

=>\(BH^2+64=289\)

=>\(BH^2=225\)

=>BH=15(cm)

ABHD là hình chữ nhật

=>AD=BH=15(cm)

=>x=15(cm)

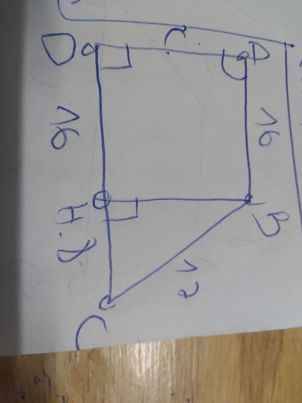
93:

BD=BH+DH

=6+2

=8(cm)

Xét ΔABD vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BD\\AD^2=DH\cdot DB\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}AB^2=6\cdot8=48\\AD^2=2\cdot8=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=4\sqrt{3}\left(cm\right)\\AD=4\left(cm\right)\end{matrix}\right.\)