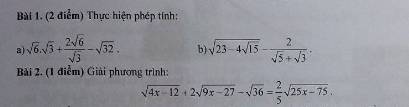Bài 8: Rút gọn biểu thức chứa căn bậc hai
Gọi số bài đạt điểm khá và số bài đạt điểm giỏi trong tháng 9 lần lượt là a,b
Tổng số bài đạt điểm khá giỏi trong tháng 9 là 30 bài nên ta có:
a+b=30
Trong tháng 10, số bài đạt điểm giỏi tăng 20% và số bài đạt điểm khá giảm 30% nên tổng số bài đạt điểm khá giỏi là 26 bài nên ta có:
1,2a+0,7b=26
Do đó, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=30\\1.2a+0.7b=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1.2a+1.2b=36\\1.2a+0.7b=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0.5b=10\\a+b=30\end{matrix}\right.\)
=>b=20 và a=10
Đúng 2
Bình luận (0)
Gọi số bài đạt điểm giỏi và điểm khá của lớp 9A lần lược là: \(a,b\left(a,b\in N\right)\)
Tổng số bài trong tháng 9 là 30 \(\Rightarrow a+b=30\left(1\right)\)
Trong tháng 10 điểm giỏi tăng 20% và điểm khá giảm 30% nên tổng số là 26 ta có:
\(\left(1+0,2\right)a+\left(1-0,3\right)b=1,2a+0,7b=26\) (2)
Từ (1) và (2) ta có hệ pt:
\(\left\{{}\begin{matrix}a+b=30\\1,2a+0,7b=26\end{matrix}\right.\) giải hệ ta có:
\(\Leftrightarrow\left\{{}\begin{matrix}a=10\\b=20\end{matrix}\right.\left(tm\right)\)
Vậy: ...
Đúng 3
Bình luận (0)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AC^2=CH\cdot CB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=\dfrac{8\cdot6}{10}=4.8\left(cm\right)\\CH=\dfrac{6^2}{10}=3.6\left(cm\right)\end{matrix}\right.\)
HD=AH/2=2,4cm
ΔCHD vuông tại H
=>\(CD^2=CH^2+HD^2\)
=>\(CD=\sqrt{3.6^2+2.4^2}=\dfrac{6}{5}\sqrt{13}\left(cm\right)\)
Đúng 3
Bình luận (0)
Bài 1:
a) \(\sqrt{6}\cdot\sqrt{3}+\dfrac{2\sqrt{6}}{\sqrt{3}}-\sqrt{32}\)
\(=\sqrt{3}\cdot\sqrt{2}\cdot\sqrt{3}+\dfrac{2\cdot\sqrt{3}\cdot\sqrt{2}}{\sqrt{3}}-\sqrt{4^2\cdot2}\)
\(=3\sqrt{2}+2\sqrt{2}-4\sqrt{2}\)
\(=\left(3+2-4\right)\sqrt{2}\)
\(=\sqrt{2}\)
b) \(\sqrt{23-4\sqrt{15}}-\dfrac{2}{\sqrt{5}+\sqrt{3}}\)
\(=\sqrt{\left(2\sqrt{5}\right)^2-2\cdot2\sqrt{5}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}-\dfrac{2\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}\)
\(=\sqrt{\left(2\sqrt{5}-\sqrt{3}\right)^2}-\dfrac{2\left(\sqrt{5}-\sqrt{3}\right)}{2}\)
\(=2\sqrt{5}-\sqrt{3}-\sqrt{5}+\sqrt{3}\)
\(=\sqrt{5}\)
Đúng 2
Bình luận (0)
2:
ĐKXĐ: x>=3
\(\sqrt{4x-12}+2\sqrt{9x-27}-\sqrt{36}=\dfrac{2}{5}\sqrt{25x-75}\)
=>\(2\sqrt{x-3}+6\sqrt{x-3}-\dfrac{2}{5}\cdot5\sqrt{x-3}=6\)
=>\(6\sqrt{x-3}=6\)
=>x-3=1
=>x=4
Đúng 0
Bình luận (0)
3 căn x trừ căn x bằng bnhieu ạ:))?
Lời giải:
$3\sqrt{x}-\sqrt{x}=2\sqrt{x}$
Đúng 0
Bình luận (0)
Hiệu của 3 căn bậc hai của x trừ đi căn bậc hai của x là:
3√x - √x = (3 - 1)√x = 2√x.
Vậy, hiệu của 3 căn bậc hai của x trừ đi căn bậc hai của x là 2√x.
Đúng 0
Bình luận (0)
Cho P = \(\dfrac{4\sqrt{x}}{4\sqrt{x}+8}\)
So sánh P và |P|
\(P=\dfrac{4\sqrt{x}}{4\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+2}>=0\)
=>P=|P|
Đúng 0
Bình luận (0)
Ta có : \(P=\dfrac{4\sqrt{x}}{4\sqrt{x}+8}\left(x\ge0\right)\)
\(P=\dfrac{4\sqrt{x}}{4.(\sqrt{x}+2)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
Vì : \(\sqrt{x}\ge0;\sqrt{x}+2\ge2\)
\(\Rightarrow P\ge0\)
Do đó : \(P=\left|P\right|\) ( vì cả hai đều dương )
Đúng 0
Bình luận (0)
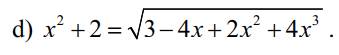
Giải phương trình
\(PT\Leftrightarrow x^4+4x^2+4=4x^3+2x^2-4x+3\)
=>\(x^4-4x^3+2x^2+4x+1=0\)
\(\Leftrightarrow\left(x^2-2x-1\right)^2=0\)
=>x^2-2x-1=0
=>\(x=1\pm\sqrt{2}\)
Đúng 0
Bình luận (0)
\(x^2+2=\sqrt{3-4x+2x^2+4x^3}\)
\(\Leftrightarrow\left(x^2+2\right)^2=4x^3+2x^2-4x+3\)
\(\Leftrightarrow\left(x^2\right)^2+2\cdot2\cdot x^2+2^2=4x^3+2x^2-4x+3\)
\(\Leftrightarrow x^4+4x^2+4=4x^3+2x^2-4x+3\)
\(\Leftrightarrow x^4-4x^3+\left(4x^2-2x^2\right)+4x+\left(4-3\right)=0\)
\(\Leftrightarrow x^4-4x^3+2x^2+4x+1=0\)
\(\Leftrightarrow\left(x^2-2x-1\right)^2=0\)
\(\Leftrightarrow x^2-2x-1=0\)
\(\Rightarrow\Delta=\left(-2\right)^2-4\cdot1\cdot-1=8>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{2+2\sqrt{2}}{2}=1+\sqrt{2}\\x_2=\dfrac{2-2\sqrt{2}}{2}=1-\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow x=1\pm\sqrt{2}\)
Đúng 0
Bình luận (0)
Để giải phương trình x^2 + 2 = √3 - 4x + 2x^2 + 4x^3, chúng ta cần tìm giá trị của x thỏa mãn phương trình này. Dưới đây là quá trình giải phương trình:
1. Đưa tất cả các thuật ngữ chứa x về cùng một bên của phương trình và để hệ số của x^3 là dương:
4x^3 + 2x^2 + 4x + x^2 + 4x - √3 + 2 = 0
2. Kết hợp các thuật ngữ tương tự:
4x^3 + 3x^2 + 8x - √3 + 2 = 0
3. Giải phương trình này không dễ dàng bằng cách sử dụng phép tính truyền thống. Thay vào đó, chúng ta có thể tìm nghiệm gần đúng bằng phương pháp số học hoặc sử dụng máy tính.
Kết quả gần đúng cho x là khoảng x ≈ 0.287106. Để tìm nghiệm chính xác, bạn có thể sử dụng phần mềm máy tính hoặc phương pháp giải đa thức bậc ba nếu cần.
Đúng 0
Bình luận (0)
Cho P= \(\dfrac{x}{\sqrt{x}-1}\) , x > 1.Tìm GTNN của P
Ta có:
\(P=\dfrac{x}{\sqrt{x}-1}=\dfrac{x-4\sqrt{x}+4+4\sqrt{x}-4}{\sqrt{x}-1}\)
\(P=\dfrac{\left(x-4\sqrt{x}+4\right)+4\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}+4\)
Mà: \(x>1\Rightarrow\sqrt{x}-1>0\Rightarrow\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}\ge0\forall x\)
\(\Rightarrow P=\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}+4\ge4\forall x\)
Dấu "=" xảy ra:
\(\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}+4=4\)
\(\Leftrightarrow\sqrt{x}-2=0\)
\(\Leftrightarrow\sqrt{x}=2\)
\(\Leftrightarrow x=4\)
Vậy: \(P_{min}=4\Leftrightarrow x=4\)
Đúng 1
Bình luận (0)
\(P=\dfrac{x}{\sqrt[]{x}-1}\left(x>1\right)\)
\(\Leftrightarrow P=\dfrac{x-1+1}{\sqrt[]{x}-1}\)
\(\Leftrightarrow P=\dfrac{\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}+1\right)+1}{\sqrt[]{x}-1}\)
\(\Leftrightarrow P=\sqrt[]{x}+1+\dfrac{1}{\sqrt[]{x}-1}\)
\(\Leftrightarrow P=\sqrt[]{x}-1+\dfrac{1}{\sqrt[]{x}-1}+2\)
Áp dụng BĐT Cauchy cho 2 số dương \(\sqrt[]{x}-1;\dfrac{1}{\sqrt[]{x}-1}\)
\(P=\sqrt[]{x}-1+\dfrac{1}{\sqrt[]{x}-1}+2\ge2+2=4\)
Dấu "=" xảy ra khi và chỉ khi
\(\sqrt[]{x}-1=\dfrac{1}{\sqrt[]{x}-1}\)
\(\Leftrightarrow\left(\sqrt[]{x}-1\right)^2=1\)
\(\Leftrightarrow\sqrt[]{x}-1=1\left(x>1\Rightarrow\sqrt[]{x}-1>0\right)\)
\(\Leftrightarrow\sqrt[]{x}=2\)
\(\Leftrightarrow x=4\)
Vậy \(GTNN\left(P\right)=4\left(khi.x=4\right)\)
Đúng 1
Bình luận (0)
\(P=\left(\dfrac{1-a\sqrt{a}}{1-a}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2\) (ĐK: \(a\ge0;a\ne1\))
\(P=\left[\dfrac{1^3-\left(\sqrt{a}\right)^3}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}+\sqrt{a}\right]\cdot\dfrac{\left(1-\sqrt{a}\right)^2}{\left(1-a\right)^2}\)
\(P=\left[\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}+\sqrt{a}\right]\cdot\dfrac{\left(1-\sqrt{a}\right)^2}{\left(1-\sqrt{a}\right)^2\left(1+\sqrt{a}\right)^2}\)
\(P=\left[\dfrac{1+\sqrt{a}+a}{\sqrt{a}+1}+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\cdot\dfrac{1}{\left(1+\sqrt{a}\right)^2}\)
\(P=\dfrac{1+\sqrt{a}+a+a+\sqrt{a}}{\sqrt{a}+1}\cdot\dfrac{1}{\left(1+\sqrt{a}\right)^2}\)
\(P=\dfrac{2a+2\sqrt{a}+1}{\sqrt{a}+1}\cdot\dfrac{1}{\left(\sqrt{a}+1\right)^2}\)
\(P=\dfrac{2a+2\sqrt{a}+1}{\left(\sqrt{a}+1\right)^3}\)
Đúng 0
Bình luận (0)
\(a,A=\dfrac{\sqrt{x}+3}{x-4}\left(x\ge0;x\ne4\right)\)
Thay \(x=9\) vào \(A\), ta được:
\(A=\dfrac{\sqrt{9}+3}{9-4}=\dfrac{3+3}{5}=\dfrac{6}{5}\)
\(---\)
\(b,B=\dfrac{-4}{x-4}+\dfrac{1}{\sqrt{x}-2}\left(x\ge0;x\ne4\right)\)
\(=\dfrac{-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{-4+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{1}{\sqrt{x}+2}\)
\(---\)
\(c,P=\dfrac{A}{B}\left(x>4\right)\)
\(=\dfrac{\sqrt{x}+3}{x-4}:\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2+5}{\sqrt{x}-2}\)
\(=1+\dfrac{5}{\sqrt{x}-2}\)
Khi đó: \(x>4\Leftrightarrow\sqrt{x}>2\)
\(\Leftrightarrow\sqrt{x}-2>0\)
\(\Leftrightarrow\dfrac{5}{\sqrt{x}-2}>0\)
\(\Leftrightarrow1+\dfrac{5}{\sqrt{x}-2}>1\)
hay \(P>1\) khi \(x>4\)
#\(Toru\)
Đúng 1
Bình luận (0)