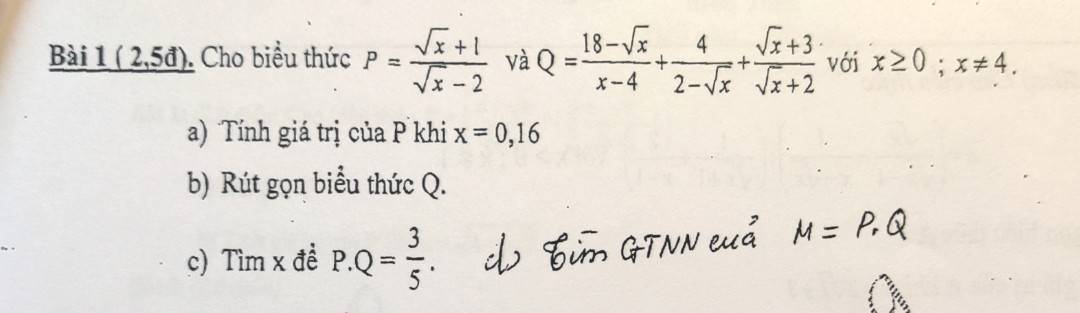Bài 8: Rút gọn biểu thức chứa căn bậc hai
a: Xét ΔABO vuông tại B có \(cosBOA=\dfrac{BO}{OA}=\dfrac{R}{2R}=\dfrac{1}{2}\)
nên \(\widehat{BOA}=60^0\)
b: ΔOBC cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}\)
=>\(\widehat{OCA}=90^0\)
c: Gọi I là giao điểm của CO với BD
Ta có: BD//AC
OC\(\perp\)AC
Do đó: OC\(\perp\)BD tại I
=>OI là khoảng cách từ O xuống BD
OC\(\perp\)CA
=>OC là khoảng cách từ O xuống AC
Vì BD//AC và I,O,C thẳng hàng
nên khoảng cách từ BD đến AC sẽ là khoảng cách từ I đến C
=>Khoảng cách từ BD đến AC là IC
Ta có: ΔBOA=ΔCOA
=>\(\widehat{BOA}=\widehat{COA}\)
=>\(\widehat{COA}=60^0\)
Ta có: \(\widehat{ACH}+\widehat{CAH}=90^0\)(ΔACH vuông tại H)
\(\widehat{OCA}+\widehat{OAC}=90^0\)(ΔOCA vuông tại C)
Do đó: \(\widehat{ACH}=\widehat{OCA}=60^0\)
BD//AC
=>\(\widehat{DBC}=\widehat{BCA}\)(hai góc so le trong)
=>\(\widehat{DBC}=60^0\)
\(\widehat{BOC}=\widehat{BOA}+\widehat{COA}=60^0+60^0=120^0\)
Xét (O) có \(\widehat{BDC}\) là góc nội tiếp chắn cung BC
nên \(\widehat{BDC}=\dfrac{\widehat{BOC}}{2}=\dfrac{120^0}{2}=60^0\)
Xét ΔBDC có \(\widehat{BDC}=\widehat{DBC}=60^0\)
nên ΔBDC đều
Ta có: ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
Xét ΔBOA vuông tại B có BH là đường cao
nên \(BH\cdot OA=BO\cdot BA\)
=>\(BH=\dfrac{R\cdot R\sqrt{3}}{2R}=\dfrac{R\sqrt{3}}{2}\)
ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>\(BC=2\cdot BH=R\sqrt{3}\)
Xét ΔBDC đều có CI là đường cao
nên \(CI=BC\cdot\dfrac{\sqrt{3}}{2}=R\sqrt{3}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3R}{2}\)
=>Khoảng cách từ dây AC đến dây BD là 3R/2
Đúng 1
Bình luận (1)
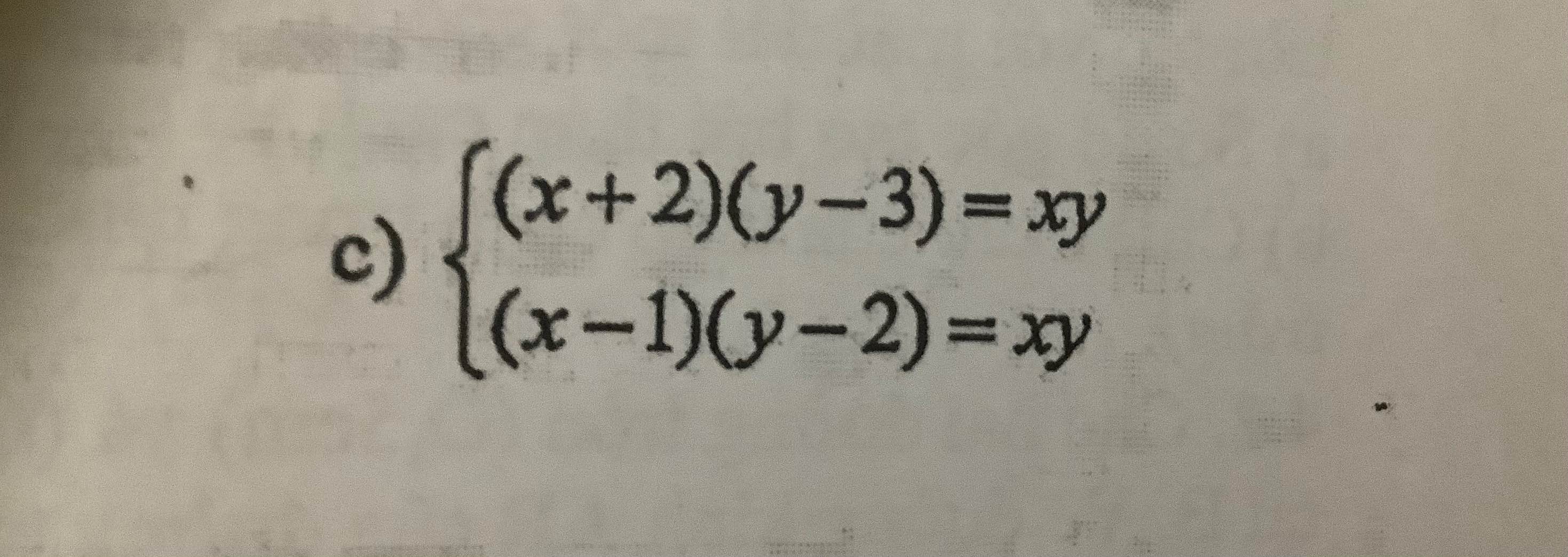 giúp mình với ạaaaaaa
giúp mình với ạaaaaaa
Ta có: \(\left\{{}\begin{matrix}\left(x+2\right)\left(y-3\right)=xy\\\left(x-1\right)\left(y-2\right)=xy\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}xy-3x+2y-6=xy\\xy-2x-y+2=xy\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x+2y=6\\-2x-y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x+2y=6\\-4x-2y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x+2y-4x-2y=6-4\\2x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-7x=2\\y=2-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{7}\\y=2-2\cdot\dfrac{-2}{7}=2+\dfrac{4}{7}=\dfrac{18}{7}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
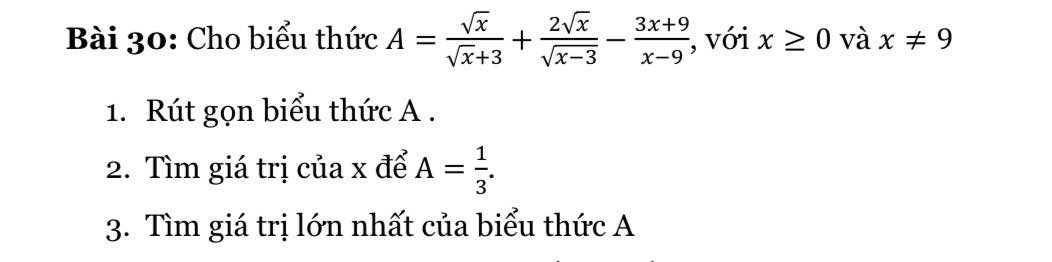 hộ mình câu c) với ạaa
hộ mình câu c) với ạaa
1: \(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3}{\sqrt{x}+3}\)
2: \(A=\dfrac{1}{3}\)
=>\(\dfrac{3}{\sqrt{x}+3}=\dfrac{1}{3}\)
=>\(\sqrt{x}+3=3\cdot3=9\)
=>\(\sqrt{x}=9-3=6\)
=>x=36(nhận)
3: \(\sqrt{x}+3>=3\forall x\) thỏa mãn ĐKXĐ
=>\(A=\dfrac{3}{\sqrt{x}+3}< =\dfrac{3}{3}=1\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x=0
Đúng 1
Bình luận (0)
Tính
- (- sqrt(123)) ^ 2
= ????
\(-\left(-\sqrt{123}\right)^2=-123\)
Đúng 1
Bình luận (1)
Giúp em bài này với ạ
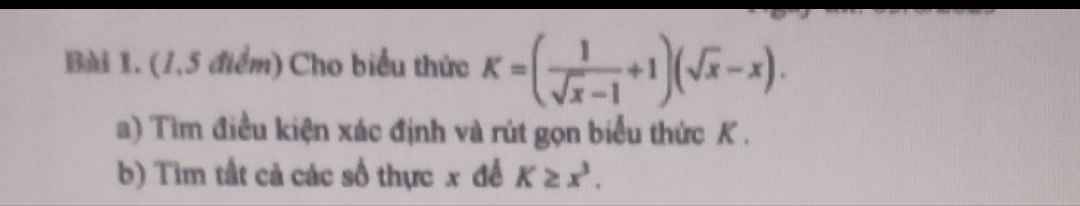
Mà câu a như vậy đúng không ạ 💀💔
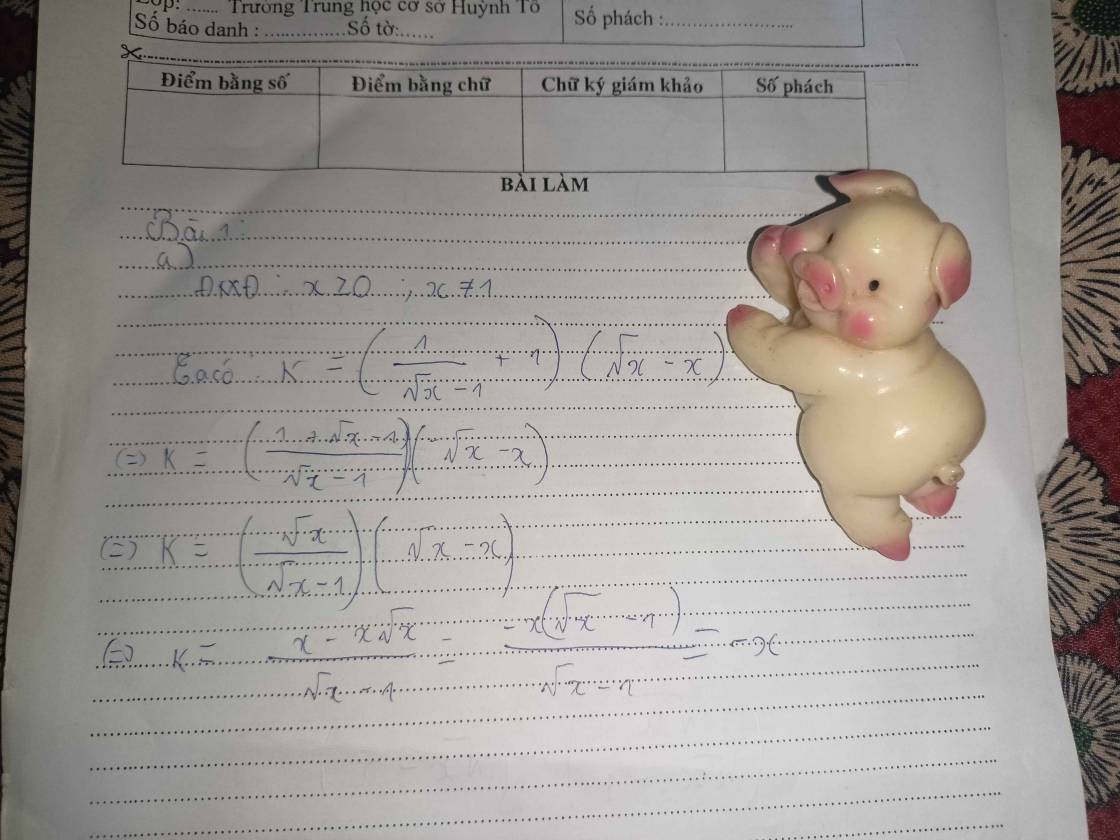
b.
\(K\ge x^3\) \(\Leftrightarrow-x\ge x^3\)
\(\Leftrightarrow x^3+x\le0\)
\(\Leftrightarrow x\left(x^2+1\right)\le0\)
\(\Leftrightarrow x\le0\) (do \(x^2+1>0;\forall x\))
Kết hợp ĐKXĐ \(x\ge0\)
\(\Rightarrow x=0\)
Đúng 2
Bình luận (0)
Câu a đúng nha
b) Giả sử: x thỏa mãn \(K\ge x^3\) là \(x\le0\)
(1) : x=0
\(< =>-0=0^3\)
\(< =>0=0\)(Luôn đúng)
(2):x<0
\(< =>-\left(-x\right)>\left(-x\right)^3\)
\(< =>x>\left(-x\right)^3\)( Luôn đúng do \(\left(-x\right)^3\) luôn âm)
(1)(2) => Để thỏa mãn \(K\ge x^3\) thì \(x\le0\)
Đúng 1
Bình luận (1)
1) Giải hệ phương trình: (x - 1)(y + 1) = xy - 1; (x - 2)(y - 2) = xy - 8
\(\left\{{}\begin{matrix}\left(x-1\right)\left(y+1\right)=xy-1\\\left(x-2\right)\left(y-2\right)=xy-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}xy+x-y-1=xy-1\\xy-2x-2y+4=xy-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y=0\\-2x-2y=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-2y=0\\2x+2y=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=12\\x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=x=3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(\left\{{}\begin{matrix}\left(x-1\right)\left(y+1\right)=xy-1\\\left(x-2\right)\left(y-2\right)=xy-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy+x-y-1=xy-1\\xy-2x-2y+4=xy-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\x+y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Truyện ngắn Làng của Kim Lân đã thể hiện một cáchchân thực sâu sắc và cảm động tình yêu làng quê và lòngyêu nước, tinh thần kháng chiến của người nông dânphải rời làng đi tản cư.Hãy phân tích diễn biến tâm trạng nhân vật ông Hai đểam sảng tỏ nhận định trên bằng một đoạn tổng- phân-hợp. Đoạn văn có sử dụng câu bị động và thành phầnphụ chú.
Đọc tiếp
Truyện ngắn Làng của Kim Lân đã thể hiện một cách
chân thực sâu sắc và cảm động tình yêu làng quê và lòng
yêu nước, tinh thần kháng chiến của người nông dân
phải rời làng đi tản cư.
Hãy phân tích diễn biến tâm trạng nhân vật ông Hai để
am sảng tỏ nhận định trên bằng một đoạn tổng- phân-
hợp. Đoạn văn có sử dụng câu bị động và thành phần
phụ chú.
ai giúp mik trả lời đc câu hỏi đc ko ạ
Đúng 0
Bình luận (0)
Bài 1 (2,0 điểm) Cho A = (x * sqrt(x) + 1)/(x + 2sqrt(x) + 1) * v * dB = (2x + 6sqrt(x) + 7)/(x * sqrt(x) + 1) - 1/(sqrt(x) + 1) * v * dix >= 0
a) Rút gọn A và tính giá trị của A khi x = 4
b) Rút gọn M = A B. Tm * d\&M>2
c) Tìm x để M là số nguyên
a: \(A=\dfrac{x\sqrt{x}+1}{x+2\sqrt{x}+1}\)
ĐKXĐ: x>=0
\(A=\dfrac{x\sqrt{x}+1}{x+2\sqrt{x}+1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\)
Thay x=4 vào A, ta được:
\(A=\dfrac{4-2+1}{2+1}=\dfrac{5-2}{3}=1\)
b: M=A*B
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\cdot\left(\dfrac{2x+6\sqrt{x}+7}{x\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right)\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\cdot\left(\dfrac{2x+6\sqrt{x}+7}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}+1}\right)\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\cdot\dfrac{2x+6\sqrt{x}+7-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\cdot\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}+1\right)^2}=\dfrac{\sqrt{x}+6}{\sqrt{x}+1}\)
Để M>2 thì M-2>0
=>\(\dfrac{\sqrt{x}+6-2\sqrt{x}-2}{\sqrt{x}+1}>0\)
=>\(-\sqrt{x}+4>0\)
=>\(-\sqrt{x}>-4\)
=>\(\sqrt{x}< 4\)
=>0<=x<16
c: Để M là số nguyên thì \(\sqrt{x}+6⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1+5⋮\sqrt{x}+1\)
=>\(5⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{0;-2;4;-6\right\}\)
=>\(\sqrt{x}\in\left\{0;4\right\}\)
=>\(x\in\left\{0;16\right\}\)
Đúng 1
Bình luận (0)
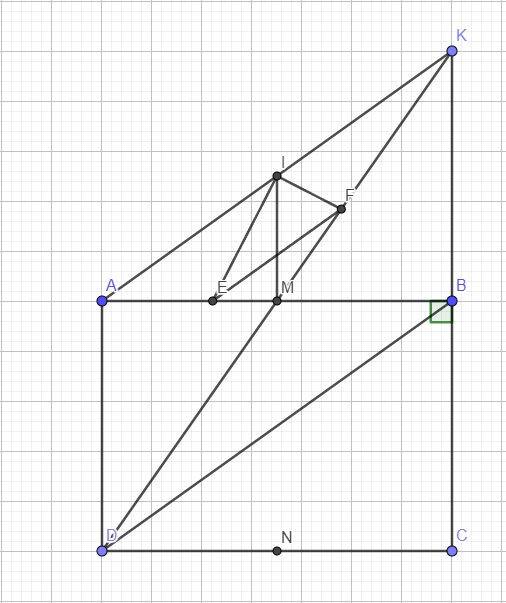
Cho hình chữ nhật ABCD(ABAD), gọi M là trung điểm cạnh AB. Từ M kẻ MN vuông góc với CD tại N( N thuộc CD)a, Trên tia DM lấy điểm K sao cho M là trung điểm của đoạn thẳng DK. Chứng minh tứ giác ADBK là hình bình hành và tam giác AKC cân.b,Gọi I là trung điểm của AK. Tia phân giác của góc AIM cắt AM tại E, tia phân giác của góc KIM cắt MK ở F. Chứng minh EF song song với BD.
Đọc tiếp
Cho hình chữ nhật ABCD(AB>AD), gọi M là trung điểm cạnh AB. Từ M kẻ MN vuông góc với CD tại N( N thuộc CD)
a, Trên tia DM lấy điểm K sao cho M là trung điểm của đoạn thẳng DK. Chứng minh tứ giác ADBK là hình bình hành và tam giác AKC cân.
b,Gọi I là trung điểm của AK. Tia phân giác của góc AIM cắt AM tại E, tia phân giác của góc KIM cắt MK ở F. Chứng minh EF song song với BD.
a.
Xét tứ giác ADBK có: hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường
\(\Rightarrow ADBK\) là hình bình hành
Do ABCD là hình chữ nhật \(\Rightarrow AB\perp BC\Rightarrow AB\) là đường cao tam giác ACK
Theo cmt, ADBK là hbh \(\Rightarrow BK=AD\)
Mà \(AD=BC\) (ABCD là hcn)
\(\Rightarrow BK=BC\Rightarrow AB\) là trung tuyến tam giác ACK
\(\Rightarrow AB\) vừa là đường cao vừa là trung tuyến nên tam giác ACK cân tại A
b.
Do IE là phân giác, áp dụng định lý phân giác trong tam giác IAM:
\(\dfrac{EM}{EA}=\dfrac{IM}{IA}\) (1)
Do IF là phân giác, áp dụng định lý phân giác trong tam giác IMK:
\(\dfrac{FM}{FK}=\dfrac{IM}{IK}\) (2)
Mà I là trung điểm AK \(\Rightarrow IA=IK\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{EM}{EA}=\dfrac{FM}{FK}\Rightarrow EF||AK\) (định lý Talet đảo)
Theo c/m câu a do ADBK là hình bình hành \(\Rightarrow AK||BD\)
\(\Rightarrow EF||BD\)
Đúng 1
Bình luận (0)