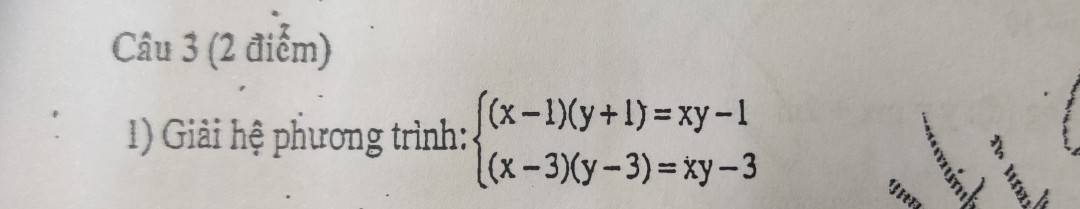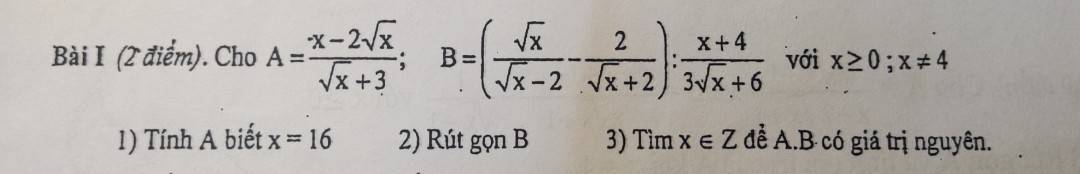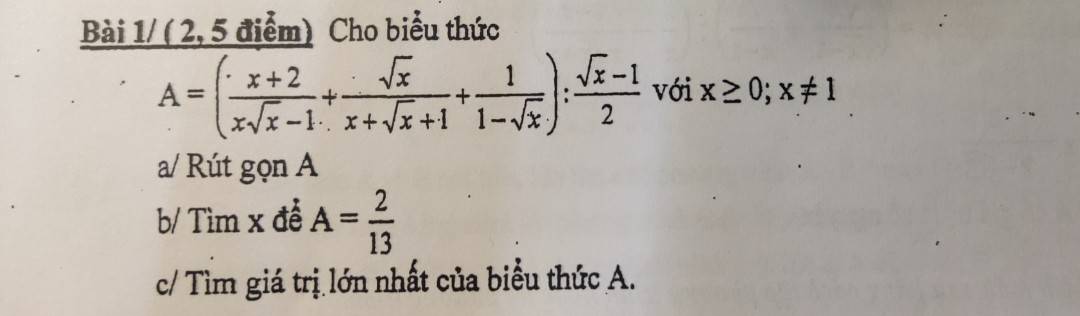
Bài 9: Căn bậc ba

a: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)

\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)

\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)

\(=\dfrac{-\sqrt{x}+1+x-\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+\sqrt{x}+1}\)

b: A=2/13

=>\(x+\sqrt{x}+1=13\)

=>\(x+\sqrt{x}-12=0\)

=>\(\left(\sqrt{x}+4\right)\left(\sqrt{x}-3\right)=0\)

=>\(\sqrt{x}-3=0\)

=>\(\sqrt{x}=3\)

=>x=9(nhận)

c: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=0\cdot1+1=1\forall x\) thỏa mãn ĐKXĐ

=>\(A=\dfrac{2}{x+\sqrt{x}+1}< =\dfrac{2}{1}=2\forall x\) thỏa mãn ĐKXĐ

Dấu '=' xảy ra khi x=0

a) A= \(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)

A= \(\left(\dfrac{x+2}{\sqrt{x^3}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right).\dfrac{2}{\sqrt{x}-1}\)

A= \(\left(\dfrac{x+2+x-\sqrt{x}-x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right).\dfrac{2}{\sqrt{x}-1}\)

A= \(\dfrac{2\left(x+3\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)

\(\left\{{}\begin{matrix}\left(x-1\right)\left(y+1\right)=xy-1\\\left(x-3\right)\left(y-3\right)=xy-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}xy+x-y-1=xy-1\\xy-3x-3y+9=xy-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x-y=0\\-3x-3y=-12\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x-y=0\\x+y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x=4\\x=y\end{matrix}\right.\Leftrightarrow x=y=2\)

1: Thay x=16 vào A, ta được:

\(A=\dfrac{16-2\cdot4}{4+3}=\dfrac{16-8}{7}=\dfrac{8}{7}\)

2: \(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}\right):\dfrac{x+4}{3\sqrt{x}+6}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)-2\cdot\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{3\left(\sqrt{x}+2\right)}{x+4}\)

\(=\dfrac{x+2\sqrt{x}-2\sqrt{x}+4}{\sqrt{x}-2}\cdot\dfrac{3}{x+4}=\dfrac{3}{\sqrt{x}-2}\)

3: Đặt P=A*B

\(=\dfrac{3}{\sqrt{x}-2}\cdot\dfrac{x-2\sqrt{x}}{\sqrt{x}+3}\)

\(=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+3}\)

Để P là số nguyên thì \(3\sqrt{x}⋮\sqrt{x}+3\)

=>\(3\sqrt{x}+9-9⋮\sqrt{x}+3\)

=>\(-9⋮\sqrt{x}+3\)

=>\(\sqrt{x}+3\in\left\{1;-1;3;-3;9;-9\right\}\)

=>\(\sqrt{x}+3\in\left\{3;9\right\}\)

=>\(\sqrt{x}\in\left\{0;6\right\}\)

=>\(x\in\left\{0;36\right\}\)

giải giúp cho mik 1,2,3 đi ạ

ơ ko ai trả lời à

trả lời đi nha,ko có ngồi ì ra thế

em hỏi câu như thế này, không có đoạn văn nào thì trả lời sao em? =))?

trả lời giúp mik với

Tổng 2 vận tốc: 390 : 6 = 65(km/h)

Nếu ô tô khởi hành trước xe máy 3h15p thì ô tô đi từ đầu đến lúc gặp xe máy: 

4 giờ + 3 giờ 15 phút = 7 giờ 15 phút

Nếu ô tô khởi hành trước xe máy 3h15p thì xe máy đi được 4 giờ ít hơn đoạn khoảng thời gian 6 giờ một khoảng là 2 tiếng đồng hồ (8/4 giờ)

Nếu ô tô khởi hành trước xe máy 3h15p thì ô tô đi từ đầu đến lúc gặp xe máy nhiều hơn 6 giờ một khoảng là 1 giờ 15 phút (5/4 giờ)

Vậy quãng đường ô tô đi trong 5/4 giờ = quãng đường xe máy đi trong 2 giờ

Vậy: 5/4 x Vận tốc ô tô = 8/4 x vận tốc xe máy

Vậy vận tốc ô tô = 8/5 vận tốc xe máy

Tổng số phần bằng nhau: 5+8=13(phần)

Vận tốc xe ô tô: 65 : 13 x 8 = 40(km/h)

Vận tốc xe máy: 65 - 40 = 25 (km/h)

Đ.số:....

ai trả lời đc câu hỏi ko ạ

Gọi vận tốc xe ô tô là x(km/h) và vận tốc xe máy là y(km/h)

(Điều kiện: x>0; y>0)

Sau 6 giờ xe ô tô đi được 6x(km)

Sau 6h xe máy đi được 6y(km)

Khi hai xe xuất phát cùng lúc thì sau 6 giờ hai xe gặp nhau nên ta có phương trình:

6x+6y=390

=>x+y=65(1)

Độ dài quãng đường xe ô tô đi được trong 3h15p=3,25 giờ là:

\(3,25\cdot x\left(km\right)\)

Độ dài quãng đường còn lại là:

390-3,25x(km)

Trong 4 giờ thì ô tô đi được 4x(km)

Trong 4 giờ thì xe máy đi được 4y(km)

Khi xe ô tô xuất phát trước 3,25h thì hai xe gặp nhau sau 4 giờ nên ta có phương trình:

4x+4y+3,25x=390

=>7,25x+4y=390(2)

từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}x+y=65\\7,25x+4y=390\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4x+4y=260\\7,25x+4y=390\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-3,25x=-130\\x+y=65\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=40\\y=65-40=25\end{matrix}\right.\left(nhận\right)\)

vậy: Vận tốc xe ô tô là 40km/h
Vận tốc xe máy là 25km/h

ĐKXĐ: x<>2 và y>=-1

\(\left\{{}\begin{matrix}\dfrac{1}{x-2}-2\sqrt{y+1}=-4\\\dfrac{2}{x-2}+\sqrt{y+1}=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{2}{x-2}-4\sqrt{y+1}=-8\\\dfrac{2}{x-2}+\sqrt{y+1}=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-5\sqrt{y+1}=-15\\\dfrac{2}{x-2}+\sqrt{y+1}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{y+1}=3\\\dfrac{2}{x-2}=7-3=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y+1=9\\x-2=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=8\\x=\dfrac{5}{2}\end{matrix}\right.\left(nhận\right)\)

ai giải giúp mik ko, tự giải đi nè

\(a=\sqrt[3]{2-\sqrt{3}}+\sqrt[3]{2+\sqrt{3}}\)

=>\(a^3=2-\sqrt{3}+2+\sqrt{3}+3\cdot\left(\sqrt[3]{2-\sqrt{3}}+\sqrt[3]{2+\sqrt{3}}\right)\cdot\sqrt[3]{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)

=>\(a^3=4+3a\)

=>\(a^3-3a=4\)

\(\Leftrightarrow a^2-3=\dfrac{4}{a}\)

\(\left(a^2-3\right)^3\)

\(=\left(\dfrac{4}{a}\right)^3=\dfrac{64}{a^3}\)

\(C=\dfrac{64}{\left(a^2-3\right)^3}-3a\)

\(=64:\dfrac{64}{a^3}-3a\)

=a^3-3a

=4

\(\dfrac{1}{\sqrt[3]{4}+\sqrt[3]{2}+1}=\dfrac{\sqrt[3]{2}-1}{\left(\sqrt[3]{2}-1\right)\left(\sqrt[3]{4}+\sqrt[3]{2}+1\right)}\)

\(=\dfrac{\sqrt[3]{2}-1}{2-1}=\sqrt[3]{2}-1\)