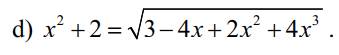\(PT\Leftrightarrow x^4+4x^2+4=4x^3+2x^2-4x+3\)
=>\(x^4-4x^3+2x^2+4x+1=0\)
\(\Leftrightarrow\left(x^2-2x-1\right)^2=0\)
=>x^2-2x-1=0
=>\(x=1\pm\sqrt{2}\)
\(x^2+2=\sqrt{3-4x+2x^2+4x^3}\)
\(\Leftrightarrow\left(x^2+2\right)^2=4x^3+2x^2-4x+3\)
\(\Leftrightarrow\left(x^2\right)^2+2\cdot2\cdot x^2+2^2=4x^3+2x^2-4x+3\)
\(\Leftrightarrow x^4+4x^2+4=4x^3+2x^2-4x+3\)
\(\Leftrightarrow x^4-4x^3+\left(4x^2-2x^2\right)+4x+\left(4-3\right)=0\)
\(\Leftrightarrow x^4-4x^3+2x^2+4x+1=0\)
\(\Leftrightarrow\left(x^2-2x-1\right)^2=0\)
\(\Leftrightarrow x^2-2x-1=0\)
\(\Rightarrow\Delta=\left(-2\right)^2-4\cdot1\cdot-1=8>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{2+2\sqrt{2}}{2}=1+\sqrt{2}\\x_2=\dfrac{2-2\sqrt{2}}{2}=1-\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow x=1\pm\sqrt{2}\)
Để giải phương trình x^2 + 2 = √3 - 4x + 2x^2 + 4x^3, chúng ta cần tìm giá trị của x thỏa mãn phương trình này. Dưới đây là quá trình giải phương trình:
1. Đưa tất cả các thuật ngữ chứa x về cùng một bên của phương trình và để hệ số của x^3 là dương:
4x^3 + 2x^2 + 4x + x^2 + 4x - √3 + 2 = 0
2. Kết hợp các thuật ngữ tương tự:
4x^3 + 3x^2 + 8x - √3 + 2 = 0
3. Giải phương trình này không dễ dàng bằng cách sử dụng phép tính truyền thống. Thay vào đó, chúng ta có thể tìm nghiệm gần đúng bằng phương pháp số học hoặc sử dụng máy tính.
Kết quả gần đúng cho x là khoảng x ≈ 0.287106. Để tìm nghiệm chính xác, bạn có thể sử dụng phần mềm máy tính hoặc phương pháp giải đa thức bậc ba nếu cần.