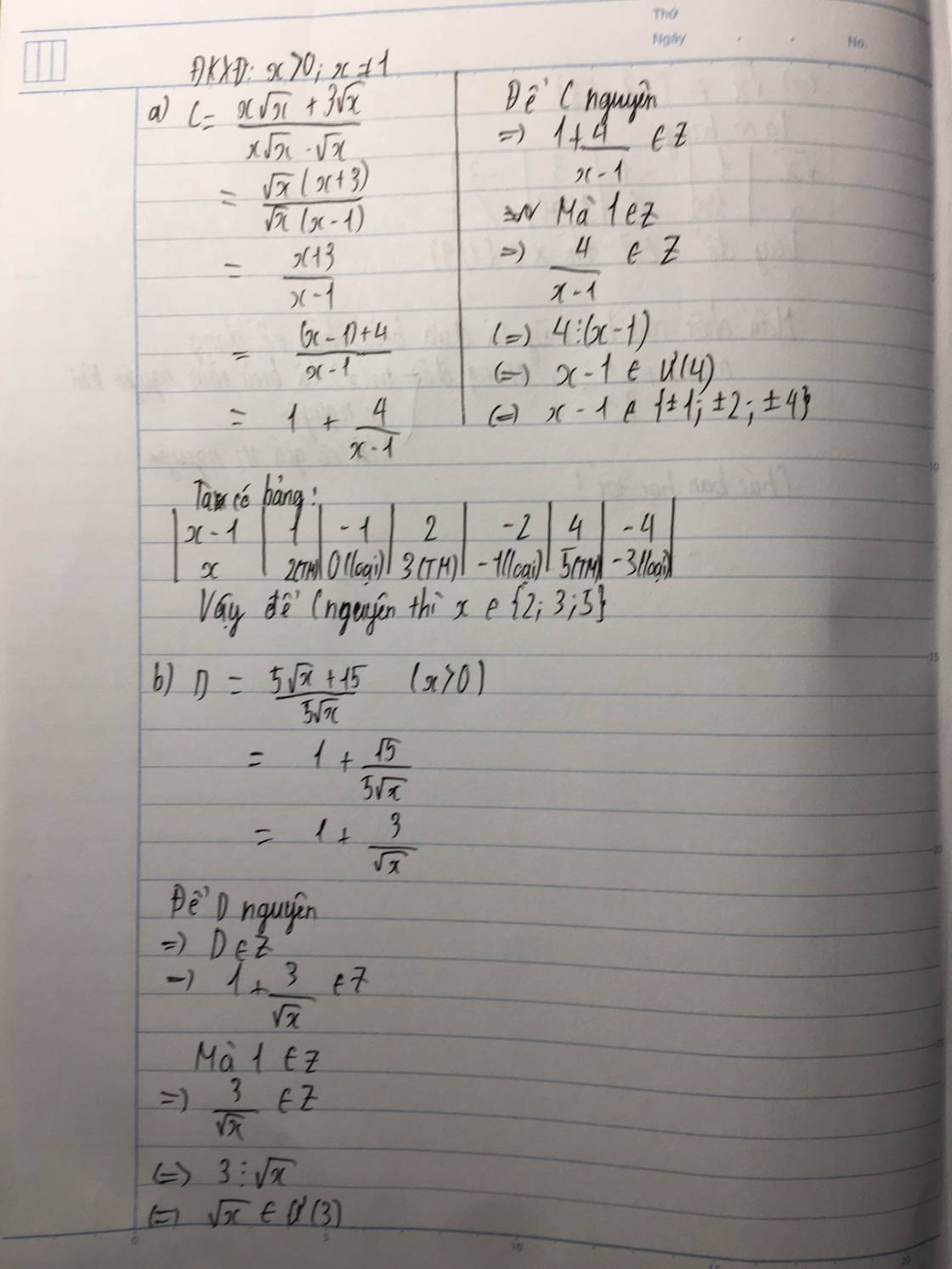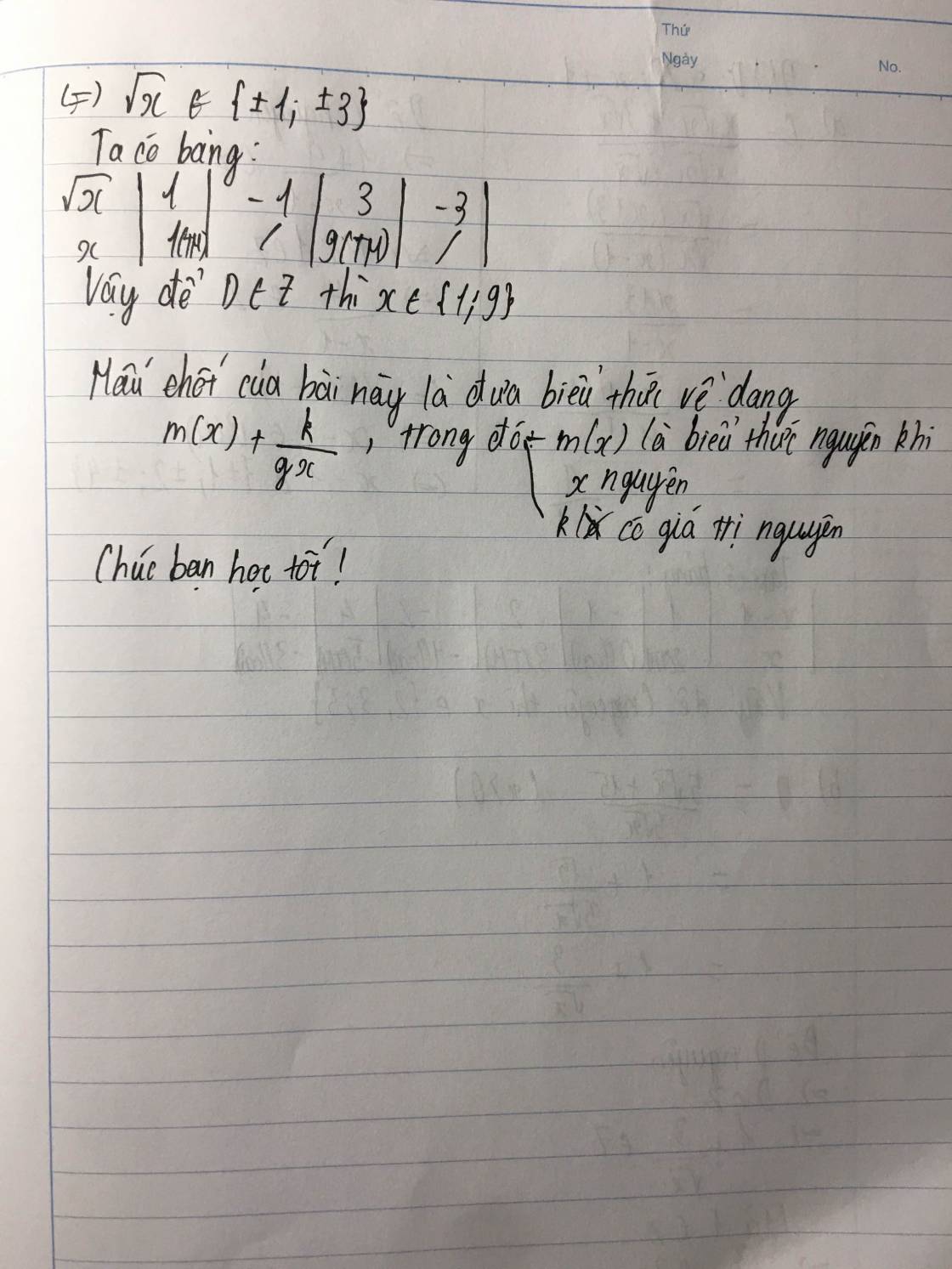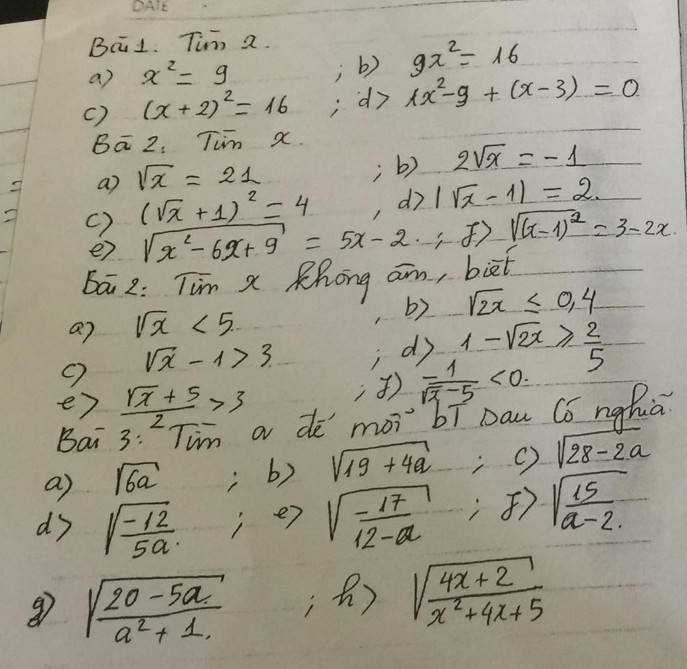
Bài 8: Rút gọn biểu thức chứa căn bậc hai
Bài 1:
a: \(x^2=9\)
=>\(x^2=3^2=\left(-3\right)^2\)
=>\(x=\pm3\)
b: \(9x^2=16\)
=>\(\left[{}\begin{matrix}3x=4\\3x=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
c: \(\left(x+2\right)^2=16\)
=>\(\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)
d: \(x^2-9+\left(x-3\right)=0\)
=>\(\left(x-3\right)\left(x+3\right)+\left(x-3\right)=0\)
=>\(\left(x-3\right)\left(x+3+1\right)=0\)
=>\(\left(x-3\right)\left(x+4\right)=0\)
=>\(\left[{}\begin{matrix}x-3=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\)
Bài 2:
a: ĐKXĐ: x>0
\(\sqrt{x}=21\)
=>\(x=21^2\)
=>\(x=441\)
b: ĐKXĐ: x>=0
\(2\sqrt{x}=-1\)
=>\(\sqrt{x}=-\dfrac{1}{2}\)(vô lý)
Vậy: \(x\in\varnothing\)
c: ĐKXĐ: x>=0
\(\left(\sqrt{x}+1\right)^2=4\)
=>\(\left[{}\begin{matrix}\sqrt{x}+1=2\\\sqrt{x}+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=-3\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}=1\)
=>x=1(nhận)
d: ĐKXĐ: x>=0
\(\left|\sqrt{x}-1\right|=2\)
=>\(\left[{}\begin{matrix}\sqrt{x}-1=2\\\sqrt{x}-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=-1\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}=3\)
=>x=9(nhận)
e: ĐKXĐ: \(x\in R\)
\(\sqrt{x^2-6x+9}=5x-2\)
=>\(\sqrt{\left(x-3\right)^2}=5x-2\)
=>\(\left\{{}\begin{matrix}5x-2>=0\\\left(5x-2\right)^2=\left(x-3\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{5}\\\left(5x-2\right)^2-\left(x-3\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{2}{5}\\\left(5x-2-x+3\right)\left(5x-2+x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{2}{5}\\\left(4x+1\right)\left(6x-5\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{5}\\\left[{}\begin{matrix}x=-\dfrac{1}{4}\left(loại\right)\\x=\dfrac{5}{6}\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy: x=5/6
f: \(\sqrt{\left(x-1\right)^2}=3-2x\)
=>\(\left\{{}\begin{matrix}3-2x>=0\\\left(3-2x\right)^2=\left(x-1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(2x-3\right)^2-\left(x-1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(2x-3-x+1\right)\left(2x-3+x-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(x-2\right)\left(3x-4\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left[{}\begin{matrix}x=2\left(loại\right)\\x=\dfrac{4}{3}\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Rút gọn
C= \( \dfrac{ \dfrac{ x- \sqrt{ x \phantom{\tiny{!}}} }{ \sqrt{ x \phantom{\tiny{!}}} -1 } - \dfrac{ \sqrt{ x \phantom{\tiny{!}}} +1 }{ x+ \sqrt{ x \phantom{\tiny{!}}} } }{ \dfrac{ \sqrt{ x \phantom{\tiny{!}}} +1 }{ x } } \)
Lời giải:
Xét tử thức:
\(\frac{x-\sqrt{x}}{\sqrt{x}-1}-\frac{\sqrt{x}+1}{x+\sqrt{x}}=\frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}-1}-\frac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}+1)}=\sqrt{x}-\frac{1}{\sqrt{x}}=\frac{x-1}{\sqrt{x}}\)
\(\Rightarrow C=\frac{x-1}{\sqrt{x}}: \frac{\sqrt{x}+1}{x}=\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{\sqrt{x}}.\frac{x}{\sqrt{x}+1}=\sqrt{x}(\sqrt{x}-1)\)
Đúng 3
Bình luận (0)
P=x+3/căn x +3 tìm giá trị nhỏ nhất của p
\(P=\dfrac{x+3}{\sqrt{x}+3}\) (ĐK: \(x\ge0\))
Mà: \(x\ge0\Rightarrow\left\{{}\begin{matrix}x+3\ge3\\\sqrt{x}+3\ge3\end{matrix}\right.\) nên:
\(P=\dfrac{x+3}{\sqrt{x}+3}\ge\dfrac{3}{3}=1\)
Dấu "=" xảy ra:
\(\dfrac{x+3}{\sqrt{x}+3}=1\)
\(\Leftrightarrow x=\sqrt{x}\)
\(\Leftrightarrow x=0\left(tm\right)\)
Vậy: \(P_{min}=1\) khi \(x=0\)
Đúng 0
Bình luận (0)
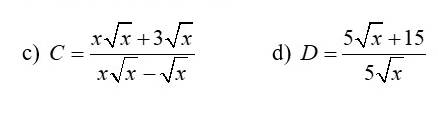
Tìm x nguyên để các biểu thức sau đạt giá trị nguyên
Bai 1 Cho P = (sqrt(x))/(sqrt(x + 2)) (sqrt(x - 1))/(5x - 2) - (2 + 55x)/(x - 4) a. Rút b. tinx * de*p_{1}
Nhờ mn giúp mik vs ạ.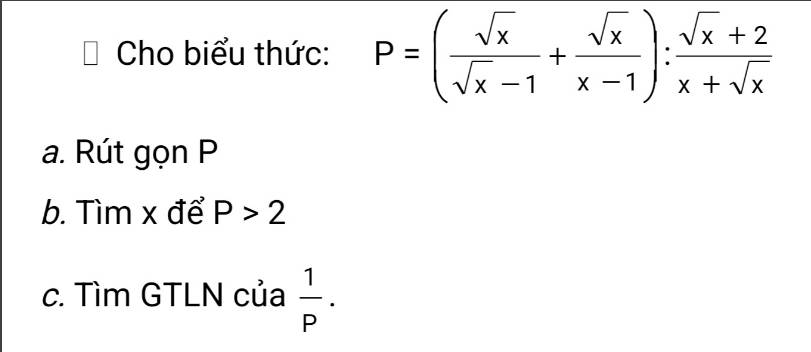
Lời giải:
a. ĐKXĐ: $x>0; x\neq 1$
\(P=\left[\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}+\frac{\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}\right].\frac{x+\sqrt{x}}{\sqrt{x}+2}\)
\(=\frac{x+\sqrt{x}+\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{x}{\sqrt{x}-1}\)
b.
$P>2 \Leftrightarrow \frac{x}{\sqrt{x}-1}-2>0$
$\Leftrightarrow \frac{x-2\sqrt{x}+2}{\sqrt{x}-1}>0$
$\Leftrightarrow \frac{(\sqrt{x}-1)^2+1}{\sqrt{x}-1}>0$
$\Leftrightarrow \sqrt{x}-1>0$ (do $(\sqrt{x}-1)^2+1>0$)
$\Leftrightarrow x>1$
Kết hợp đkxđ suy ra $x>1$
c.
$\frac{1}{P}=\frac{\sqrt{x}-1}{x}$
Áp dụng BĐT Cô-si:
$x+4\geq 4\sqrt{x}\Rightarrow x\geq 4(\sqrt{x}-1)$
$\Rightarrow \frac{\sqrt{x}-1}{x}\leq \frac{\sqrt{x}-1}{4(\sqrt{x}-1)}=\frac{1}{4}$
Vậy $\frac{1}{P}$ max $=\frac{1}{4}$ khi $x=4$
Đúng 2
Bình luận (1)
2) Cho tam giác ABC vuông tại A, đường cao AH. a) Giả sử AB = 6cm AC = 8cm hãy tính độ dài đoạn thẳng BC, AH,ACB (số đo góc làm tròn đến phút). b) Gọi điểm E và F lần lượt là hình chiếu của điểm H trên cạnh AB,AC . Chứng minh rằng AE .AB=AF.AC, từ đó suy ra AFE = ABC c) Đường trung tuyến AI của tam giác ABC cắt cạnh EF tại K. Chứng minh rằng: 3 = (KF)/(BC) cos^3 B .sin B= x- n-
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=4,8cm
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{ACB}\simeq36^052'\)
b: ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF đồng dạng với ΔACB
=>\(\widehat{AFE}=\widehat{ABC}\)
Đúng 1
Bình luận (0)
(2,0 điểm) Cho các biểu thức A = (sqrt(x))/(2sqrt(x) - 4); B = (sqrt(x))/(sqrt(x) + 2) +3(sqrt(x)-x /x-4 với x >= 0 ,x ne4 1) Tính giá trị của A khi x = 36 . 2) Rút gon biểu thức C = B : A . 3) Tìm các giá trị của x để C. sqrt(x) < 4/3 .
1: Khi x=36 thì \(A=\dfrac{6}{2\cdot6-4}=\dfrac{6}{12-4}=\dfrac{6}{8}=\dfrac{3}{4}\)
2:
ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x< >4\end{matrix}\right.\)
\(C=B:A\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}-x}{x-4}\right):\dfrac{\sqrt{x}}{2\sqrt{x}-4}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)+3\sqrt{x}-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{2\left(\sqrt{x}-2\right)}{\sqrt{x}}\)
\(=\dfrac{x-2\sqrt{x}+3\sqrt{x}-x}{\sqrt{x}+2}\cdot\dfrac{2}{\sqrt{x}}=\dfrac{2}{\sqrt{x}+2}\)
3: \(C\cdot\sqrt{x}< \dfrac{4}{3}\)
=>\(\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{4}{3}< 0\)
=>\(\dfrac{2\sqrt{x}\cdot3-4\left(\sqrt{x}+2\right)}{3\left(\sqrt{x}+2\right)}< 0\)
=>\(6\sqrt{x}-4\sqrt{x}-8< 0\)
=>\(2\sqrt{x}-8< 0\)
=>\(\sqrt{x}< 4\)
=>\(0< =x< 16\)
Kết hợp ĐKXĐ của C, ta được: \(\left\{{}\begin{matrix}0< x< 16\\x< >4\end{matrix}\right.\)
Đúng 1
Bình luận (0)
√2-√3 . (√6+√2) Cảm ơn bồ ❤
\(=\sqrt{4-2\sqrt{3}}\left(\sqrt{3}+1\right)=\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)=2\)
Đúng 1
Bình luận (0)
sqrt(4x - 20) + 3sqrt((x - 5)/9) = 3
Điều kiện: \(x\ge5\).
Phương trình tương đương với:
\(\sqrt{4\left(x-5\right)}+\dfrac{3\sqrt{x-5}}{\sqrt{9}}=3\)
\(\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}=3\)
\(\Leftrightarrow\sqrt{x-5}=1\Rightarrow x-5=1\Leftrightarrow x=6\left(TM\right)\)
Vậy: Phương trình có tập nghiệm \(S=\left\{6\right\}\).
Đúng 1
Bình luận (0)