3.(-2)5x+8+52=1
giúp mình với ạ
3.(-2)5x+8+52=1
giúp mình với ạ
\(3\cdot(-2)^{5x+8}+5^2=1\\\Rightarrow 3\cdot(-2)^{5x+8}+25=1\\\Rightarrow 3\cdot(-2)^{5x+8}=1-25\\\Rightarrow 3\cdot(-2)^{5x+8}=-24\\\Rightarrow (-2)^{5x+8}=-24:3\\\Rightarrow (-2)^{5x+8}=-8\\\Rightarrow (-2)^{5x+8}=(-2)^3\\\Rightarrow 5x+8=3\\\Rightarrow 5x=3-8\\\Rightarrow 5x=-5\\\Rightarrow x=-5:5\\\Rightarrow x=-1\)
-2/3 mũ 3 : 0,(3) +(2/3) mũ 2
\(-\dfrac{2}{3^3}:0,\left(3\right)+\left(\dfrac{2}{3}\right)^2\)
\(=\dfrac{-2}{27}:\dfrac{1}{3}+\dfrac{4}{9}\)
\(=\dfrac{-2}{9}+\dfrac{4}{9}=\dfrac{2}{9}\)
`#3107.101107`
`(-2/3)^3 \div 0,(3) + (2/3)^2`
`= (-2/3)^3 \div 1/3 + (2/3)^2`
`= (-2/3)^3 * 3 + (2/3)^2`
`= (2/3)^2 * (-2/3 * 3 + 1)`
`= 4/9 * (-2+1)`
`= 4/9 * (-1)`
`= -4/9`
CĂN 16/9 + 2/3 mũ 9 : -2/3 mũ 8 - giá trị tuyệt đối của -2023
\(\sqrt{\dfrac{16}{9}}+\left(\dfrac{2}{3}\right)^9:\left(-\dfrac{2}{3}\right)^8-\left|-2023\right|\)
\(=\dfrac{4}{3}-2023+\left(\dfrac{2}{3}\right)^9:\left(\dfrac{2}{3}\right)^8\)
\(=\dfrac{4}{3}+\dfrac{2}{3}-2023\)
=2-2023
=-2021
2x+11 . 34 = 12x
\(2^x+11.3^4=12^x\)
\(2^x\)chẵn, \(11.3^4\) lẻ => \(2^x+11.3^4\) lẻ(1)
Mà \(12^x\) chẵn(2)
Từ (1) và (2) => \(VT\ne VP\)
=> không tồn tại x thỏa mã phương trình
Cách trên là với điều kiện \(x\in N\cdot\) nha, cách này là với trường hợp không có điều kiện của x
\(2^x+11.3^4=12^x=2^{2x}.3^x\)
\(2^x\left(6^x-1\right)=11.3^4\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2^x=11\\6^x-1=3^4\end{matrix}\right.\\\left\{{}\begin{matrix}6^x=12\\2^x=3^4\end{matrix}\right.\end{matrix}\right.\)
+) Nếu x=0 => Loại
+) Nếu \(x\in N^{\cdot}\)
-) \(2^x=11\) (Loại vì 2x chãn)
-) \(6^x=12\Leftrightarrow2^x.3^x=2^2.3\)
\(\Leftrightarrow\left\{{}\begin{matrix}2^x=2^2\\3^x=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=1\end{matrix}\right.\) (Loại)
+) Nếu x>0; \(x\notin Z\)
=> \(2^x;6^x\notin Z\) (Loại)
+) Nếu x<0 => \(\left\{{}\begin{matrix}2^x< 2\\6^x< 6\end{matrix}\right.\) (Loại)
=> Không tồn tại x thỏa mãn phương trình
M=21.x^2.y+4.x.y^2 với x,y thỏa mãn (x-2)^4+(2y-1)^2024 ≤ 0
\(\left(x-2\right)^4+\left(2y-1\right)^{2024}\le0\left(1\right)\)
Vì \(\left\{{}\begin{matrix}\left(x-2\right)^4\ge0\forall x\\\left(2y-1\right)^{2024}\ge0\forall x\end{matrix}\right.\)
\(\Rightarrow\left(x-2\right)^4+\left(2y-1\right)^{2024}\ge0\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\left(x-2\right)^4+\left(2y-1\right)^{2024}=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
\(M=21.2^2.\dfrac{1}{2}+4.2.\left(\dfrac{1}{2}\right)^2=21.2+4.2.\dfrac{1}{4}=42+2=44\)
Ta có: \(\left(x-2\right)^4\ge0\forall x\)
\(\left(2y-1\right)^{2024}\ge0\forall y\)
\(\Rightarrow\left(x-2\right)^4+\left(2y-1\right)^{2024}\ge0\forall x;y\)
Mặt khác: \(\left(x-2\right)^4+\left(2y-1\right)^{2024}\le0\)
nên \(\left(x-2\right)^4+\left(2y-1\right)^{2024}=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^4=0\\\left(2y-1\right)^{2024}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\2y-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
Thay \(x=2\) và \(y=\dfrac{1}{2}\) vào \(M\), ta được:
\(M=21\cdot2^2\cdot\dfrac{1}{2}+4\cdot2\cdot\left(\dfrac{1}{2}\right)^2\)
\(=42+2\)
\(=44\)
Vậy \(M=44\) tại \(x=2;y=\dfrac{1}{2}\).
#\(Toru\)
1/3+1/3 mũ 2+...+1/3 mũ 100
Đặt `A=1/3+1/(3^2)+...+1/(3^100)`
`3A=1+1/3+...+1/(3^99)`
`3A-A=(1+1/3+...+1/(3^99))-(1/3+1/(3^2)+...+1/(3^100))`
`2A=1-1/(3^100)`
`A=(1-1/(3^100))/2`
Đặt \(A=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{100}}\)
\(3\cdot A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)
\(3A-A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{100}}\right)\)
\(2A=1-\dfrac{1}{3^{100}}\)
\(\Rightarrow A=\dfrac{3^{100}-1}{3^{100}}:2=\dfrac{3^{100}-1}{2\cdot3^{100}}\)
#\(Toru\)
(3x-5y)^2 + (xy-135)^2=0
\(\left(3x-5y\right)^2+\left(xy-135\right)^2=0\)
Vì \(\left\{{}\begin{matrix}\left(3x-5y\right)^2\ge0\forall x,y\\\left(xy-135\right)^2\ge0\forall x,y\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3x-5y=0\\xy-135=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}y\\xy=135\end{matrix}\right.\)
\(\Rightarrow\dfrac{5}{3}y.y=135\)\(\Rightarrow y^2=81\)
\(\Leftrightarrow\left[{}\begin{matrix}y=9\Rightarrow x=15\\y=-9\Rightarrow x=-15\end{matrix}\right.\)
Ta có: \(\left(3x-5y\right)^2\ge0\forall x;y\)
\(\left(xy-135\right)^2\ge0\forall x;y\)
\(\Rightarrow\left(3x-5y\right)^2+\left(xy-135\right)^2\ge0\forall x\)
Mặt khác: \(\left(3x-5y\right)^2+\left(xy-135\right) ^2=0\)
nên: \(\left\{{}\begin{matrix}\left(3x-5y\right)^2=0\\\left(xy-135\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-5y=0\\xy-135=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=5y\\xy=135\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}y\\\dfrac{5}{3}y^2=135\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}y\\y^2=81\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}y\\\left[{}\begin{matrix}y=9\\y=-9\end{matrix}\right.\end{matrix}\right.\)
\(+,TH1:y=9\Leftrightarrow x=\dfrac{5}{3}\cdot9=15\left(tm\right)\)
\(+,TH2:y=-9\Leftrightarrow x=\dfrac{5}{3}\cdot\left(-9\right)=-15\left(tm\right)\)
Vậy ...
#\(Toru\)
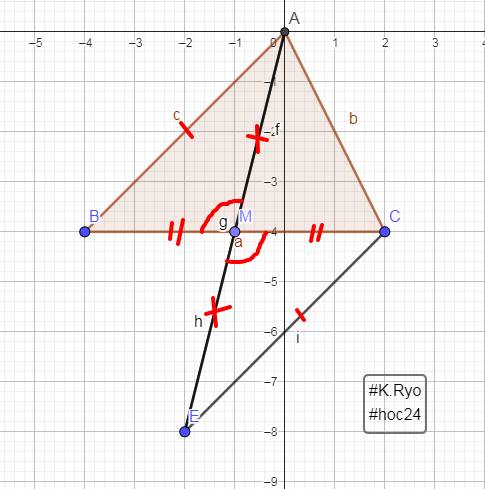
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
a. CMR: Tam giác ABM = tam giác ECM
b. CMR: AB = CE
`# \text {DNamNguyenV}`
`a,`
Ta có: M là trung điểm của BC
`=> \text {MB = MC}`
Xét `\Delta ABM` và `\Delta ECM`:
`\text {MA = ME (gt)}`
\(\text{ }\widehat{\text{ AMB}}=\widehat{\text{EMC}}\left(\text{2 góc đối đỉnh}\right)\)
`\text {MB = MC}`
`=> \Delta ABM = \Delta ECM (c - g - c)`
`b,`
Vì `\Delta ABM = \Delta ECM (a)`
`=> \text {AB = CE (2 góc tương ứng)}`
Cho tam giác ABC. Có góc A = 90 độ. Trên cạnh BC lấy điểm E sao cho BA = BE. Tia pg của góc B cắt AC tại D.
a. CMR: Tam giác ABD = tam giác EBD
b. CMR: DA = DE
?(có vẽ hình)
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
`#040911`
`A = 1 + 2 + 4 + 8 + ... + 8192`
`A = 1 + 2 + 2^2 + 2^3 + ... + 2^13`
`2A = 2 + 2^2 + 2^3 + 2^4 + ... + 2^14`
`2A - A = (2 + 2^2 + 2^3 + ... + 2^14) - (1 + 2 + 2^2 + ... + 2^13)`
`A = 2 + 2^2 + 2^3 + ... + 2^14 - 1 - 2 - 2^2 - ... - 2^13`
`A = 2^14 - 1`
Vậy, `A = 2^14 - 1.`
A=1+2+2^2+...+2^13
=>2A=2+2^2+2^3+...+2^14
=>2A-A=2^14-1
=>A=2^14-1