Cho tam giác ABC đều nội tiếp (O) lấy M thuộc BC
Chứng minh rằng: MB+MC=MA
Bài 3: Góc nội tiếp
Trên cạnh MA, lấy H sao cho MH=MB
Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB
\(\widehat{AMB}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{AMB}=\widehat{ACB}=60^0\)
Xét ΔMHB có MB=MH và \(\widehat{HMB}=60^0\)
nên ΔMHB đều
=>\(\widehat{MHB}=60^0=\widehat{MBH}\) và MB=MH=BH
Ta có: \(\widehat{AHB}+\widehat{BHM}=180^0\)(hai góc kề bù)
=>\(\widehat{AHB}+60^0=180^0\)
=>\(\widehat{AHB}=120^0\)
Xét (O) có A,B,M,C cùng thuộc (O)
nên ABMC là tứ giác nội tiếp
=>\(\widehat{BAC}+\widehat{BMC}=180^0\)
=>\(\widehat{BMC}=180^0-60^0=120^0\)
=>\(\widehat{AHB}=\widehat{BMC}\)
Xét (O) có
\(\widehat{BAM}\) là góc nội tiếp chắn cung BM
\(\widehat{BCM}\) là góc nội tiếp chắn cung BM
Do đó: \(\widehat{BAM}=\widehat{BCM}\)
Ta có: \(\widehat{AHB}+\widehat{HAB}+\widehat{HBA}=180^0\)
\(\widehat{BMC}+\widehat{MBC}+\widehat{MCB}=180^0\)
mà \(\widehat{AHB}=\widehat{BMC}=120^0;\widehat{HAB}=\widehat{MCB}\)
nên \(\widehat{HBA}=\widehat{MBC}\)
Xét ΔHBA và ΔMBC có
HB=MB
\(\widehat{HBA}=\widehat{MBC}\)
BA=BC
Do đó: ΔHBA=ΔMBC
=>HA=MC
Ta có: AH+HM=AM
mà AH=MC và HM=MB
nên MB+MC=MA
Đúng 1
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB kẻ tiếp tuyến Bx với nửa đường tròn, gọi C là điểm trên nửa đường tròn sao cho cung CB bằng cung CA. D là một điểm tùy ý trên cung CD (D khác C và B) Các tia AC, AD cắt tia Bx theo thứ tự E và F a) tính sd cung CA,CB, so Sánh góc DAB và DOB b) cm bx là tiếp tuyến của đg tròn (O)
a.
Do \(\stackrel\frown{CB}=\stackrel\frown{CA}\Rightarrow sđ\stackrel\frown{CB}=sđ\stackrel\frown{CA}=\dfrac{1}{2}sđ\stackrel\frown{AB}=\dfrac{1}{2}.180^0=90^0\)
\(\widehat{DAB}\) và \(\widehat{DOB}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BD
\(\Rightarrow\widehat{DAB}=\dfrac{1}{2}\widehat{DOB}\)
b.
Chắc em ghi sai đề, giả thiết ban đầu đã cho sẵn Bx là tiếp tuyến của (O) rồi sao còn yêu cầu chứng minh nữa?
Đúng 0
Bình luận (1)
H24
17 tháng 2 2024 lúc 17:01
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R). 3 đường cao AD, BE, CF cắt nhau tại H. Kẻ đường kính AK. Kéo dài AD cắt (O;R) tại M. Gọi I là trung điểm của BC
a) Cminh 3 điểm H I K thẳng hàng
b) Cminh tứ giác BMKC là hình thang cân
c) Nối OH cắt AI tại G. Cminh G là trọng tâm của tam giác ABC
a: Xét (O) có
ΔABK nội tiếp
AK là đường kính
Do đó: ΔABK vuông tại B
=>BK\(\perp\)AB
mà CH\(\perp\)AB
nên CH//BK
Xét (O) có
ΔACK nội tiếp
AK là đường kính
Do đó: ΔACK vuông tại C
=>AC\(\perp\)CK
mà AC\(\perp\)BH
nên BH//CK
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà I là trung điểm của BC
nên I là trung điểm của HK
=>H,I,K thẳng hàng
b: Xét (O) có
ΔAMK nội tiếp
AK là đường kính
Do đó: ΔAMK vuông tại M
=>AM\(\perp\)MK
mà AM\(\perp\)BC
nên MK//BC
=> BMKC là hình thang
Ta có: B,M,K,C cùng thuộc (O)
=>BMKC là tứ giác nội tiếp
=>\(\widehat{MBC}+\widehat{MKC}=180^0\)
mà \(\widehat{MBC}+\widehat{BMK}=180^0\)(hai góc trong cùng phía, MK//BC)
nên \(\widehat{BMK}=\widehat{MKC}\)
Xét hình thang BMKC có \(\widehat{BMK}=\widehat{MKC}\)
nên BMKC là hình thang cân
Đúng 2
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn nội tiếp (O) các đường cao BH,CK cắt nhai tại I cà cắt (O) tại D và E
Chứng minh rằng: cung AE = cung AD
Ta có: \(\widehat{ABH}+\widehat{BAC}=90^0\)(ΔAHB vuông tại H)
\(\widehat{ACK}+\widehat{BAC}=90^0\)(ΔAKC vuông tại K)
Do đó: \(\widehat{ABH}=\widehat{ACK}\)
=>\(\widehat{ABD}=\widehat{ACE}\)
Xét (O) có
\(\widehat{ABD}\) là góc nội tiếp chắn cung AD
\(\widehat{ACE}\) là góc nội tiếp chắn cung AE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: \(sđ\stackrel\frown{AD}=sd\stackrel\frown{AE}\)
Đúng 1
Bình luận (0)
va AD. Citing minh MN // AC. Bài 6: (2,5 điểm) Cho tam giác ABC vuông tại A, đường tròn tâm O đường kinh AB cắt BC tại D. a) Chứng minh AC^ angle = CD .Cl b) Gọi I là trung điểm của BD, tiếp tuyến tại D của đường minh rằng FB là tiếp tuyến của (O). tròn (O) cắt AC tại E và cắt tia OI tại F. Chứng c) Giả sử AB = 6 cm, AC = 8 cm. Tính diện tích của tứ giác ABFE.
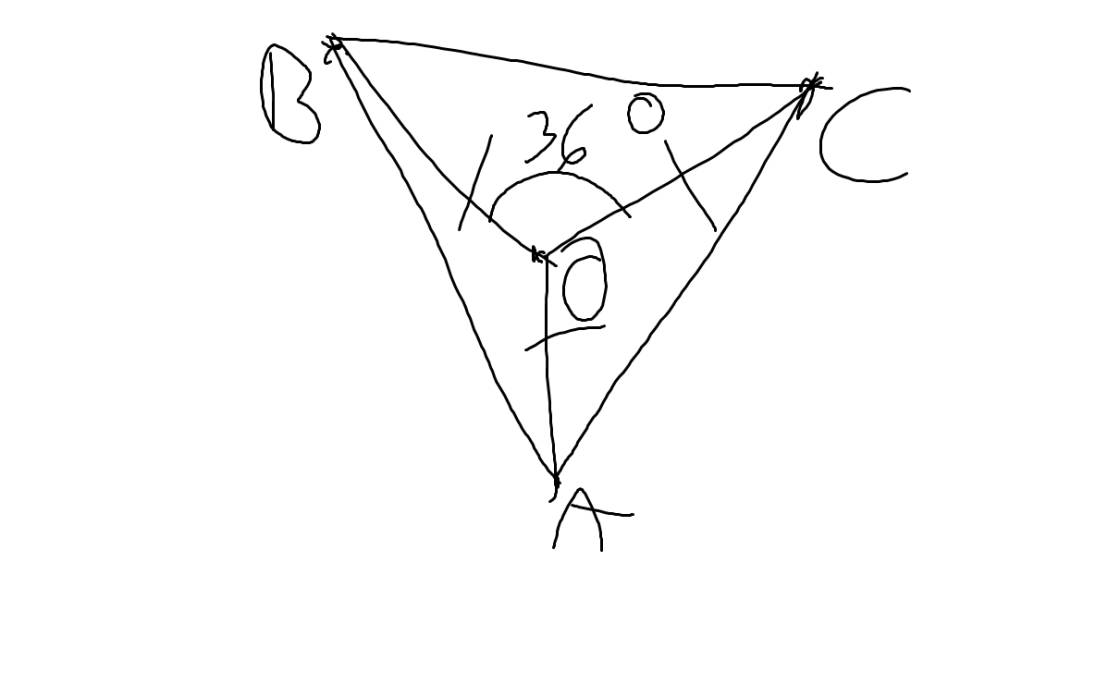
Trên một sân bóng, khi trái bóng được dặt tại điểm phạt đền thì có góc sút bằng 36 độ và trái bóng cách mỗi cọc gôn 11,6m. Hỏi khi trái bóng đặt ở vị trí cách điểm phạt đền 11,6m thì góc sút bằng bao nhiêu
Gọi B,C lần lượt là các cọc gôn,A là điểm cách chấm phạt đền 11,6m, O là chấm phạt đền
Theo đề, ta có: OA=OB=OC=11,6(m) và \(\widehat{BOC}=36^0\)
=>O là tâm đường tròn ngoại tiếp ΔABC
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
=>\(\widehat{BAC}=\dfrac{1}{2}\cdot\widehat{BOC}\)
=>\(\widehat{BAC}=\dfrac{1}{2}\cdot36^0=18^0\)
Đúng 0
Bình luận (0)
H24
15 tháng 10 2023 lúc 7:55
Cho tam giác ABC nội tiếp đường tròn (O), có B, C, O cố định. Hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF. Gọi M là trung điểm của BCa) Chứng minh: AB.AE AD.ACb) Tứ giác BFCH là hình gì?c) Chứng minh ba điểm H, M, F thẳng hàng và OM dfrac{1}{2}AH1
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O), có B, C, O cố định. Hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF. Gọi M là trung điểm của BCa) Chứng minh: AB.AE = AD.ACb) Tứ giác BFCH là hình gì?c) Chứng minh ba điểm H, M, F thẳng hàng và OM = \(\dfrac{1}{2}\)AH
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB đồng dạng với ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)
b: Xét (O) có
ΔABF nội tiếp
AF là đường kính
Do đó: ΔABF vuông tại B
=>BF vuông góc AB
mà CH vuông góc AB
nên BF//CH
Xét (O) có
ΔACF nội tiếp
AF là đường kính
Do đó: ΔACF vuông tại C
=>AC vuông góc CF
mà AC vuông góc BH
nên BH//CF
Xét tứ giác BHCF có
BH//CF
BF//CH
Do đó: BHCF là hình bình hành
c: BHCF là hình bình hành
=>BC cắt HF tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HF
=>H,M,F thẳng hàng
Đúng 1
Bình luận (0)
Cho đường tròn tâm O đường kính AB, trên cùng một nửa đường tròn (O) lấy hai điểm G và E ( theo thứ tự A,G,E,D) sao cho tia EG cắt tia BA tại D. Đg thẳng vuông góc với BD tại D cắt BE tại C, đg thẳng CA cắt đg tròn (O) tại điểm thứ hai là F. Chứng minh tứ giác EADC nội tiếp
Giúp mjk vs mjk đg cần gấp ạ
Em tự vẽ hình nhé!
Có: \(\widehat{CDA}=90^o\)
\(\widehat{CEA}=\widehat{BEA}=90^o\)
\(\Rightarrow\widehat{CDA}+\widehat{CEA}=90^o+90^o=180^o\)
Do đó: tứ giác EADC nội tiếp.
Đúng 1
Bình luận (0)
Cho đường tròn (o) đk AB,trên cung AB lấy M sao cho số đo AM=120°.tiếp tuyến A và M cắt nhau ở c a) tính ABM b) cmr AOMC nội tiếp c) cmr BM//OC Vẽ hình giúp em với ạ
a: góc ABM=1/2*120=60 độ
b: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
c: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM
mà OA=OM
nên OC là trung trực của AM
=>OC vuông góc AM
góc AMB=1/2*180=90 độ
=>MB vuông góc AM
=>MB//OC
Đúng 0
Bình luận (0)
Cho ∆nhọn ABC nội tiếp đường tròn(O) gọi M là giao điểm bất kì trên cung nhỏ BC của đường tròn (O) CM không trùng với BC kẻ MH vuông góc với đường thẳng AB tại H MK vuông góc với đường thẳng AC tại K a.chứng minh tứ giác AHMK nội tiếp b.chứng minh MH.MC=MK.MB
a: góc AHM+góc AKM=90+90=180 độ
=>AHMK là tứ giác nội tiếp
b: Xét ΔMBH vuông tại H và ΔMCK vuông tại K có
góc MBH=góc MCK
=>ΔMBH đồng dạng với ΔMCK
=>MB/MC=MH/MK
=>MB*MK=MC*MH
Đúng 0
Bình luận (0)