Bài 5: Góc có đỉnh bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn.
Nội dung lý thuyết
Các phiên bản khác1. Góc có đỉnh bên trong đường tròn
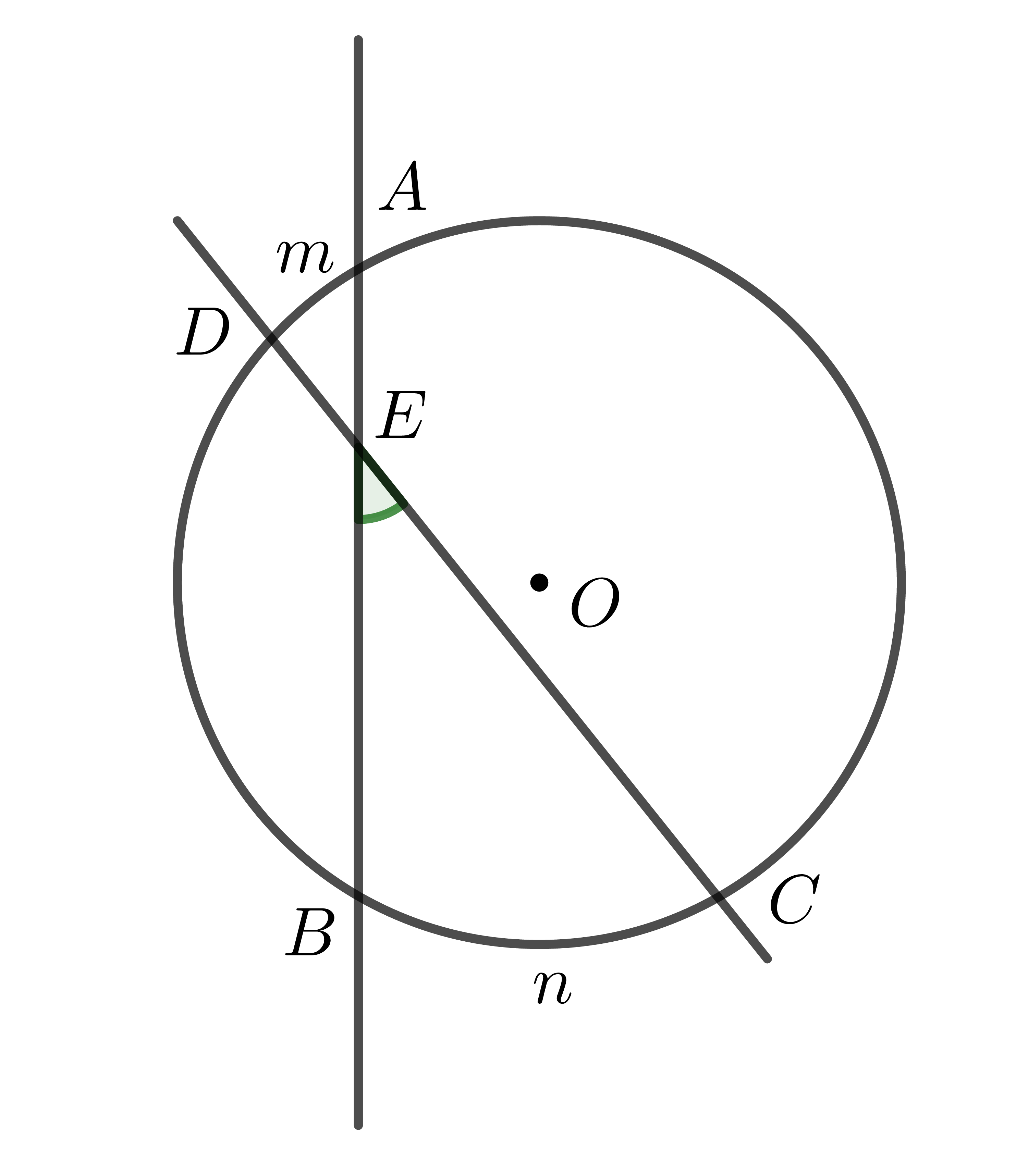
+) Góc \(\widehat{BEC}\) có đỉnh \(E\) nằm trong đường tròn \(\left(O\right)\) được gọi là góc có đỉnh ở bên trong đường tròn.
+) Mỗi góc có đỉnh nằm trong đường tròn chắn hai cung: một cung nằm trong góc, một cung nằm trong góc đối đỉnh của góc đó.
Ví dụ: Trong hình trên, góc \(\widehat{BEC}\) chắn hai cung \(\stackrel\frown{BnC}\) và \(\stackrel\frown{AmD}\).
+) Định lí:
Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Ta có thể chứng minh định lí này như sau:
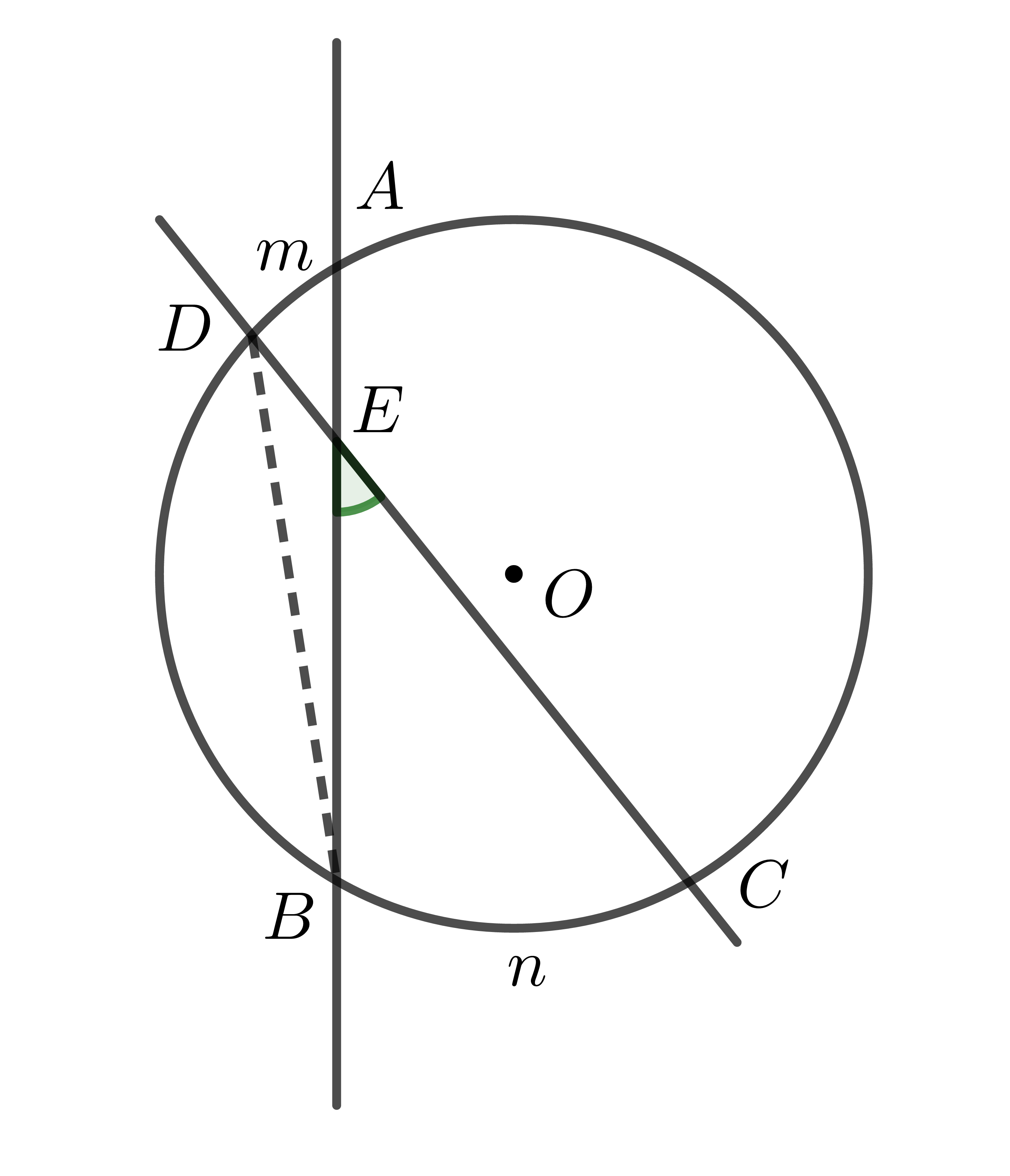
Ta có: \(\widehat{BEC}\) là góc ngoài của tam giác \(BDE\) \(\Rightarrow\widehat{BEC}=\widehat{BDC}+\widehat{DBA}\)
Mặt khác, theo tính chất của góc nội tiếp, ta có: \(\left\{{}\begin{matrix}\widehat{BDC}=\dfrac{1}{2}sđ\stackrel\frown{BnC}\\\widehat{DBA}=\dfrac{1}{2}sđ\stackrel\frown{AmD}\end{matrix}\right.\)
\(\Rightarrow\widehat{BEC}=\dfrac{sđ\stackrel\frown{BnC}+sđ\stackrel\frown{AmD}}{2}\) (định lí được chứng minh).
@59556@@59538@
2. Góc có đỉnh nằm ngoài đường tròn
+) Góc có đỉnh nằm ngoài đường tròn:
- Có đỉnh là một điểm nằm ngoài đường tròn.
- Các cạnh đều có điểm chung với đường tròn.
+) Các góc trong hình vẽ dưới đây là góc có đỉnh nằm ngoài đường tròn:
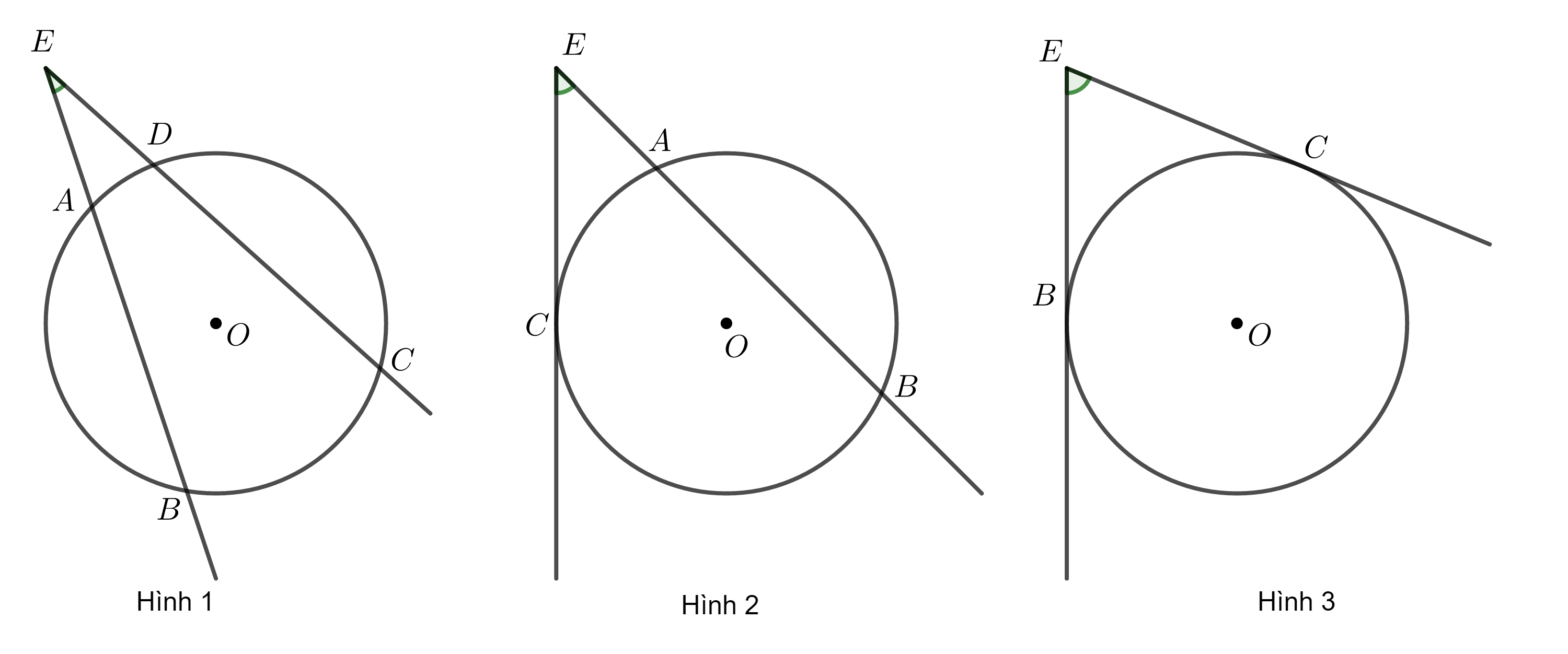
Hình 1: Góc \(\widehat{BEC}\) chắn hai cung nhỏ \(AD,BC\).
Hình 2: Góc \(\widehat{BEC}\) chắn hai cung nhỏ \(AC,BC\).
Hình 3: Góc \(\widehat{BEC}\) chắn cung nhỏ \(BC\) và cung lớn \(BC\).
+) Định lí:
Số đo của góc có đỉnh nằm ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Ta có thể chứng minh định lí trên bằng cách chia 3 trường hợp:
a) Trường hợp 1:
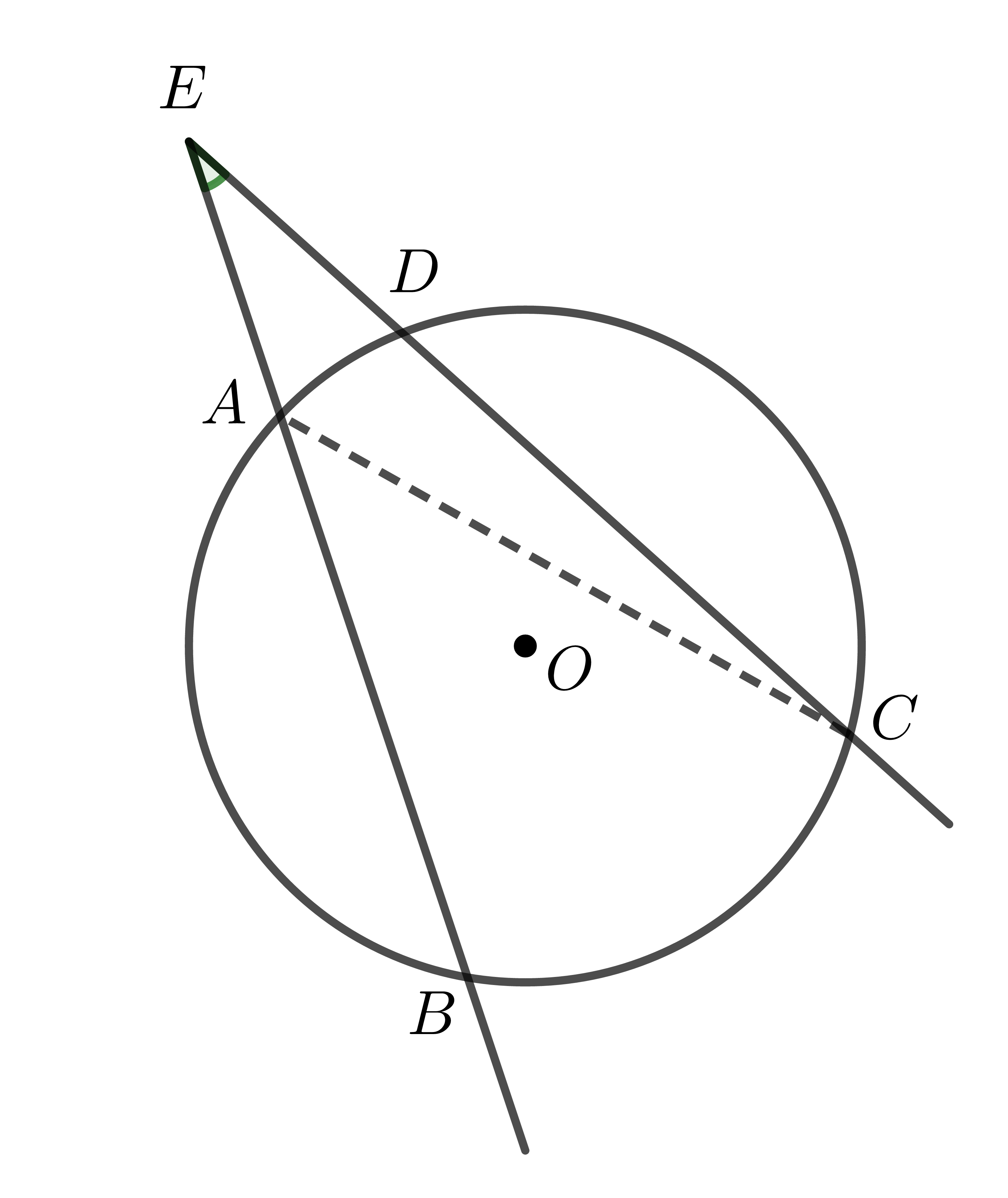
Do \(\widehat{BAC}\) là góc ngoài của tam giác \(EAC\)
\(\Rightarrow\widehat{BAC}=\widehat{BEC}+\widehat{ECA}\)
\(\Rightarrow\widehat{BEC}=\widehat{BAC}-\widehat{ECA}=\dfrac{1}{2}sđ\widehat{BC}-\dfrac{1}{2}sđ\stackrel\frown{AD}\) (tính chất góc nội tiếp)
\(\Rightarrow\widehat{BEC}=\dfrac{sđ\stackrel\frown{BC}-sđ\stackrel\frown{AD}}{2}\).
b) Trường hợp 2:
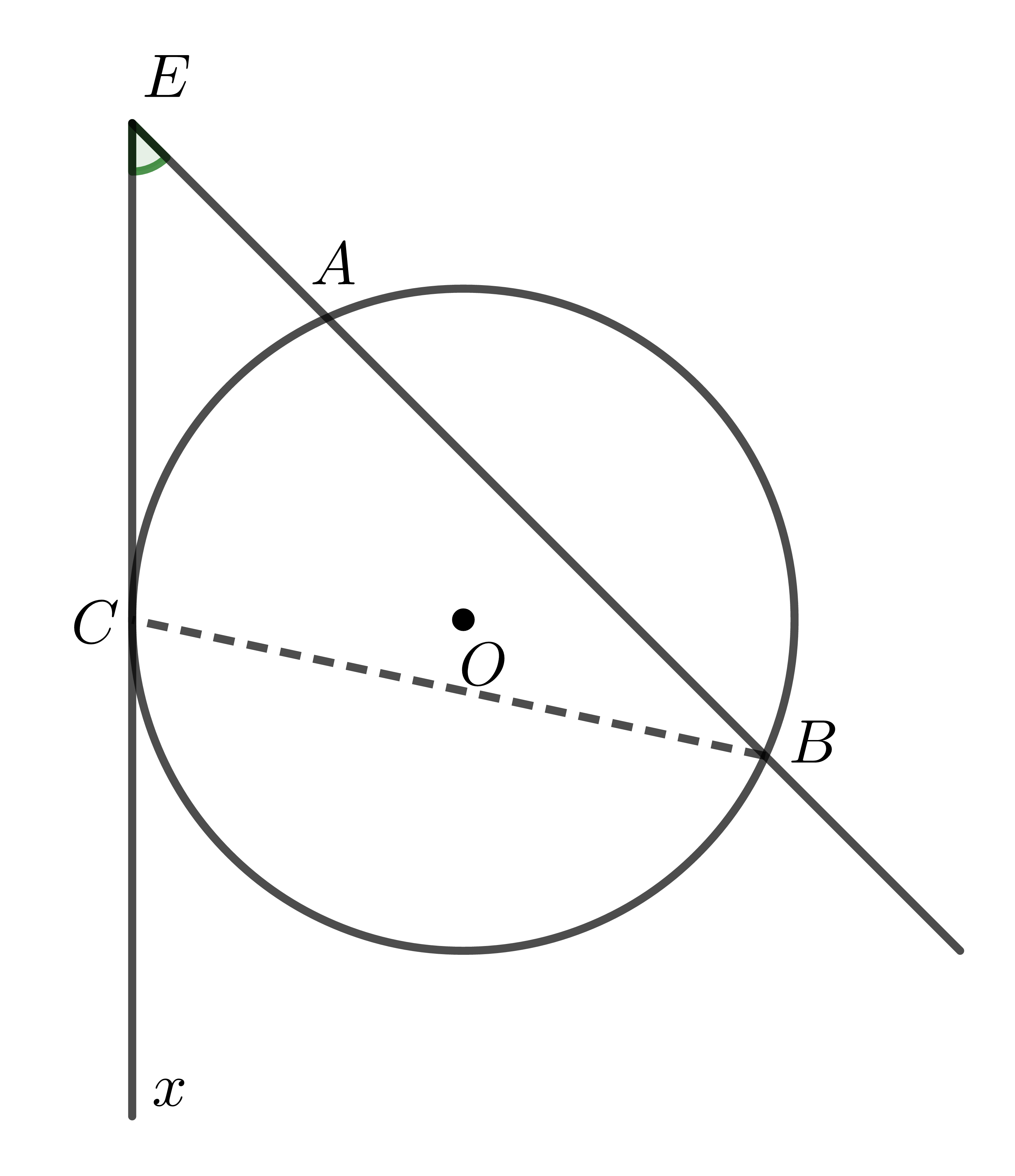
Do \(\widehat{BCx}\) là góc ngoài tam giác \(BEC\)
\(\Rightarrow\widehat{BCx}=\widehat{BEC}+\widehat{CBA}\Rightarrow\widehat{BEC}=\widehat{BCx}-\widehat{CBA}\)
Mà \(\widehat{BCx}=\dfrac{1}{2}sđ\stackrel\frown{BC}\) (tính chất góc tạo bởi tiếp tuyến và dây cung);
\(\widehat{CBA}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (tính chất góc nội tiếp)
\(\Rightarrow\widehat{BEC}=\dfrac{sđ\stackrel\frown{BC}-sđ\stackrel\frown{AC}}{2}\).
c) Trường hợp 3:
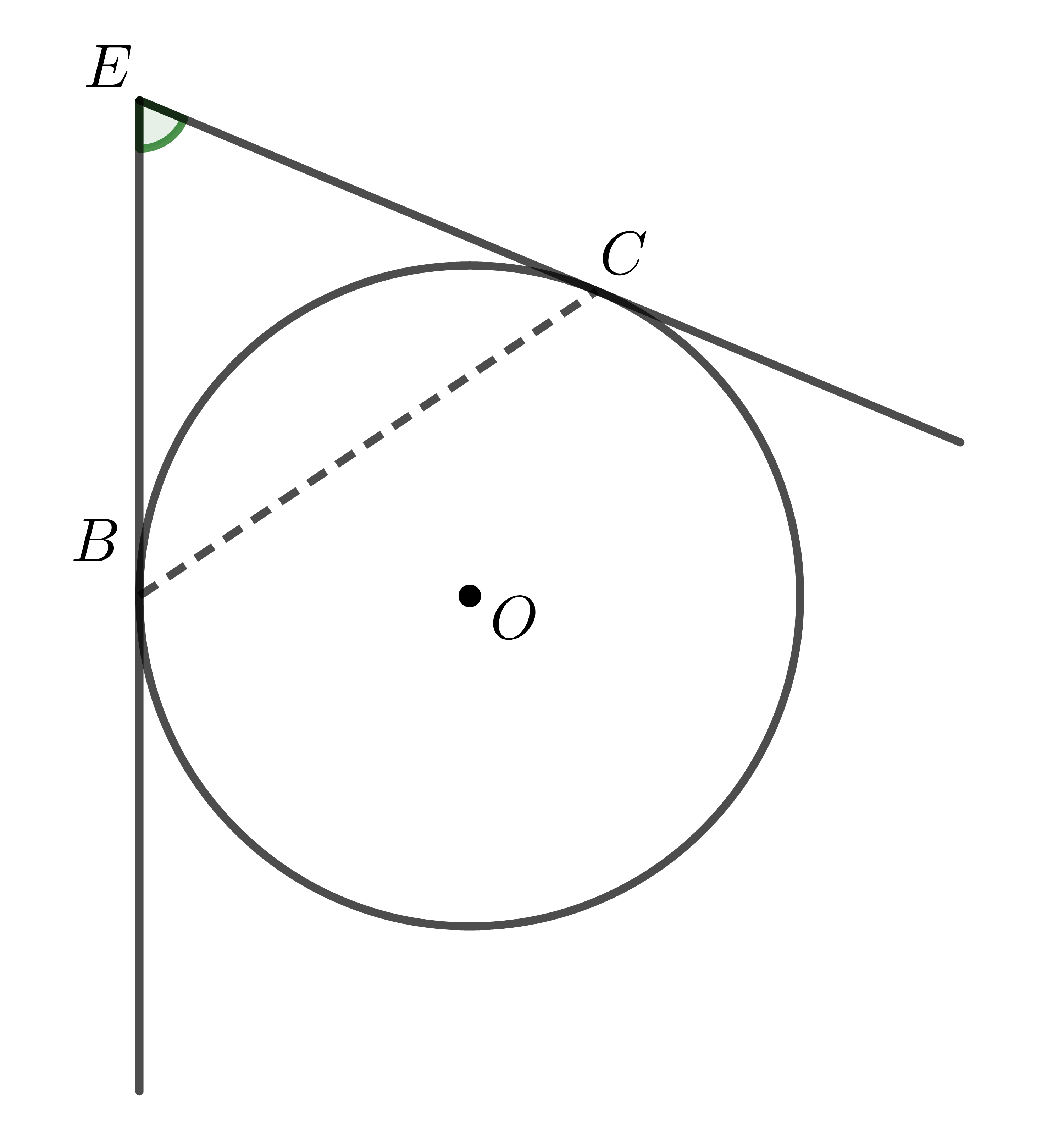
Hoàn toàn tương tự, ta dễ dàng suy ra góc \(\widehat{BEC}\) bằng nửa hiệu số đo cung lớn và cung nhỏ \(BC\).
@59541@@59574@
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn
| Nguyễn Trần Thành Đạt đã đóng góp một phiên bản khác cho bài học này (16 tháng 4 2021 lúc 19:46) | 0 lượt thích |