Bài 3: Góc nội tiếp

1. Định nghĩa

+) Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

+) Cung nằm bên trong góc được gọi là cung bị chắn.

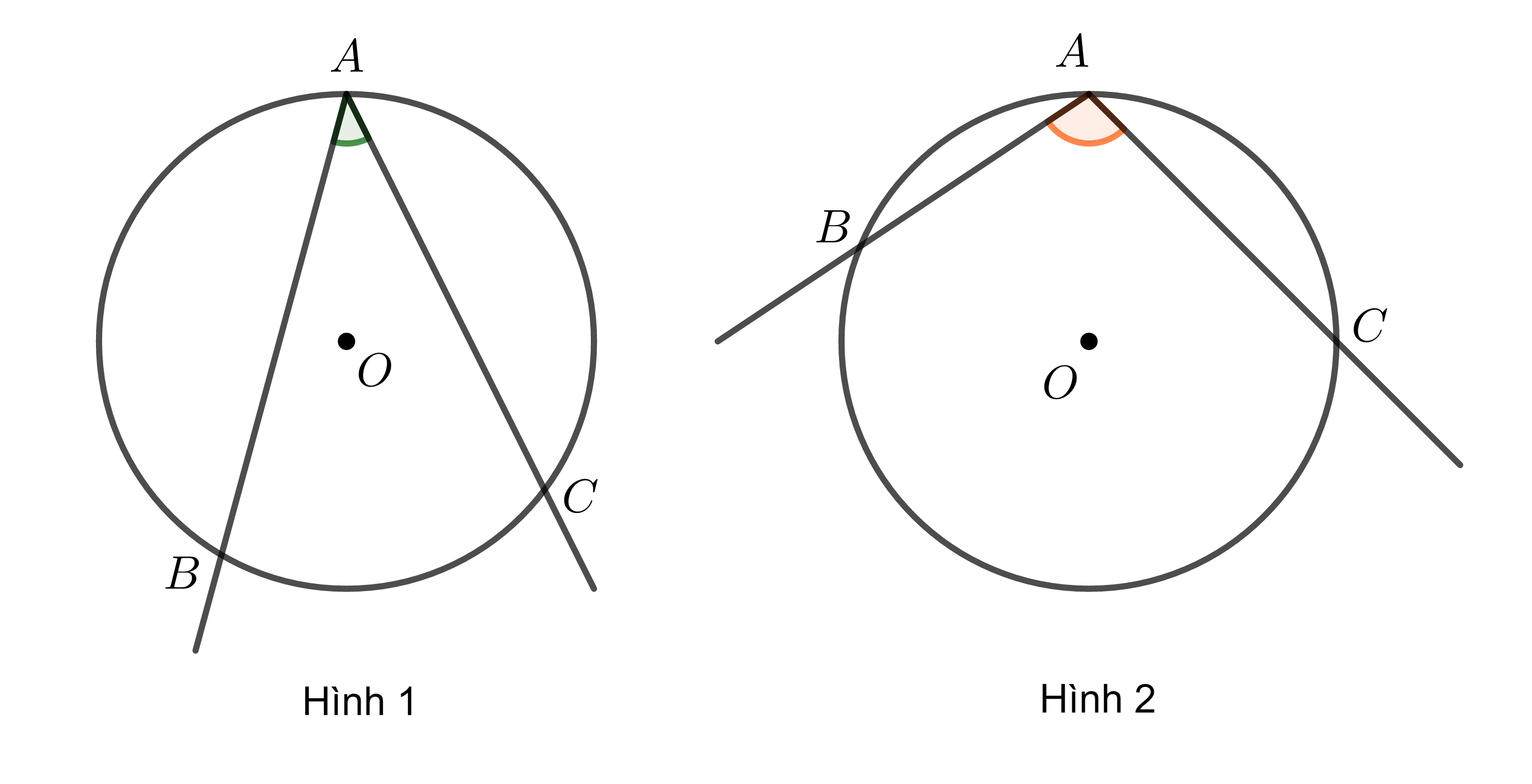
Ví dụ: Các góc trong hình 1 và hình 2 là góc nội tiếp. Trong đó:

• Cung bị chắn trong hình 1 là cung nhỏ \(BC\).
• Cung bị chắn trong hình 2 là cung lớn \(BC\).

Ví dụ: Các góc dưới đây không phải là góc nội tiếp.

2. Định lí

Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo cung bị chắn.

Ta có thể chứng minh định lí trên bằng cách chia 3 trường hợp:

a) Tâm \(O\) nằm trên một cạnh của góc \(BAC\):

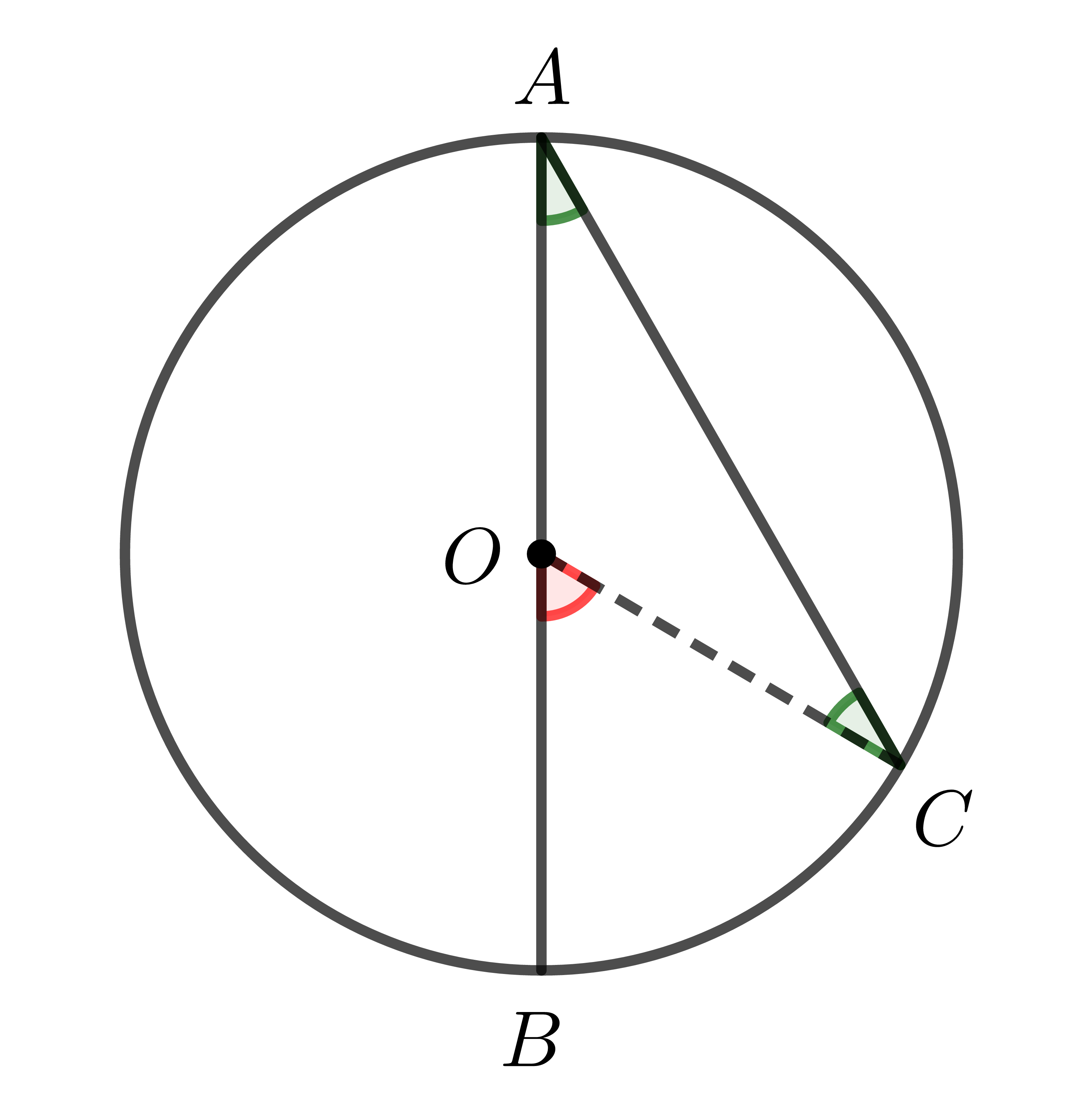
Ta có: \(\widehat{BOC}\) là góc ngoài của \(\Delta OAC\)

Theo định lí góc ngoài của tam giác: \(\widehat{BOC}=\widehat{OAC}+\widehat{OCA}\).

Mặt khác: \(OA=OC\Rightarrow\Delta OAC\) cân tại \(O\Rightarrow\widehat{OAC}=\widehat{OCA}\)

\(\Rightarrow\widehat{BOC}=2.\widehat{OAC}\Rightarrow\widehat{OAC}=\dfrac{1}{2}\widehat{BOC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\) (tính chất góc ở tâm).

b) Tâm \(O\) nằm bên trong góc \(BAC\):

Kẻ đường kính \(AD\).

Vì \(O\) nằm bên trong góc \(BAC\Rightarrow\) tia \(AO\) nằm giữa hai tia \(AB,AC\) đồng thời \(D\) nằm trên cung \(BC\).

\(\Rightarrow\left\{{}\begin{matrix}\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\\sđ\stackrel\frown{BD}+sđ\stackrel\frown{CD}=sđ\stackrel\frown{BC}\end{matrix}\right.\).

Áp dụng trường hợp a), ta có: 

\(\left\{{}\begin{matrix}\widehat{BAD}=\dfrac{1}{2}sđ\stackrel\frown{BD}\\\widehat{CAD}=\dfrac{1}{2}sđ\stackrel\frown{CD}\end{matrix}\right.\Rightarrow\widehat{BAD}+\widehat{CAD}=\dfrac{1}{2}\left(sđ\stackrel\frown{BD}+sđ\stackrel\frown{CD}\right)\)

\(\Rightarrow\widehat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\).

c) Tâm \(O\) nằm bên ngoài góc \(BAC\):

Kẻ đường kính \(AD\).

Vì \(O\) nằm bên ngoài góc \(BAC\Rightarrow\) tia \(AC\) nằm giữa hai tia \(AB,AD\) đồng thời \(C\) nằm trên cung \(BD\).

\(\Rightarrow\left\{{}\begin{matrix}\widehat{DAC}+\widehat{BAC}=\widehat{DAB}\\sđ\stackrel\frown{CD}+sđ\stackrel\frown{BC}=sđ\stackrel\frown{BD}\end{matrix}\right.\).

Áp dụng trường hợp a), ta có: 

\(\left\{{}\begin{matrix}\widehat{DAB}=\dfrac{1}{2}sđ\stackrel\frown{BD}\\\widehat{CAD}=\dfrac{1}{2}sđ\stackrel\frown{CD}\end{matrix}\right.\Rightarrow\widehat{DAB}-\widehat{CAD}=\dfrac{1}{2}\left(sđ\stackrel\frown{BD}-sđ\stackrel\frown{CD}\right)\)

\(\Rightarrow\widehat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\).

3. Hệ quả

Trong một đường tròn:

a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

c) Góc nội tiếp (nhỏ hơn hoặc bằng \(90^0\)) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.

d) Góc nội tiếp chắn nửa đường tròn là góc vuông.