Bài 2: Liên hệ giữa cung và dây

Ta dùng cụm từ "cung căng dây" hoặc "dây căng cung" để chỉ mối liên hệ giữa dây và cung có chung hai mút.

Trong một đường tròn, mỗi dây căng hai cung phân biệt. Ví dụ: trong hình dưới đây, dây \(AB\) căng cung nhỏ \(\stackrel\frown{AmB}\) và cung lớn \(\stackrel\frown{AnB}\).

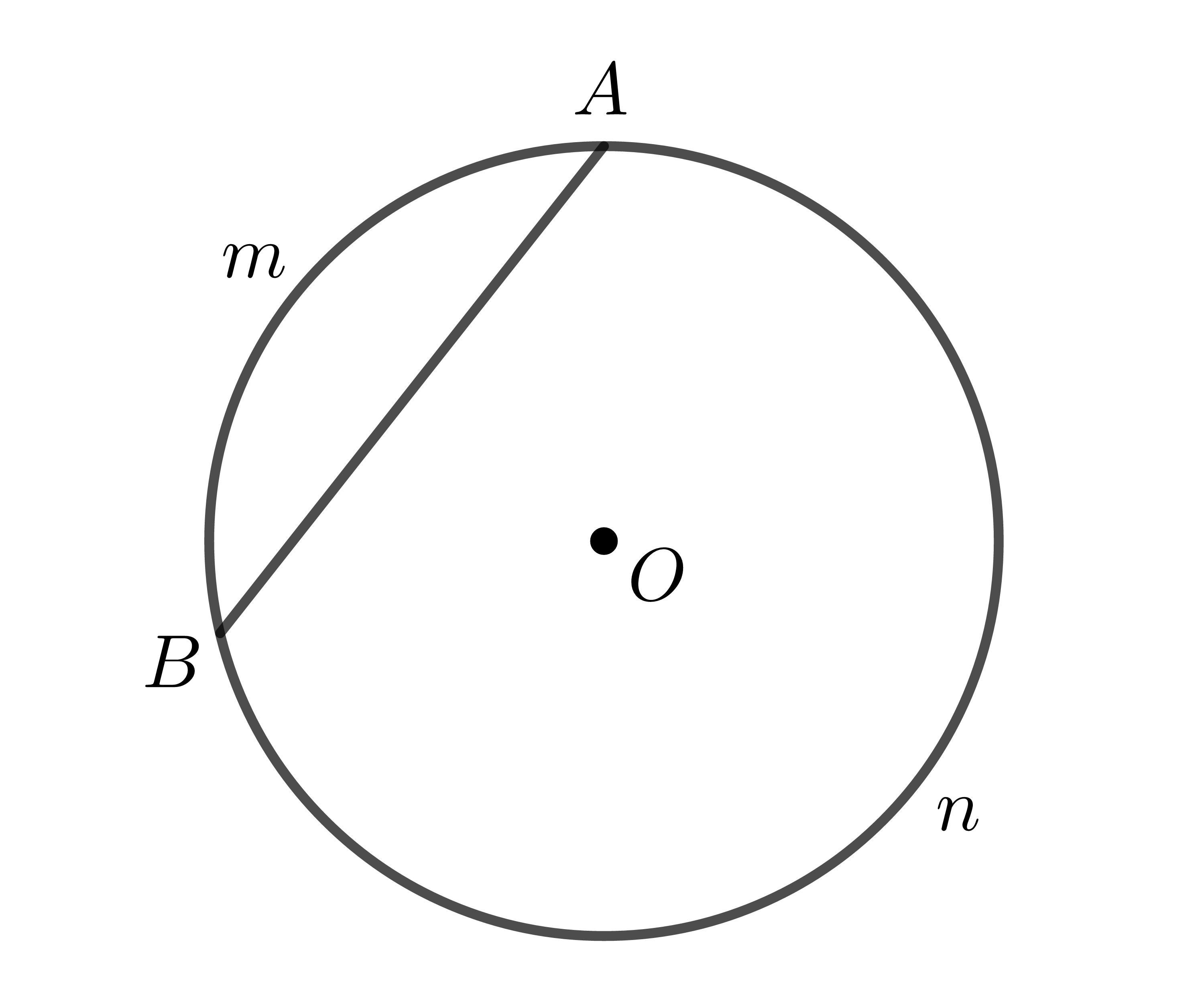
Sau đây, ta chỉ xét cung nhỏ:

1. Định lí 1

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

• Hai cung bằng nhau căng hai dây bằng nhau.
• Hai dây bằng nhau căng hai cung bằng nhau.

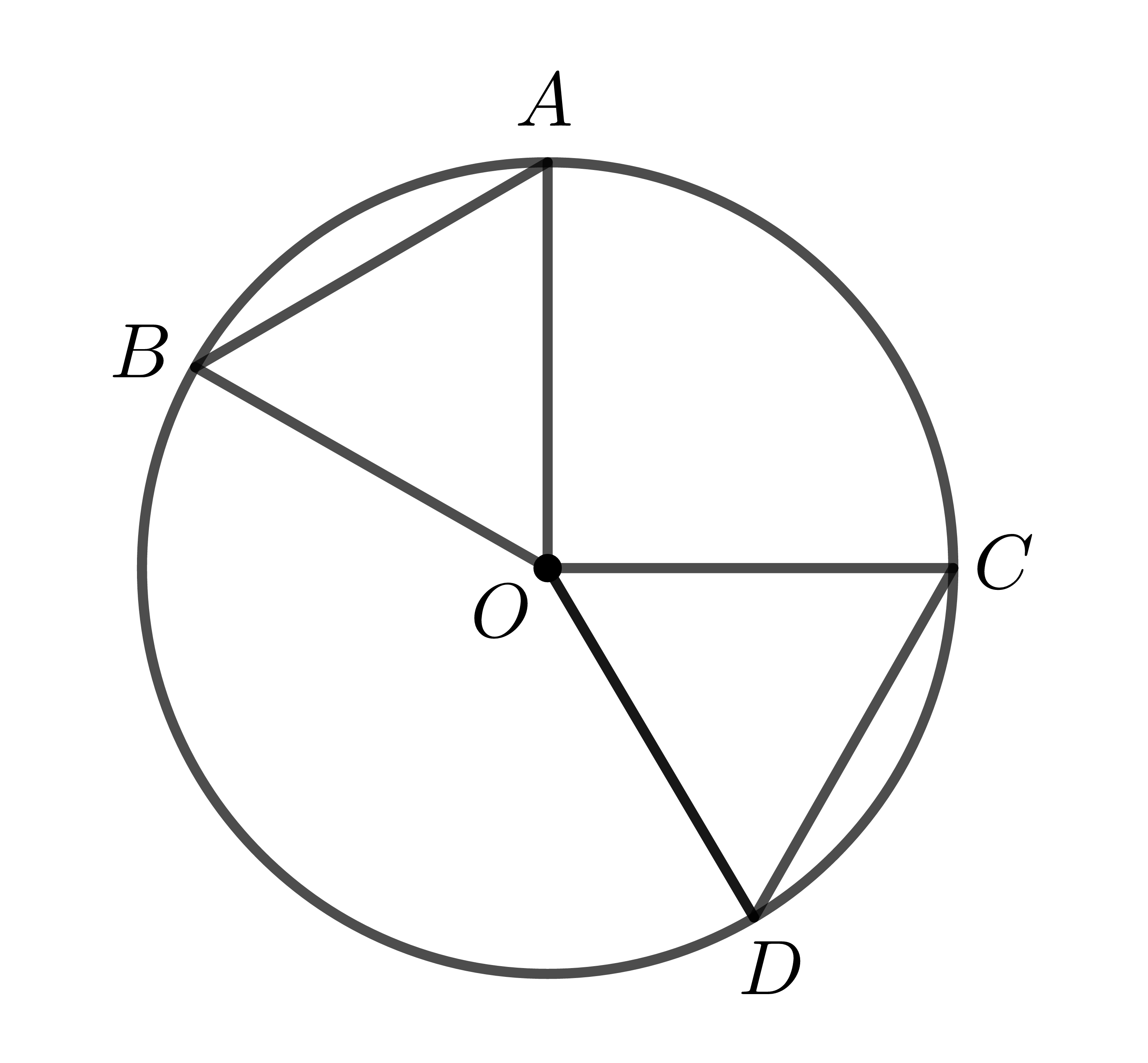
Ví dụ: trong hình trên, định lí 1 viết dưới dạng giả thiết và kết luận là:

• \(AB=CD\Rightarrow\stackrel\frown{AB}=\stackrel\frown{CD}\).
• \(\stackrel\frown{AB}=\stackrel\frown{CD}\Rightarrow AB=CD\).

Ta dễ dàng chứng minh định lí 1 như sau:

+) Trường hợp 1: \(AB=CD\)

Xét \(\Delta OAB\) và \(\Delta OCD\) có: \(\left\{{}\begin{matrix}OA=OC=R\\OB=OD=R\\AB=CD\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta OAB=\Delta OCD\) (c.c.c) \(\Rightarrow\widehat{AOB}=\widehat{COD}\Rightarrow\stackrel\frown{AB}=\stackrel\frown{CD}\).

+) Trường hợp 2: \(\stackrel\frown{AB}=\stackrel\frown{CD}\Rightarrow\widehat{AOB}=\widehat{COD}\)

Xét \(\Delta OAB\) và \(\Delta OCD\) có: \(\left\{{}\begin{matrix}OA=OC=R\\\widehat{AOB}=\widehat{COD}\\OB=OD=R\end{matrix}\right.\)

\(\Rightarrow\Delta OAB=\Delta OCD\) (c.g.c) \(\Rightarrow AB=CD\).

2. Định lí 2

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

• Cung lớn hơn căng dây lớn hơn.
• Dây lớn hơn căng cung lớn hơn.

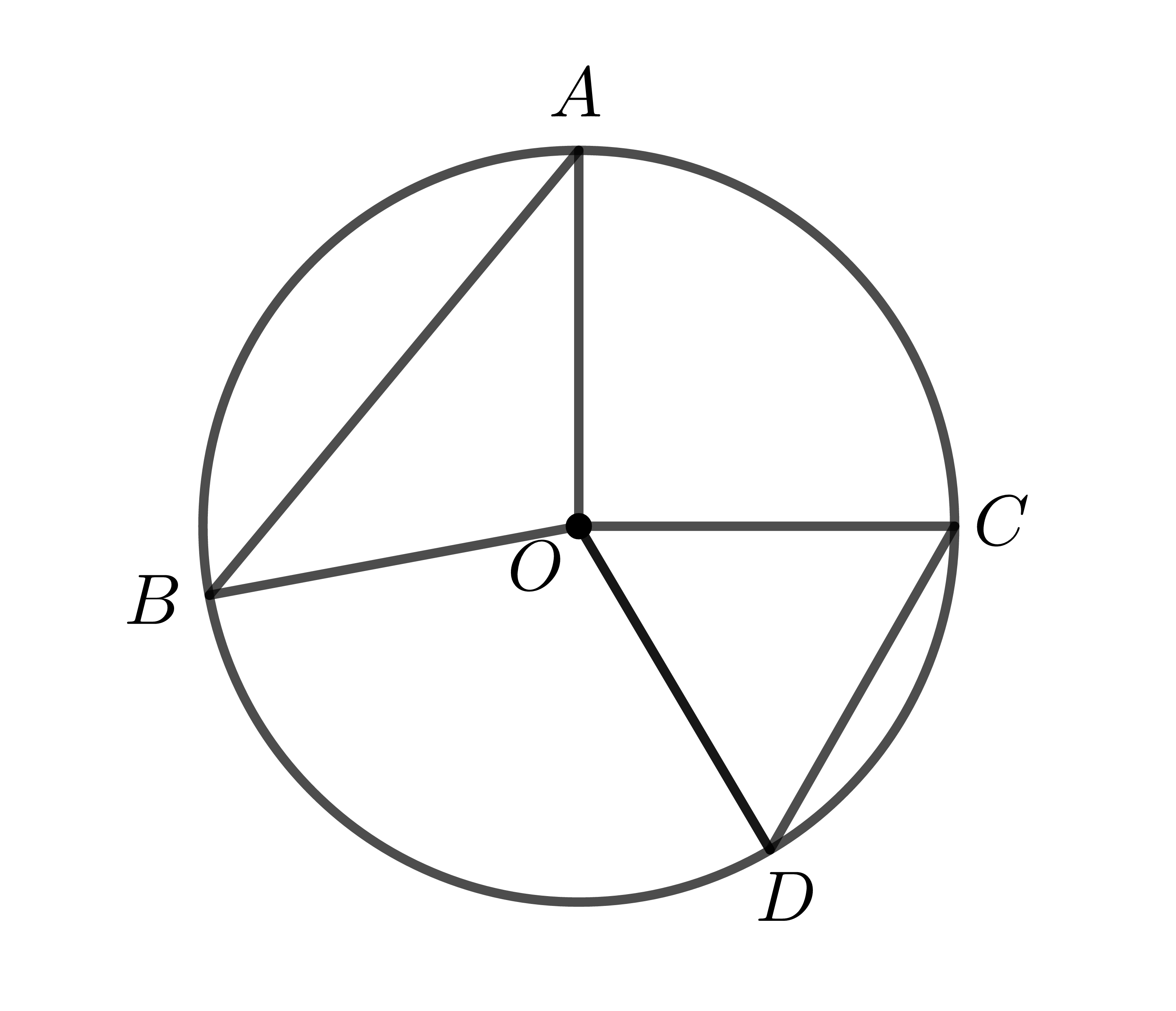
Ví dụ: Trong hình trên, định lí 2 được viết dưới dạng giả thiết và kết luận như sau:

• \(AB>CD\Rightarrow\stackrel\frown{AB}>\stackrel\frown{CD}\).
• \(\stackrel\frown{AB}>\stackrel\frown{CD}\Rightarrow AB>CD\).