Bài 2: Liên hệ giữa cung và dây

Xét (M) có

ΔAHB nội tiếp

AB là đường kính

Do đó: ΔAHB vuông tại H

=>\(\widehat{AHB}=90^0\)

Xét (N) có

ΔAHC nội tiếp

AC là đường kính

Do đó: ΔAHC vuông tại H

=>\(\widehat{AHC}=90^0\)

\(\widehat{AHB}+\widehat{AHC}=90^0+90^0=180^0\)

=>B,H,C thẳng hàng

=>AH\(\perp\)BC

Xét ΔNAM và ΔNHM có

NA=NH

AM=HM

NM chung

Do đó: ΔNAM=ΔNHM

=>\(\widehat{NAM}=\widehat{NHM}=90^0\)

Xét tứ giác AMHN có

\(\widehat{MAN}+\widehat{MHN}=90^0+90^0=180^0\)

=>AMHN là tứ giác nội tiếp

a: Xét ΔBAO vuông tại A có \(cosAOB=\dfrac{OA}{OB}=\dfrac{1}{\sqrt{2}}\)

=>\(\widehat{AOC}=45^0\)

=>\(sđ\left(OA;OC\right)=45^0\)

b: Số đo cung AC nhỏ là:

\(sđ\stackrel\frown{AC}=45^0\)

Số đo cung AC lớn là:

360⁰-45⁰=315⁰

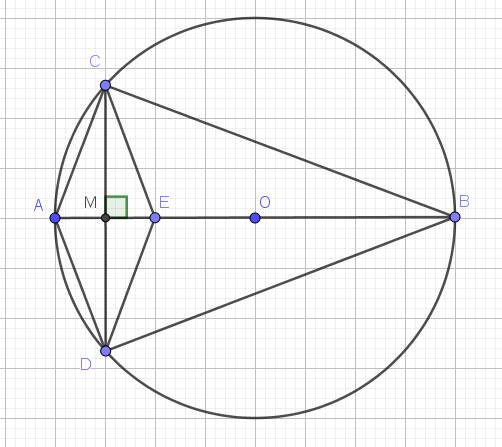
Lời giải:
a. 

Ta thấy $OC=OD=R$ nên tam giác $OCD$ cân tại $O$
$\Rightarrow$ đường cao $OM$ đồng thời là trung tuyến

$\Rightarrow M$ là trung điểm của $CD$
Tứ giác $ACED$ có 2 đường chéo $AE, CD$ cắt nhau tại trung điểm $M$ của mỗi đường nên là hình bình hành.

Mà $AE\perp CD$ nên $ACED$ là hình thoi.

b. Vì $ACED$ là hình thoi nên $AC\parallel DE(1)$

Mà $\widehat{ACB}=90^0$ (góc nội tiếp chắn nửa đường tròn - AB) 

$\Rightarrow AC\perp CB(2)$

Từ $(1); (2)\Rightarrow DE\perp CB$

Mà $BE\perp CD$ nên $E$ là trực tâm của $BCD$.

Hình vẽ:

Xét (O) có

AB,CD là dây

AB=CD

Do đó: AC//BD

Xét ΔSBD có AC//BD

nên SA/AB=SC/CD

mà AB=CD

nên SA=SC

b) Xét ΔCEB và ΔCAD có 

\(\widehat{CEB}=\widehat{CAD}\left(=180^0-\widehat{DEB}\right)\)

\(\widehat{C}\) chung

Do đó: ΔCEB\(\sim\)ΔCAD(g-g)

Suy ra: \(\dfrac{CE}{CA}=\dfrac{CB}{CD}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(CE\cdot CD=CA\cdot CB\)(đpcm)

a)Áp dụng định lí py-ta-go có:

 \(DE=\sqrt{OD^2+OE^2}=\sqrt{R^2+R^2}=\sqrt{2}R\)

Dễ chứng minh được: \(\Delta EBC\sim\Delta DAC\left(g.g\right)\)

\(\Rightarrow\dfrac{BC}{AC}=\dfrac{CE}{DC}\)\(\Rightarrow CD=\dfrac{AC.BC}{EC}=\dfrac{\left(OA+OC\right).\left(OC-OB\right)}{DC-DE}\)

\(\Leftrightarrow CD=\dfrac{8R^2}{DC-\sqrt{2}R}\)

\(\Leftrightarrow DC^2-\sqrt{2}R.DC-8R^2=0\)

\(\Leftrightarrow\left[{}\begin{matrix}CD=\dfrac{R\left(\sqrt{34}+\sqrt{2}\right)}{2}\\CD=\dfrac{R\left(-\sqrt{34}+\sqrt{2}\right)}{2}\left(ktm\right)\end{matrix}\right.\)

\(\Rightarrow CD=\dfrac{R\left(\sqrt{34}+\sqrt{2}\right)}{2}\)

Có \(EC=DC-DE=\dfrac{R\left(\sqrt{34}+\sqrt{2}\right)}{2}-\sqrt{2}R=\dfrac{R\left(\sqrt{34}-\sqrt{2}\right)}{2}\)

Vậy...

Lời giải:

Từ $O$ kẻ $OH\perp PQ$. Tam giác $OPQ$ cân tại $O$ nên đường cao $OH$ đồng thời là đường trung tuyến và phân giác.

Khi đó $H$ là trung điểm của $PQ$

$\Rightarrow PH=\frac{PQ}{2}=\frac{1}{\sqrt{2}}R$

$\sin \widehat{POH}=\frac{PH}{PO}=\frac{1}{\sqrt{2}}R:R=\frac{1}{\sqrt{2}}$

$\Rightarrow \widehat{POH}=45^0$

$\Rightarrow \widehat{POQ}=2\widehat{POH}=90^0$

Số đo cung $PQ$ là $90^0$

Hình vẽ: