Bài 8: Đường tròn nội tiếp. Đường tròn ngoại tiếp
Nội dung lý thuyết
Các phiên bản khác1. Định nghĩa
- Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác được gọi là đa giác nội tiếp đường tròn.
- Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn.
Ví dụ:
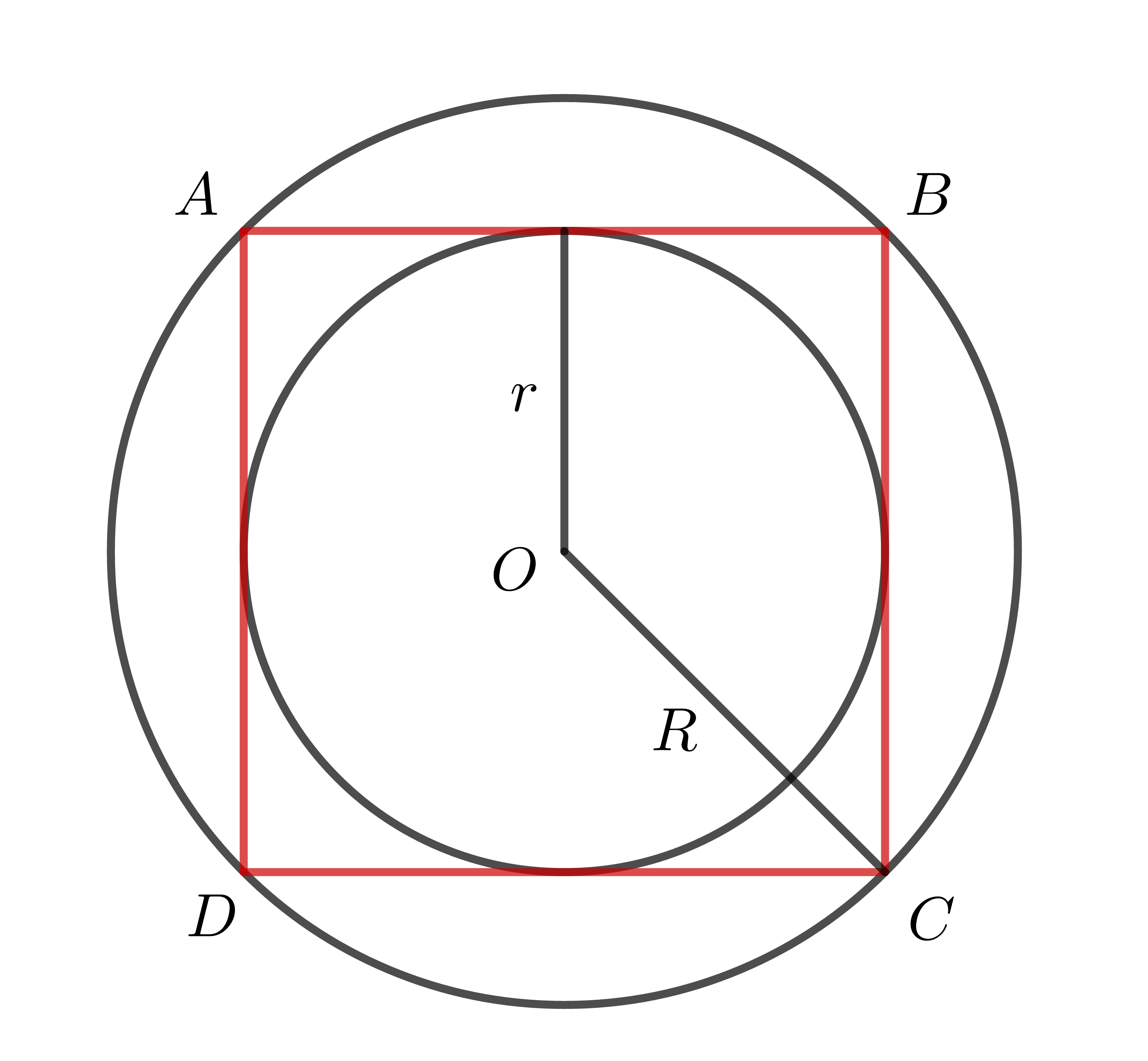
- Đường tròn \(\left(O;R\right)\) là đường tròn ngoại tiếp hình vuông \(ABCD\), hình vuông \(ABCD\) nội tiếp đường tròn \(\left(O;R\right)\).
- Đường tròn \(\left(O;r\right)\) là đường tròn nội tiếp hình vuông \(ABCD\), hình vuông \(ABCD\) ngoại tiếp đường tròn \(\left(O;r\right)\).
Nhận xét: Không phải đa giác nào cũng có đường tròn ngoại tiếp hoặc đường tròn nội tiếp.
@59827@
2. Định lí
Bất kì đa giác đều nào cũng đều có một và chỉ một đường tròn nội tiếp, có một và chỉ một đường tròn ngoại tiếp.
Nhận xét: Trong một đa giác đều, tâm của đường tròn nội tiếp trùng với tâm của đường tròn ngoại tiếp và được gọi là tâm của đa giác đều.
Ví dụ:
+) Với tam giác đều:

+) Với tứ giác đều (hình vuông):

+) Với ngũ giác đều:
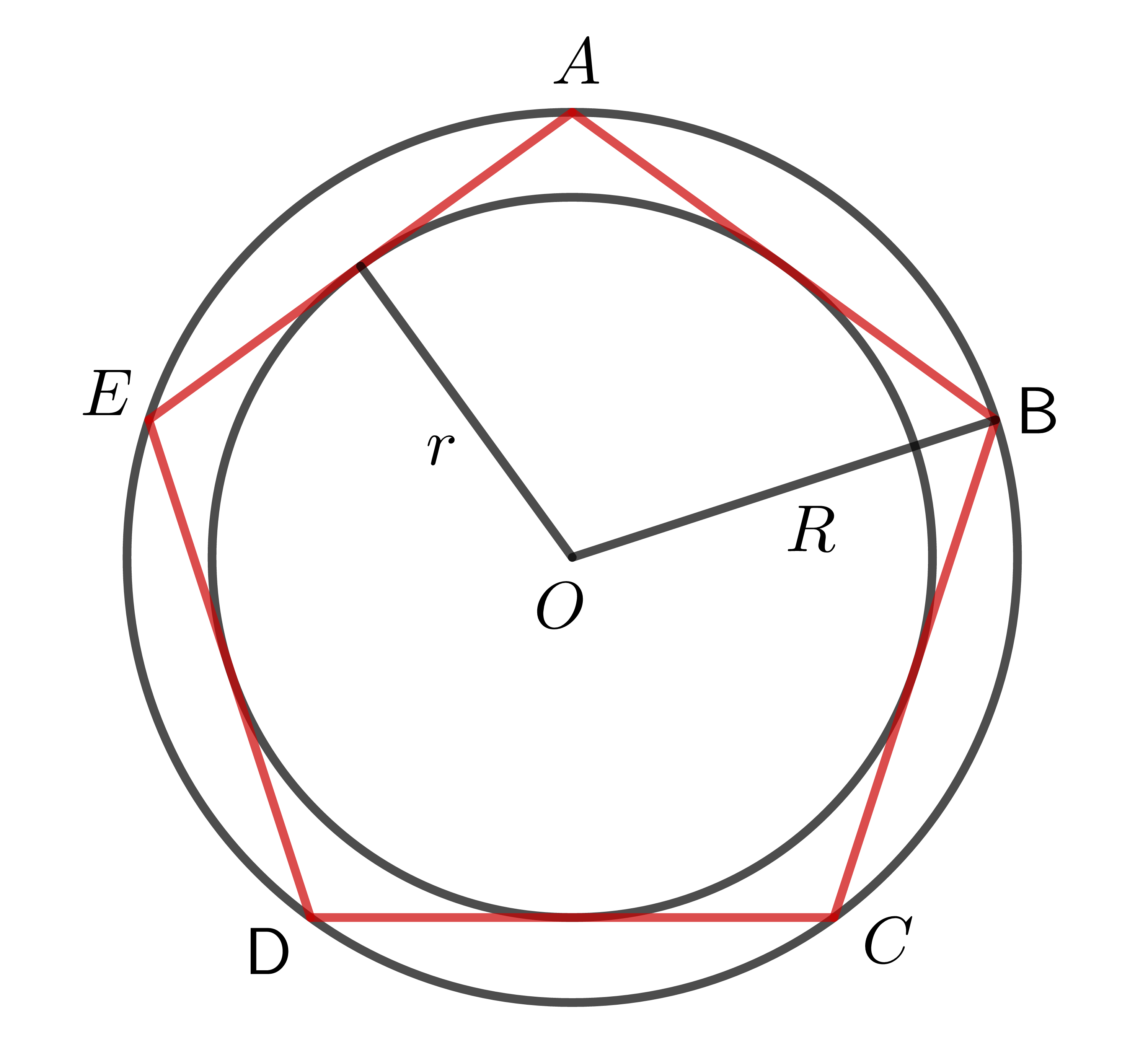
+) Với lục giác đều:

Tổng quát: Với đa giác đều \(n\) cạnh:
- Với \(n\) lẻ: Tâm của đa giác là giao điểm các đoạn thẳng nối đỉnh và trung điểm cạnh đối diện.
- Với \(n\) chẵn: Tâm của đa giác là giao điểm các đoạn thẳng nối hai đỉnh đối diện.
@59865@@59831@
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn
| Nguyễn Trần Thành Đạt đã đóng góp một phiên bản khác cho bài học này (14 tháng 7 2021 lúc 2:24) | 0 lượt thích |