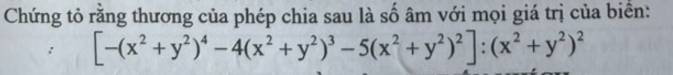Bài 11: Chia đa thức cho đơn thức

\(=\dfrac{x^3+3x^2+x-x^2-3x-1}{x^2+3x+1}=x-1\)

\(5x^3y-2x^2+3xy^2\)

\(=5x^3y-2x^2+3xy^2\)

a: =5x^2

b: =-2xz

c: \(=\dfrac{64y^9b^6}{4a^4b^2}=\dfrac{16y^9b^4}{a^4}\)

d: \(=\dfrac{3}{5}a-\dfrac{4}{5}b\)

Để -7x^n+1y^6 chia hết cho 4x^5y^n thì

n+1>=5 và 6>=n

=>4<=n<=6

=>\(n\in\left\{4;5;6\right\}\)

Sửa đề: x^4+x^3y+x^2y^2+xy^3 chia cho x^2+y^2

\(=\dfrac{x^2\left(x^2+y^2\right)+xy\left(x^2+y^2\right)}{x^2+y^2}=x^2+xy\)

d) 2(x² + 1)³ : 1/3(x² + 1)

= (2 : 1/3) . [(x² + 1)³ : (x²+ 1)]

= 6(x² + 1)²

e) 5(x - y)⁵ : 5/6(x - y)²

= (5 : 5/6) . [(x - y)⁵ : (x - y)²]

= 6(x - y)³

Bài 1:

a) (-2)⁵ : (-2)³ = (-2)² = 4

b) (-y)⁷ : (-y)³ = (-y)⁴ = y⁴

c) x¹² : (-x)¹⁰ = x¹² : x¹⁰ = x²

d) (2x)⁶ : (2x)³ = (2x)³ = 8x³

e) (-3x)⁵ : (-3x)² = (-3x)³ = -27x³

f) (xy²)⁴ : (xy²)² = (xy²)² = x²y⁴

a: \(=\left(x+2\right)^3\)

c: \(=\left(x^2+2x+4\right)^4\)

d: \(=\left(2\cdot3\right)\cdot\left[\dfrac{\left(x^2+1\right)^3}{x^2+1}\right]=6\left(x^2+1\right)^2\)

e: \(=6\left(x-y\right)^3\)

a: \(\Leftrightarrow3x^3+9x^2-5x^2-15x+18x+54+a-54⋮x+3\)

=>a-54=0

=>a=54

b: \(\Leftrightarrow x^4-x^2+ax^3-ax+x^2-1+ax+b+1⋮x^2-1\)

=>a=0 và b=-1

\(\left[-\left(x^2+y^2\right)^4-4\left(x^2+y^2\right)^3-5\left(x^2+y^2\right)^2\right]:\left(x^2+y^2\right)^2\\ =\left[-\left(x^2+y^2\right)^4:\left(x^2+y^2\right)^2\right]+\left[-4\left(x^2+y^2\right)^3:\left(x^2+y^2\right)^2\right]+\left[-5\left(x^2+y^2\right)^2:\left(x^2+y^2\right)^2\right]\\ =-\left(x^2+y^2\right)^2-4\left(x^2+y^2\right)-5\left(x^2+y^2\right)\left(ĐPCM\right)\)