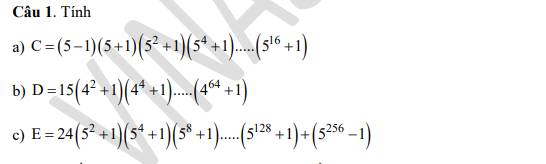a) \(C=\left(5-1\right)\left(5+1\right)\left(5^2+1\right)\left(5^4+1\right)...\left(5^{16}+1\right)\)
\(C=\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)...\left(5^{16}+1\right)\)
\(C=\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(C=\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(C=\left(5^{16}-1\right)\left(5^{16}+1\right)\)
\(C=5^{32}-1\)
b) \(D=15\cdot\left(4^2+1\right)\left(4^4+1\right)...\left(4^{64}+1\right)\)
\(D=\left(4^2-1\right)\left(4^2+1\right)\left(4^4+1\right)...\left(4^{64}+1\right)\)
\(D=\left(4^4-1\right)\left(4^4+1\right)\left(4^8+1\right)...\left(4^{64}+1\right)\)
.....
\(D=\left(4^{32}-1\right)\left(4^{32}+1\right)\left(4^{64}+1\right)\)
\(D=\left(4^{64}+1\right)\left(4^{64}-1\right)\)
\(D=4^{128}-1\)
c) \(E=24\left(5^2+1\right)\left(5^4+1\right)...\left(5^{256}+1\right)\)
\(E=\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)...\left(5^{256}+1\right)\)
\(E=\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)...\left(5^{256}+1\right)\)
.....
\(E=\left(5^{128}-1\right)\left(5^{128}+1\right)\left(5^{256}+1\right)\)
\(E=\left(5^{256}-1\right)\left(5^{256}+1\right)\)
\(E=5^{512}-1\)
a: \(C=\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(=\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(=\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(=\left(5^{16}-1\right)\left(5^{16}+1\right)=5^{32}-1\)
b: \(D=\left(4^2-1\right)\left(4^2+1\right)\left(4^4+1\right)\cdot...\cdot\left(4^{64}+1\right)\)
\(=\left(4^4-1\right)\left(4^4+1\right)\left(4^8+1\right)\left(4^{16}+1\right)\left(4^{32}+1\right)\left(4^{64}+1\right)\)
\(=\left(4^8-1\right)\left(4^8+1\right)\left(4^{16}+1\right)\left(4^{32}+1\right)\left(4^{64}+1\right)\)
\(=\left(4^{16}-1\right)\left(4^{16}+1\right)\left(4^{32}+1\right)\left(4^{64}+1\right)\)
\(=\left(4^{32}-1\right)\left(4^{32}+1\right)\left(4^{64}+1\right)\)
\(=\left(4^{64}-1\right)\left(4^{64}+1\right)=4^{128}-1\)
c: \(E=\left(5^2-1\right)\left(5^2+1\right)\cdot...\cdot\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\cdot...\cdot\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^8-1\right)\left(5^8+1\right)\cdot...\cdot\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{16}-1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)\left(5^{64}+1\right)\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{32}-1\right)\left(5^{32}+1\right)\left(5^{64}+1\right)\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{64}-1\right)\left(5^{64}+1\right)\left(5^{128}+1\right)+5^{256}-1\)
\(=5^{256}-1+5^{256}-1=2\cdot5^{256}-2\)
a) C = (5 - 1)(5 + 1)(5² + 1)(5⁴ + 1)...(5¹⁶ + 1)
= (5² - 1)(5² + 1)(5⁴ + 1)...(5¹⁶ + 1)
= (5⁴ - 1)(5⁴ + 1)...(5¹⁶ + 1)
= (5⁸ - 1)...(5¹⁶ + 1)
= 5³² - 1
b) D = 15(4² + 1)(4⁴ + 1)...(4⁶⁴ + 1)
= (4² - 1)(4² + 1)(4⁴ + 1)...(4⁶⁴ + 1)
= (4⁴ - 1)(4⁴ + 1)...(4⁴⁶ + 1)
= (4¹⁶ - 1)...(4⁶⁴ + 1)
= 4¹²⁸ - 1
c) E = 24(5² + 1)(5⁴ + 1)...(5¹²⁸ + 1)(5²⁵⁶ + 1)
= (5² - 1)(5² + 1)(5⁴ + 1)...(5¹²⁸ + 1)(5²⁵⁶ + 1)
= (5⁴ - 1)(5⁴ + 1)...(5¹²⁸ + 1)(5²⁵⁶ + 1)
= (5⁸ - 1)...(5¹²⁸ + 1)(5²⁵⁶ + 1)
= (5²⁵⁶ - 1)(5²⁵⁶ + 1)
= 5⁵¹² - 1