giúp em câu 3b với hình ak
HN
Những câu hỏi liên quan
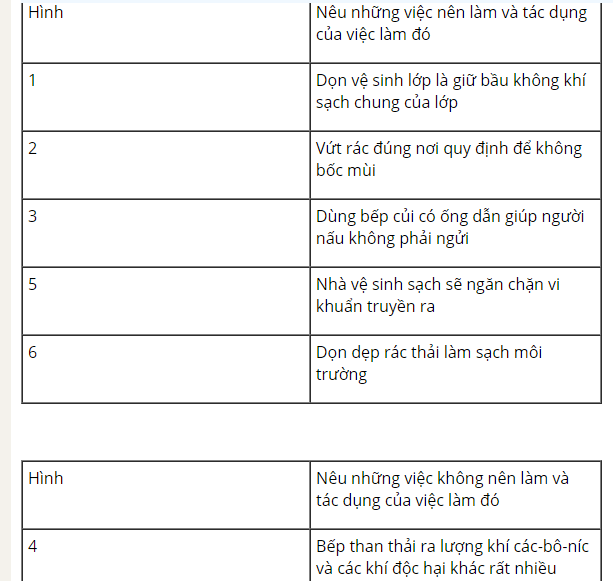
Quan sát hình 1,2,3,4,5,6,7 giúp em câu 3a và 3b

giúp em cách làm câu 3b với ạ em cảm ơn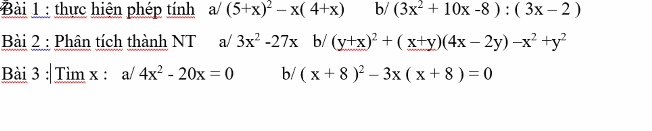
Bài 3:
\(b,\Leftrightarrow\left(x+8\right)\left(x+8-3x\right)=0\\ \Leftrightarrow\left(x+8\right)\left(8-2x\right)=0\\ \Leftrightarrow2\left(4-x\right)\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giúp em câu 3b với 4 ạ cảm ơn mọi người
Bài 3:
b: Ta có: \(\sqrt{x^2-2x+1}=\left|x-2\right|\)
\(\Leftrightarrow\left|x-1\right|=\left|x-2\right|\)
\(\Leftrightarrow x-1=2-x\)
\(\Leftrightarrow2x=3\)
hay \(x=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Bài 4: ĐK: x>0
a) \(B=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}+1-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(\Leftrightarrow B=\dfrac{\sqrt{x}\left[\left(\sqrt{x}\right)^3+1\right]}{x-\sqrt{x}+1}+1-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}\)
\(\Leftrightarrow B=\dfrac{\sqrt{x}.\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-2\sqrt{x}-1\)
\(\Leftrightarrow B=\sqrt{x}.\left(\sqrt{x}+1\right)-2\sqrt{x}=x+\sqrt{x}-2\sqrt{x}\)
\(\Leftrightarrow B=x-\sqrt{x}\)
Vậy với x>0 thì \(B=x-\sqrt{x}\)
b) Ta có: \(B=2\)
\(\Leftrightarrow x-\sqrt{x}=2\)
\(\Leftrightarrow x-\sqrt{x}-2=0\)
\(\Leftrightarrow x-2\sqrt{x}+\sqrt{x}-2=0\)
\(\Leftrightarrow\sqrt{x}.\left(\sqrt{x}-2\right)+\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)=0\)
Do \(\sqrt{x}+1>0\) nên, ta suy ra:
\(\sqrt{x}-2=0\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\) \(\left(TMĐK\right)\)
Vậy \(x=4\) thì \(B=2\)
Đúng 0
Bình luận (0)
Bài 4:
a: Ta có: \(B=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+1\)
\(=\sqrt{x}\left(\sqrt{x}+1\right)-\left(2\sqrt{x}+1\right)+1\)
\(=x+\sqrt{x}-2\sqrt{x}-1+1\)
\(=x-\sqrt{x}\)
b: Để B=2 thì \(x-\sqrt{x}-2=0\)
\(\Leftrightarrow\sqrt{x}-2=0\)
hay x=4
Đúng 0
Bình luận (0)
 giải giúp em câu 3b đi ạ
giải giúp em câu 3b đi ạ
3b:
ĐKXĐ: \(x\in R\)
\(\sqrt{x^2+2x+4}+\left(x-1\right)\left(x+3\right)+1=0\)
=>\(\sqrt{x^2+2x+4}+x^2+2x-3+1=0\)
=>\(\sqrt{x^2+2x+4}+x^2+2x-2=0\)
=>\(x^2+2x+4+\sqrt{x^2+2x+4}-6=0\)
=>\(\left(\sqrt{x^2+2x+4}\right)^2+3\sqrt{x^2+2x+4}-2\sqrt{x^2+2x+4}-6=0\)
=>\(\left(\sqrt{x^2+2x+4}+3\right)\left(\sqrt{x^2+2x+4}-2\right)=0\)
=>\(\sqrt{x^2+2x+4}-2=0\)
=>\(\sqrt{x^2+2x+4}=2\)
=>\(x^2+2x+4=4\)
=>\(x^2+2x=0\)
=>x(x+2)=0
=>\(\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giúp em câu 4 ak
Giúp em câu này với!!!
Cho tam giác abc nhọn (AB<AC) ,3 đường cao AK,BE,CF cắt nhau tại H. Cho KH=2,KB=3,KC=4 tính độ dài AK?
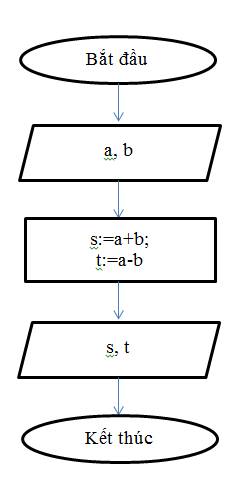
em hãy mô tả thuật toán tính tổng ,hiệu hai số a và b bằng sơ đồ khối ai giúp mik câu này với ak
Xem chi tiết

giusp em câu 3b, với ạ
Ptr hoành độ của `(P)` và `(d)` là:
`x^2=-5x-3m+1`
`<=>x^2+5x+3m-1=0` `(1)`
Để `(P)` cắt `(d)` tại `2` điểm phân biệt thì ptr `(1)` có `2` nghiệm phân biệt
`=>\Delta > 0`
`<=>5^2-4(3m-1) > 0`
`<=>25-12m+4 > 0`
`<=>m < 29/12`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=-5),(x_1.x_2=c/a=3m-1):}`
Ta có: `[x_1 ^2]/[x_2]-[x_2 ^2]/[x_1]+3=75/[x_1.x_2]`
`<=>[x_1 ^3-x_2 ^3]/[x_1.x_2]+[3x_1.x_2]/[x_1.x_2]=75/[x_1.x_2]`
`=>(x_1-x_2)(x_1 ^2+x_1.x_2+x_2 ^2)+3x_1.x_2=75`
`<=>(x_1-x_2)[(x_1+x_2)^2-x_1.x_2]+3x_1.x_2=75`
`<=>(x_1-x_2)[(-5)^2-3m+1]+3(3m-1)=75`
`<=>(x_1-x_2)(26-3m)=78-9m`
`<=>x_1-x_2=[3(26-3m)]/[26-3m]`
`<=>x_1-x_2=3`
Kết hợp với `x_1+x_2=-5`
Giải hệ `=>{(x_1=-1),(x_2=-4):}`
Thay vào `x_1.x_2=3m-1` có:
`-1.(-4)=3m-1`
`<=>m=5/3` (t/m)
Đúng 1
Bình luận (1)
Giải chi tiết giúp mình câu 2 với câu 3b và c với huhu. Cảm ơn mng ạ
b.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x-\dfrac{1}{2}sin2x=-cosx\)
\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{6}\right)=cos\left(x+\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{6}=x+\pi+k2\pi\\2x+\dfrac{\pi}{6}=-x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{6}+k2\pi\\x=-\dfrac{7\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
c.
\(\Leftrightarrow2cos4x.sin3x=2sin4x.cos4x\)
\(\Leftrightarrow cos4x\left(sin4x-sin3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\sin4x=sin3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\pi}{2}+k\pi\\4x=3x+k2\pi\\4x=\pi-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=k2\pi\\x=\dfrac{\pi}{7}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
Đúng 2
Bình luận (1)
2.
\(f\left(x\right)=\dfrac{1}{2}-\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x-5\)
\(=-\dfrac{9}{2}-\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)\)
\(=-\dfrac{9}{2}-cos\left(2x-\dfrac{\pi}{3}\right)\)
Do \(-1\le-cos\left(2x-\dfrac{\pi}{3}\right)\le1\Rightarrow-\dfrac{11}{2}\le y\le-\dfrac{7}{2}\)
\(y_{min}=-\dfrac{11}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
\(y_{max}=-\dfrac{7}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\Rightarrow x=\dfrac{2\pi}{3}+k\pi\)
Đúng 2
Bình luận (1)